Глава 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ
Виды общественных явлений и формы
Связей между ними
Статистическое изучение взаимосвязей исходит из предположения о всеобщей связи и взаимодействия явлений общественной жизни. Взаимосвязь и взаимообусловленность наблюдается при рассмотрении показателей работы любого предприятия. Например, повышение производительности труда влечёт за собой снижение себестоимости единицы продукции. Те общественные явления (или их отдельные признаки), которые оказывают влияние на другие и обуславливают их изменения, называют факторными. Те общественные явления (или их отдельные признаки), которые изменяются под влияние факторных, называются результативными (производительность труда – факторный, а себестоимость продукции – результативный показатель).
По характеру зависимости явлений различают функциональную (полную) и корреляционную (неполную) связи между ними. Функциональной называется связь, для которой каждому значению факторного показателя соответствует вполне определённое значение результативного показателя. Функциональные зависимости находят широкое применение в точных науках. Что же касается общественных явлений, то они складываются под влиянием множества факторов, которые, в свою очередь, взаимодействуют друг с другом. Причём, точно известно, в какой мере каждый из них влияет на величину явления. Такого рода связи называются корреляционными. В корреляционных связях между причиной и следствием нет полного соответствия, а наблюдается лишь известное соотношение. Каждому значению факторного показателя соответствует при этом ряд значений результативного признака. Однако, и это очень важно, с изменением значений факторного признака меняется средняя величина результативного признака.
Связи между явлениями можно классифицировать и по другим признакам:
· По направлению (прямые, обратные).
· По аналитическому выражению (линейные, нелинейные).
· По тесноте связи или степени приближения её к функциональной (сильные, слабые).
Связь двух признаков называется парной корреляцией, влияние нескольких факторных признаков на результативный признак – множественной корреляцией.
Методы изучения взаимосвязей между явлениями и характеризующими их признаками
Изучение взаимосвязей – важнейшая познавательная задача статистики, которую она решает с помощью особых методов. Помимо аналитических группировок к этим методам относятся: метод сопоставления параллельных рядов, балансовый метод и методы, основанные на положениях и теоремах математической статистики (корреляционный, факторный, дисперсионный).
Сущность метода сопоставления параллельных рядов состоит в том, что полученные в результате сводки и обработки материала располагаются параллельными рядами либо по признаку пространства, либо по признаку времени. Совместное изучение такого рода рядов даёт возможность проследить соотношение и направление изменений сопоставляемых признаков изучаемого явления. Важным условием получения достоверных результатов использования этого метода является предварительное обнаружение причинно-следственной связи между изучаемыми признаками.
Сущность балансового метода заключается в характеристике ресурсов изучаемого явления и их распространения. Простейшим балансом является баланс материальных ресурсов на предприятии, а именно: остаток на начало анализируемого периода + поступление = расход + остаток на конец анализируемого периода. Ясно, что поскольку поступление и расход материальных ресурсов должны находиться в определённом соответствии (например, в равенстве), постольку между правой и левой частями (элементами) приведённого выше баланса должна быть выдержана определённая пропорциональность. Характеристика этой пропорциональности и должна быть найдена в результате балансовых построений. Возможности в характеристике взаимосвязей и пропорций значительно расширяются, если поступление в балансе разделить по источникам (поставщикам), а расход – по назначениям (покупателям). В этом случае баланс покажет взаимосвязь не только между поступлением, расходом и остатком в пределах предприятия, но и между данным предприятием и другими предприятиями, одни из которых снабжают его материальными ресурсами, а другие – потребляют его продукцию. С помощью балансового метода можно изучать оборот не только материальных, но и трудовых ресурсов, денежных средств, основных фондов.
В связи с указанными особенностями корреляционных зависимостей перед методами изучения взаимосвязей, основанными на положениях математической статистики, возникает две задачи:
1). обнаружить эту зависимость на фактическом материале и установить аналитическое выражение связи;
2). измерить тесноту связи.
Для решения первой задачи необходимо осуществить выбор факторных и результативных показателей, собрать соответствующий фактический материал, обработать его с помощью графических построений.
Вторая задача решается расчётом коэффициентов корреляции, параметров регрессии.
Продемонстрируем метод корреляционного анализа на примере установления тесноты связи между показателями электровооружённости труда и производительности труда, если имеется следующий фактический материал:
| № п/п | Показатели | |||||||
| Х | Коэффициент роста электровооружённости | 1,00 | 1,04 | 1,55 | 1,62 | 1,79 | 2,06 | 2,15 |
| Y | Коэффициент роста производительности труда | 1,00 | 1,17 | 2,03 | 2,21 | 2,44 | 2,60 | 2,70 |
Теперь для решения первой задачи осталось необходимым определить какой из двух анализируемых показателей является факторным (Х), а какой – результативным (Y), а затем представить связь между ними графически. Очевидным является, что из двух анализируемых показателей электровооружённость труда является факторным, а его производительность – результативным показателем. Поэтому в системе прямоугольных координат значения первого будем откладывать по оси абсцисс, а значения второго – по оси ординат (см. рис.3).
y
x
Рис. 3 Значения факторного и результативного показателей
Как видно из рис. 3, значения результативного показателя расположены не по прямой, соединяющей крайние его значения, а в виде «облачка», вытянутого вдоль этой прямой. Существуют специальные приёмы, позволяющие находить тот вид аналитического выражения связи (прямая, гипербола, парабола и т.д.), который наилучшим образом соответствует функциональной зависимости. Простейший вид корреляционной зависимости выражается уравнением y=a+bx, где применительно к рассматриваемому нами примеру у – коэффициент роста производительности труда; х – коэффициент роста электровооружённости; а b– параметры уравнения.
Измерение тесноты связи (определение значений а, в) между двумя показателями (х, у), связанными линейной зависимостью, возможно в результате решения следующей систему уравнений:
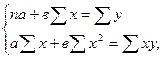
где n– число наблюдений (в нашем случае n=7).
Для решения системы уравнений построим таблицу, в которой наряду с исходными данными поместим результаты всех необходимых промежуточных расчётов, а именно:
| п/п | x | y | xy | x 
| y
|
| 1,04 1,55 1,62 1,79 2,06 2,15 | 1,17 2,03 2,21 2,44 2,60 2,70 | 1,217 3,146 3,580 4,368 5,356 5,805 | 1,08 2,40 2,62 3,20 4,24 4,62 | 1,37 4,12 4,88 5,95 6,76 7,29 | |
| Итого | 11,21 ( )
| 14,15 ( )
| 24,472 ( )
| 19,16 ( )
| 31,37 ( )
|
Тогда система уравнений с двумя неизвестными (а,в) приобретает вид:
а её решение позволяет определить конкретное их значение: а = -0,45;
в = 1,542. Следовательно, у = 1,542х – 0,45. Подставляя в это уравнение (так называемое уравнение регрессии) конкретные значения х, получаем расчётное значение функции - 
:
| X | 1,00 | 1,09 | 1,55 | 1,62 | 1,79 | 2,06 | 2,15 |
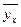
| 1,09 | 1,15 | 1,94 | 2,04 | 2,21 | 2,73 | 2,87 |
Сравнивая значения «y» и «
» видим, что они близки, но не совпадают друг с другом. Это означает, что на темпы роста производительности труда влияют не только на темпы роста его энерговооружённости, но и другие факторы, которые оказались неучтёнными. Количественной характеристикой тесноты связи между исследуемой парой показателей является коэффициент корреляции между ними r 
, значения которого изменяются в пределах от
(– 1) до (+1) и тем больше по абсолютной величине, чем меньше искажающее влияние неучтённых факторов.
Исследование статистической зависимости результативного признака от нескольких факторных признаков предполагает, что в качестве последних будут отобраны наиболее существенные из них. Введение большого числа факторов осложняет решение задачи. Непродуманное же их сокращение приводит к тому, что уравнение не будет воспроизводить исследуемое явление. В уравнение нельзя вводить фактор, находящиеся между собой в функциональной или близкой к функциональной связи. При введении их в уравнение наблюдается явление коллинеарности (если факторов два) или мультиколлинеарности (если факторов более двух). Выявление вышеназванных явлений осуществляется с помощью расчёта коэффициентов корреляции между факторами. Если величина коэффициентов корреляции между факторами будет больше или равна 0,8, то при дальнейшем исследовании один из таких факторов отбрасывается. В такой процедуре не будет необходимости при использовании факторного анализа. Факторный анализ отличается тем, что, не опираясь на заранее заданный перечень факторов, он помогает обнаружить наиболее важные из них. Например, экономист непосредственно наблюдает множество различных показателей статистического учёта деятельности предприятия, чтобы выявить закономерности, влияющие на рост производительности труда (образовательный уровень рабочих, коэффициент сменности оборудования, электровооружённость труда, возраст оборудования и т.п.). Так или иначе, все факторы, отражаемые этими показателями, воздействуют на производительность труда. При этом многие из них связаны между собой, отражая с разных сторон те же, по существу, явления. С помощью приёмов факторного анализа этих связей удаётся обнаружить, что на самом деле решающее влияние на рост производительности труда оказывают лишь несколько обобщающих факторов (например, размер предприятия, уровень организации труда, характер продукции), непосредственно не наблюдавшихся при исследовании. Задача состоит, следовательно, в том, чтобы выявить скрытые обобщающие факторы. Выявленные факторы позволяют строить уравнение множественной регрессии с относительно небольшим числом коэффициентов.
Дисперсионный анализ призван выявить влияние отдельных факторов на результат эксперимента. Суть этого метода состоит в том, что совокупность наблюдений группируют по факторному признаку, находя среднюю результата и дисперсию по каждой группе. Затем определяют общую дисперсию и вычисляют, какая доля её зависит от условий, общих для всех групп, какая – от исследуемого фактора, а какая – от случайных причин. И наконец, с помощью специального критерия, определяют настолько существенны различия между группами наблюдений и, следовательно, можно ли считать ощутимым влияние тех или иных факторов. По существу дисперсионный анализ служит предварительным этапом регрессионного анализа статистических данных, позволяющих выделить относительно небольшое, но достаточное для целей исследования количество параметров регрессии.
Библиографический список
Социально - экономическая статистика: практикум/ под ред. В.Н. Салина, Е.П. Шпаковской. – М.: Финансы и статистика, 2006.
Практикум по социально – экономической статистике/ Л.П. Чижова. – М.: Дашков и К, 2003.
Практикум по общей теории статистики/ М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова. – М.: Финансы и статистика, 2004.
Теория статистики/ Л.И. Ниворожкина, Т.В. Чернова. – Ростов-на-Дону: Феникс, 2005.
Статистика/ под ред. И.И. Елесеевой. – М.: Проспект, 2006.
Микроэкономическая статистика/ под ред. С.Д. Ильенковой. – М.: Финансы и статистика, 2004.
Статистика/ под ред. И.И. Елесеевой. – М.: Кнорус, 2006.
