Прежде чем приступить к работе, необходимо ознакомиться с введением потеме: "ТЕПЛОВЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ".
Цель работы: определить линейный и объемный коэффициенты расширения металлического стержня при помощи оптического длиннометра.
Формулы, необходимые для вычислений
Коэффициент линейного расширения, который характеризует удлинение тела при данной температуре, определяется формулой (1). На практике для характеристики теплового расширения тел часто ограничиваются определением среднего коэффициента линейного расширения
 
| (21.1) |
где l и l 1 – длина тела, соответствующая температуре t и t 1, l 0 – длина при стандартной температуре 0 или 20°C.
Коэффициент объемного расширения определяется
| (21.2) |
Легко показать, что для монокристаллов, обладающих кубической симметрией и для поликристаллов
| (21.3) |
Монокристаллы в отличие от поликристаллов, обладают анизотропией теплового расширения, т.е. коэффициент линейного расширения для различных направлений внутри кристалла будет иметь различные значения.
При измерении коэффициента αнеобходимо обеспечить наибольшую точность определения весьма малых смещений. Приборы для измерения теплового расширения называются дилатометрами (по-гречески - измеритель расширения).
Наиболее точное измерение коэффициентов объемного расширения производится методом рентгеноструктурного анализа - измерением смещения дифракционных пятен.
Описание экспериментальной установки. Установка состоит из термостата с контактным термометром, вертикального оптического длинномера иводяной бани, в которую помещается исследуемый стержень. Для более точного определения температуры к работе прилагаются дополнительные термометры с точность до 0,1°С.
| Рис. 21.1 |
Для термостатирования и регулирования температуры на интервале от комнатной температуры до 100°С применяется термостат ТС-15м. При помощи контактного термометра, закрепленного в термостате, задается требуемое значение температуры. Нагретая до заданной температуры вода при помощи насоса, имеющегося в термостате, прогоняется по шлангам через водяную баню, в которую помещен рабочий стержень. Отсчет удлинения рабочего стержня производится с помощью вертикального оптического длинномера ИЗВ-1. Это прибор высокого класса точности, которая достигается при помощи оптических методов отсчета.
Длинномер (рис. 21.1) имеет следующие основные характеристики: точность измерений в пределах до 100 мм по аттестату шкалы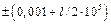 
мм, цена наименьшего деления окулярного микрометра 0,001 мм при подъеме измерительной головки до 250 мм.
Исследуемый стержень закрепляется на столике длинномера 1, наконечник измерительного стержня 2 опускается до контакта со стержнем, отсчет длины производится по спиральному окулярному микрометру. Винтом 5 можно перемещать вверх или вниз окуляр для установления начала отсчета, в процессе эксперимента подающий винт 5 вращать нельзя.
На основную шкалу внутри цилиндрического стержня 6 нанесено 100 делений, расстояние между ними равно одному миллиметру. С помощью осветительного устройства штрихи и цифры шкалы проецируются в поле зрения отсчетного микроскопа 3.
Изображение миллиметровой шкалы совмещается в поле зрения микроскопа с помещенными в окуляре двумя дополнительными шкалами (рис. 21.2): прямолинейной неподвижной шкалой, имеющей 10 делений по 0,1 мм и круговой вращающейся шкалой, нанесенной на одной пластинке с архимедовой спиралью. Расстояние между двумя витками спирали Архимеда равно цене деления прямолинейной шкалы (0,1 мм), угол поворота отсчитывается по круговой шкале, имеющей 100 делений, следовательно, цена ее деления 0,001 мм. Начало круговой шкалы (отсчет "0") соответствует такому положению спирали, когда каждый ее виток совпадает с соответствующей риской прямолинейной шкалы. Витки спирали делают двойными, так как совместить риску шкалы с серединой между двумя витками можно точнее, чем с 
винтом простой спирали.
| Рис. 21.2 |
Отсчет по спиральному микроскопу. В поле зрения отсчетного микроскопа (см. рис. 21.2) одновременно видны: два - три штриха миллиметровой шкалы, обозначенных крупными цифрами, например, 11, 12, 13, десять двойных витков спирали, неподвижная шкала десятых долей миллиметра спирального микроскопа с делениями от 0 до 10, круговая шкала отсчета сотых долей миллиметра. На рис. 21.2 штрих 12 миллиметровой шкалы установился между рисками 2 и 3 прямолинейной шкалы. Очевидно, отсчет будет 12 плюс отрезок от штриха 12 до нулевого штриха шкалы десятых долей миллиметра спирального микрометра. В этом отрезке число десятых долей миллиметра будет равно числу двойных витков спирали, прошедших через штрих 12. Таких витков два, значит, отрезок равен 0,2 мм. Для того чтобы произвести отсчет сотых и тысячных долей миллиметра, необходимо предварительно маховичком 4 (см. рис.21.1) подвести двойной виток спирали с номером 3 так, чтобы миллиметровый штрих 12, находящийся в зоне двойных витков, оказался точно посередине между линиями витка с номером 3 (см. рис. 21.2). Затем по круговой шкале отсчитать сотые и тысячные доли миллиметра. Индексом для отсчета по этой шкале служит вертикальный указатель, цена деления круговой шкалы, как уже отмечалось, равна 0,001 мм. Как видно из рисунка 21.2, указатель остановился между штрихами 72 и 73 шкалы. Значит, в отрезке содержится 0,072 мм. Часть интервала между штрихами 72 и 73 определить на глаз. Она примерно равна 0,5 деления круговой шкалы. Итак, окончательный отсчет будет 12,2725 мм, а именно 12 мм (жирная цифра основной шкалы) + 0,2 мм (отсчет по вертикальной шкале) + 0,072 мм (показание указателя круговой шкалы) + 0,0005 мм (отсчет на глаз по положению указателя между 72 и 73 делениями круговой шкалы).
Преимуществом спирального микрометра является отсутствие мертвого хода и одинаковость расстояния от глаз всех цифр, исключающая необходимость различной аккомодации глаза [5].
Порядок выполнения работы
1. Измерительную головку опустить до соприкосновения с рабочим стержнем. Включить осветитель и произвести установку длинномера. По шкале и по спиральному микрометру отсчитать положение измерительной головки при начальной (комнатной) температуре
2. Включить термостат.
3. Включить насос, прогоняющий воду из термостата через водяную баню, служащую для обогревания рабочего стержня.
Измерения удлинения рабочего стержня производить в интервале температур от комнатной до 95°С через 5 или 10°С (по указанию преподавателя). Требуемые температуры выставлять с помощью контактного термометра. Отсчет температуры производить при помощи дополнительного ртутного термометра с точностью до 0,1°С. Прежде чем приступить к снятию показаний, необходимо убедиться в установлении теплового равновесия между стержнем и термостатируемой жидкостью.
Установилось или нет тепловое равновесие, можно проверить следующим образом. При срабатывании контактного термометра записать показания длиннометра. Через 2 - 3 минуты провести второе измерение при той же температуре. Совпадение второго показания с предыдущим указывает на наступление теплового равновесия. В противном случае необходимо выждать еще некоторое время (2 - 3 минуты). Для расчетов берется значение последнего измерения.
Составить таблицу измерений:
| 1. | t 0C | l,мм | Δ t = x | Δ l = y |
| 2. | t 1 | l 1 | t 2- t 1 | l 2- l 1 |
| 3. | t 2 | l 2 | t 3- t 1 | l 3- l 1 |
| 4. | t 3 | l 3 | t 4- t 1 | l 4- l 1 |
| 5. | t 4 | l 4 | t 5- t 1 | l5 - l 1 |
| . . | . . . | . . . | . . . | . . . |
Визучаемом интервале температур коэффициент линейного расширения с достаточной точностью можно считать постоянным. Следовательно, если выражение (21.1) переписать в виде
|
то получим уравнение, выражающее линейную зависимость Δ l от Δ t, тангенс угла наклона этой прямой - a равен
|
где l 0 - полная длина исследуемого стержня. Применяя метод наименьших квадратов(6), следует найти величину а и ее доверительные границы Δ a. Соответственно α и Δα будут равны
|
Содержание отчета
1. График зависимости удлинения стержня от температуры.
2.Таблица наблюдений и расчетов по МНК тангенса угла наклона прямой в зависимости Δ l = f( Δ t)
3. Значение величины α и доверительные границы для неё, рассчитанные по МНК.
4. Коэффициент объемного расширения β для образца, рассчитанный по формуле (21.3).
Вопросы
1. Какие силы действуют между частицами твердого тела, как они зависят от расстояния?
2. Чем объясняется расширение тел при нагревании?
3. Какова связь между коэффициентом линейного и объемного расширения?
