Пусть известны результаты двух серий независимых испытаний: в первой серии проведено п 1 опытов, и событие А появилось т 1 раз; во второй серии из п 2 опытов событие А появилось т 2 раз. Обозначим неизвестную вероятность появления события А в одном опыте первой серии через р 1, а во второй серии – через р 2. Требуется проверить при уровне значимости α нулевую гипотезу о равенстве этих вероятностей: Но: р 1 = р 2.
В качестве критерия выбирается нормированная нормально распределенная случайная величина
.
Наблюдаемое значение критерия вычисляется по формуле:
.
Построение критической области:
а) при конкурирующей гипотезе Н 1: р 1 ≠ р 2 uкр определяется из равенства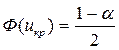 
, и двусторонняя критическая область задается неравенством | U | > uкр.
б) при конкурирующей гипотезе Н 1: р 1 > р 2 uкр для правосторонней крити-ческой области находится из условия 
, и вид критической области: U > uкр.
в) при конкурирующей гипотезе Но: р 1 < р 2 левосторонняя критическая область имеет вид U < – uкр, где uкр находится по формуле из пункта б).
Пример. В серии из 20 независимых испытаний событие А появилось 8 раз, в серии из 15 испытаний – 7 раз. При уровне значимости α = 0,05 проверяется
нулевая гипотеза Но: р 1 = р 2 при конкурирующей гипотезе Но: р 1 < р 2.
Решение.
Критическая область – левосторонняя, 
следова-
тельно, икр = 1,645, и критическая область имеет вид U < - 1,645. Вычислим инабл = 
Uнабл > – uкр, следовательно, гипотеза принимается, и можно считать, что вероятность события А в обеих сериях испытаний одинакова.
Проверка гипотезы о значимости выборочного
Коэффициента корреляции
Пусть имеется выборка объема п из нормально распределенной двумерной генеральной совокупности (Х, Y), и по ней найден выборочный коэффициент корреляции rB ≠ 0. Требуется при заданном уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции:
Ho: rГ = 0 при конкурирующей гипотезе Н 1: rГ ≠ 0. Критерием является случайная величина
,
имеющая при справедливости нулевой гипотезы распределение Стьюдента с k = n – 2 степенями свободы. Критическая область при заданном виде конку-рирующей гипотезы является двусторонней и задается неравенством | T | > tкр, где tкр (α, k) находится по таблице критических точек распределения Стьюдента.
Пример. По выборке объема п = 150, извлеченной из нормально распреде-ленной двумерной генеральной совокупности, вычислен выборочный коэффициент корреляции rB = - 0,37. Проверим при уровне значимости α = 0,01 нулевую гипотезу Ho: rГ = 0 о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе Н 1: rГ ≠ 0.
Решение.
Критическая точка tкр (0,01; 150) = 2,58. Вычислим наблюдаемое значение критерия: 
Поскольку | Tнабл | > tкр, нулевая гипо-теза отвергается, то есть Х и Y коррелированны.
Критерий согласия Пирсона
Критерием согласия называется критерий проверки гипотезы о предпола-гаемом законе неизвестного распределения.
Пусть по выборке объема п получено эмпирическое распределение:
| Варианты xi | x 1 | x 2 | ... | xs |
| Частоты ni | n 1 | n 2 | ... | ns |
С помощью критерия Пирсона можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормаль-ном, показательном и др.) Для этого в предположении о конкретном виде распределения вычисляются теоретические частоты 
, и в качестве крите-рия выбирается случайная величина
,
имеющая закон распределения χ 2 с числом степеней свободы k = s – 1 – r, где s – число частичных интервалов выборки, r – число параметров предполагаемого распределения. Критическая область выбирается правосто-ронней, и граница ее при заданном уровне значимости α 
находит-ся по таблице критических точек распределения χ 2.
Теоретические частоты вычисляются для заданного закона распределения как количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределе-ния, параметры которого совпадают с их точечными оценками по выборке, а именно:
а) для проверки гипотезы о нормальном законе распределения = п ∙ Рi, где п – объем выборки, 
xi и xi + 1 – левая и правая границы i -го интервала, 
- выборочное среднее, s – исправленное среднее квадратическое отклонение. Поскольку нормальное распределение характеризуется двумя параметрами, число степеней свободы k = n – 3;
б) для проверки гипотезы о показательном распределении генеральной совокупности в качестве оценки параметра λ принимается 
. Тогда теоретические частоты = п ∙ Рi, 
. Показательное распреде-ление определяется одним параметром, поэтому число степеней свободы k = n – 2;
в) для проверки гипотезы о равномерном распределении генеральной совокупности концы интервала, в котором наблюдались возможные
значения Х, оцениваются по формулам:
Тогда плотность веро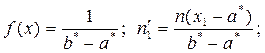ятности 
Число степеней свободы k = n – 3, так как равномерное распределение оценивается двумя параметрами.
Пример. Для выборки, интервальный статистический ряд которой имеет вид
| Номер интервала | Границы интервала | Эмпирические частоты |
| 2 – 5 | ||
| 5 – 8 | ||
| 8 – 11 | ||
| 11 – 14 | ||
| 14 – 17 | ||
| 17 – 20 |
проверить при уровне значимости α = 0,05 гипотезу о:
а) показательном; б) равномерном; в) нормальном
законе распределения генеральной совокупности с помощью критерия Пирсона.
Решение.
Объем выборки п = 70. Будем считать вариантами середины частичных интервалов: х 1 = 3,5, х 2 = 6,5,…, х 6 = 18,5.
Найдем = 11,43; σВ = 4,03; s = 4,05.
а) Вычислим теоретические частоты в предположении о показательном распределении генеральной совокупности при 
аналогично 
Наблюдаемое значение критерия 
Критическая точка χ 2(0,05;4)=9,5; 
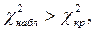и гипотеза о показательном распределении отклоняется.
б) Для равномерного распределения 
теоретические частоты: 
Наблюдаемое значение критерия 
Критическая точка 
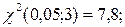
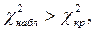и гипотеза о равномерном распределении отклоняется.
в) Теоретические частоты для нормального распределения:
Так же вычисляют-ся 
Наблюдаемое значение критерия 
Критическая точка 
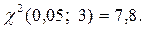Поскольку 
гипотеза о нормальном распределе-нии генеральной совокупности принимается.
