, (9)
где CV – молярная теплоемкость газа при постоянном объеме.
2. Изобарический процесс происходит при постоянном давлении р = const.
Первый закон термодинамики для изобарического процесса записывается так:
(10)
т.е. все члены сохраняются.
В этом случае количество теплоты, необходимое для нагревания газа находится так
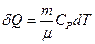, (11)
где Ср – молярная теплоемкость газа при постоянном давлении.
Учитывая, что изменение внутренней энергии газа вычисляется по формуле (9), а работа может быть найдена из уравнения Менделеева-Клапейрона:
(12)
первый закон термодинамики можно переписать в виде:
(13)
Из последнего выражения находится связь молярных теплоемкостей Ср и CV
, (14)
где R = 8,31 Дж/(моль × К) – универсальная газовая постоянная.
Из уравнения (14), называемого уравнением Майэра, видно, что СР > CV.
Большее значение СР по сравнению с CV объясняется тем, что для нагревания 1 моля газа на 1 К при постоянном давлении требуется подвести больше тепла, чем для нагревания при постоянном объеме, так как часть тепла при изобарном нагревании должна пойти на совершение работы.
3. Изотермический процесс происходит при постоянной температуре T = const.
Первый закон термодинамики для изотермического процесса записывается так:
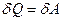(15)
т.е. все тепло, подведенное к газу, идет только на совершение им работы, так как изменение внутренней энергии, ввиду постоянства температуры, равно нулю.
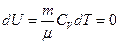(16)
Теплоемкость в изотермическом процессе равна СТ = ¥.
Связь теплоемкости газов с числом степеней свободы его молекул
Согласно классической теории теплоемкостей газов молярные теплоемкости газов СР и CV могут быть определены, если известно число степеней свободы i молекул данного вида. Под числом степеней свободы подразумевают число независимых координат, которые необходимо задать для того, чтобы полностью определить положение тела или частицы тела в пространстве. У одноатомных газов, молекулы которых состоят из одного атома (аргон, гелий), движение каждой молекулы описывается тремя независимыми координатами x, y, z, то есть каждая молекула обладает тремя степенями свободы.
Молекула двухатомного газа (водород, азот, кислород, окись углерода и др.) обладает пятью степеней свободы, т.к. кроме трех поступательных движений, она может совершать еще два вращательных движения вокруг
двух взаимно перпендикулярных осей, составляющих прямой угол с линией, соединяющей оба атома. Если расстояние между атомами в двухатомной молекуле может меняться (квазиупругая молекула), т.е. атомы совершают колебательное движение, то такая молекула обладает шестью степенями свободы. Три степени свободы соответствуют поступательному, две – вращательному и одна – колебательному движению атомов молекулы.
Молекулы трехатомного газа (если центры трех атомов не расположены на одной прямой) и многоатомных газов обладают шестью степенями свободы: из них три относятся к поступательному движению и три – к вращательному движению.
В основе классической теории теплоемкости лежит закон равномерного распределения энергии по степеням свободы, позволяющий определить среднее значение энергии одной молекулы.
Средняя кинетическая энергия поступательного движения молекулы одноатомного идеального газа пропорциональна его абсолютной температуре
(17)
Отсюда следует, это энергия, приходящаяся на одну степень свободы поступательного движения, равна 
. Следовательно, молекула, обладающая i степенями свободы, имеет энергию
,
где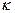 
– постоянная Больцмана ( 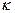= 1,38 × 10-23 Дж/К).
Тогда внутренняя энергия одного моля идеального газа будет
, (18)
где NA – число молекул в моле идеального газа.
Дифференцируя это выражение по температуре, получим для молярной теплоемкости идеального газа при постоянном объеме
(19)
Подставляя значение CV в уравнение Майера (8), находим выражение для молярной теплоемкости СР
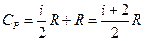(20)
В ряде случаев необходимо знать отношение теплоемкостей СР и CV, которое будет
(21)
Из формул (11) и (12) видно, что по классической теории теплоемкость газов не должна зависеть от температуры.
Адиабатный процесс
Адиабатным называют процесс изменения состояния газа, происходящий без теплообмена с окружающей средой. Всякий, быстро протекающий процесс в газе, практически адиабатен. Адиабатный процесс имеет место в двигателях внутреннего сгорания, холодильных установках и т.д.
При адиабатном процессе 
, и уравнение первого начала термодинамики принимает вид:
(22)
Для одного моля газа можно записать
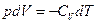(23)
Таким образом, при адиабатном процессе работа может совершаться только за счет изменения запаса внутренней энергии системы. Следовательно, при адиабатном расширении температура газа должна уменьшаться (dT < 0), а при адиабатном сжатии температура должна повышаться (dT > 0). При адиабатном сжатии - расширении изменяются все параметры состояния газа (р, V, T). Увеличение температуры газа при адиабатном сжатии происходит вследствие того, что работа, затрачиваемая извне на сжатие газа, целиком идет на увеличение его внутренней энергии.
Подставив в уравнение (23) значение 
из уравнения Менделеева – Клапейрона и разделив переменные, запишем его в виде
или 
, (24)
где
,
Интегрируя и потенцируя выражение (24), получим:
или 
(25)
Уравнения (25) являются уравнениями адиабатного процесса и называются уравнениями Пуассона. Поскольку показатель степени адиабаты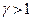 
, кривая адиабатного процесса (адиабата) идет круче, чем изотерма 
.
Описание установки и метода измерений
Для определения отношения теплоемкостей используется метод, основанный на адиабатном расширении газа.
Воздух, заключенный в сосуд, последовательно проходит через три состояния (рис. 1). Первое состояние характеризуется параметрами р1V1T1. Второе состояние газа определяется параметрами р2V2T2. Третьему состоянию соответствуют параметры р3V2T1. Из первого во второе состояние газ переходит путем адиабатного расширения. Из второго в третье состояние газ переходит изохорно.
В адиабатном процессе 1-2 давление и объем газа по уравнению Пуассона связаны следующими соотношениями:
(26)
Начальное и конечное состояния газа характеризуются одной и той же температурой, поэтому на основании закона Бойля-Мариотта получаем
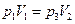(27)
Решая уравнения (26) и (27) относительно 
, получим
(28)
 |
Рис. 1
Так как давление р1, р2, р3 отличаются друг от друга незначительно, при приближенном вычислении разности логарифмов в формуле (28) можно заменить разностями самих чисел
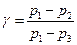(29)
В проводимом эксперименте давление р2 равно атмосферному, а давления р1 и р3 превышают атмосферное давление р2 на величины, определяемые высотами столбов жидкости в манометре h1 и h2 соответственно. С учетом этого формула (29) для расчета значения 
примет вид
(30)
Измерительная установка для определения 
состоит из стеклянного баллона большой емкости 1, крана 3, открытого жидкостного манометра 4 и ручного нагнетательного насоса 2 (рис. 2).
 |
Рис. 2
Если в баллон при открытом кране 3 накачивается воздух, то давление его в баллоне повышается и становится выше атмосферного на величину h1, указываемую манометром. Процесс 1-2 (см. рис. 1) осуществляется открыванием крана 3 с тем, чтобы давление в баллоне сравнялось с атмосферным. Затем идет процесс изохорического нагревания 2-3, в результате которого давление повышается и превышает атмосферное на величину h2.
Порядок выполнения работы
1. Открывают кран 3.
2. Насосом 2 нагнетают воздух в баллон и краном 3 отключают его от установки. (Во избежание выброса жидкости из манометра нужно делать 2-3 качания).
3. После того, как температура в баллоне станет равной температуре окружающей среды (давление в баллоне перестанет меняться); производят отсчет разности уровней жидкости в манометре h1 (снимают показания ма-
нометра в правом и левом коленах L1 и L2, берут их сумму или разность в зависимости от положения нуля отсчета).
4. Открыванием крана 3 дают воздуху, находящемуся в баллоне, достаточно быстро, а, следовательно, адиабатно расширяться до выравнивания давления в баллоне с атмосферным давлением. Кран 3 закрывают в момент, когда прекратится звук, возникающий при выходе воздуха, или же в момент, когда уровни жидкости в обоих коленах сравняются.
5. Как только газ, охлажденный при адиабатном расширении, нагреется до комнатной температуры (примерно через 2-3 минуты после закрытия крана 3), отсчитывают показания манометра L3 и L4 и находят h2.
6. Вычисляется значение по формуле (30).
7. Опыт повторяют не менее десяти раз при различных избыточных давлениях воздуха (значениях h1).
Обработка результатов измерений
1. Результаты проведенных измерений и вычислений записываются в таблицу.
Значения L1, L2, L3, L4, h1, h2 измеряются в миллиметрах столба жидкости, налитой в манометр.
| N | L1 | L2 | h1 = L1 ± L2 | L3 | L4 | h2 = L3 ± L4 |
| 
| 
| 
|
2. Вычисляется среднее значение .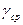
3. Рассчитываются абсолютные погрешности 
в каждом из опытов и
4. Записывается окончательный результат
5. Полученное значение сравнивается со значением 
, вычисленным теоретически, если считать воздух двухатомным газом.
Контрольные вопросы
1.Что называется теплоемкостью, удельной и молярной теплоемкостями? В каких единицах они измеряются?
2. Почему теплоемкости газов зависят от способов и условий их нагревания?
3. Как записывается первый закон термодинамики?
4. Что означают символы 
, 
, 
?
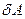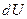5. Что называется внутренней энергией системы и по какому уравнению определяется изменение внутренней энергии идеального газа?
6. Как записывается первый закон термодинамики для различных изопроцессов идеального газа?
7. Почему Ср больше CV?
8. Какой процесс называется адиабатным? Выведите уравнение Пуассона.
9. Что происходит с внутренней энергией газа при адиабатном процессе?
10. Какие процессы используются в работе для расчета значения ?
11. Как рассчитать для воздуха теоретически?
