Точкові оцінки параметрів розподілу
Нехай об'єктом статистичного дослідження є деяка кількісна або якісна ознака (випадкова величина ξ), функція розподілу якої залежить від k невідомих параметрів α 1 α 2,..., α k (параметрів розподілу), тобто F(x) = F(x; α 1, α 2,..., α k)
Провівши при однакових умовах п незалежних експериментів, отримаємо вибірку з генеральної сукупності x1, x2,..., xn.
Означення 1. Точковою оцінкою параметра розподілу називається функція від значень хi (і =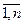 
), що спостерігались, яка (в певному розумінні) мало відрізняється від цього параметра.
За оцінку невідомого параметра розподілу можна запропонувати безліч різноманітних функцій вибірки, тому в математичній статистиці розглядаються оцінки, які задовольняють певним додатковим умовам, а саме: спроможності, незміщеності та ефективності.
Означення 2. Оцінка ã параметра а називається спроможною, якщо при n→∞ ã збігається за ймовірністю до α, тобто для будь-якого ε > 0
ε}=1.
Означення 3. Оцінка ã параметра а називається незміщеною, якщо для будь-якого натурального п математичне сподівання ã дорівнює а, тобто Мã(х1,х2,…,хп) = α.
Означення 4. Оцінка, яка має в певному класі оцінок мінімальну дисперсію називається ефективною.
Числові характеристики вибіркової сукупності.
Оцінки для математичного сподівання і дисперсії
Математичне сподівання і дисперсія є найбільш важливими числовими характеристиками випадкової величини. В класі лінійних функцій оцінкою для математичного сподівання є вибіркове середнє, яке обчислюється за формулами 
Ця оцінка є спроможною і незміщеною.
Розв'язання питання про те, чи можна вважати цю оцінку ефективною залежить від структури закону розподілу генеральної сукупності. Наприклад, для нормального закону розподілу ця оцінка ефективна.
Для дисперсії спроможною оцінкою є вибіркова дисперсія, яка обчислюється за формулами
Обчислення показують, що 
Отже,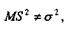 
тобто S2 є зміщеною оцінкою для ơ2.
Інтер оцінки.
Інтервальні оцінки параметрів розподілу
В багатьох випадках для невідомих параметрів потрібно знайти не точкову оцінку, а інтервальну, тобто побудувати інтервал, який з наперед заданою ймовірністю утримує невідоме значення параметра. Така задача була розв'язана при вивчені оцінки невідомої ймовірності через частоту.
Нехай fl(x1,x2,...,xn) і f2(xl,x2,...,xn) - деякі функції від вибіркових значень для яких завжди f1 ≤ f2; β- деяке дійсне число з інтервалу (0;1) (його називають надійним рівнем).
Означення 9. Якщо для параметра а теоретичного закону розподілу виконується співвідношення
Р { f1 ≤ α≤ f2 } ≥ β
То f1 i f2 називають надійними межами для цього параметра, а інтервал (f1; f2) - надійним (довірчим) інтервалом, що відповідають надійному рівню β.
ІV. Підсумок
V. Домашнє завдання
1. Прочитати конспект. Вивчити означення.
