Простейшая задача нахождения максимума функции решается по следующему алгоритму:
1. Задаются границы a и b, в пределах которых имеется максимум функции.
2. Интервал [a,b] разбивается на определенное количество шагов.
3. Функция табулируется в пределах заданного интервала, и каждое вычисленное значение функции сравнивается с максимальным (заданным до начала табулирования).
4. Находится максимальное значение функции на заданном интервале с определенным шагом и выводится на печать.
БЛОК-СХЕМА АЛГОРИТМА ИМЕЕТ ВИД:
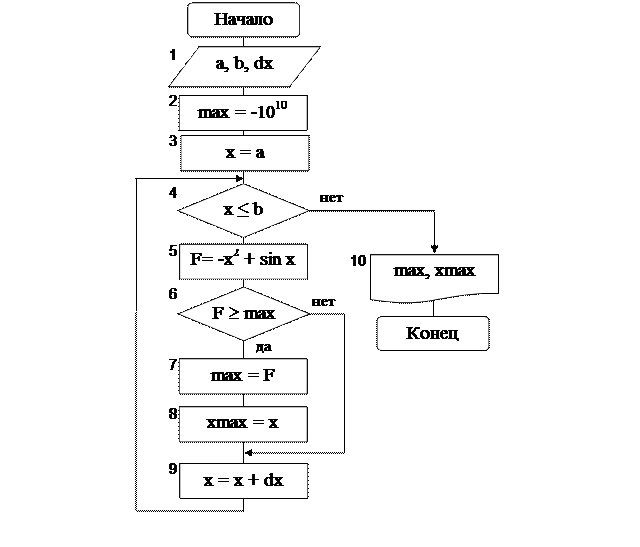
Рис. 4. Блок – схема алгоритма нахождения максимума функции
Естественно, что с уменьшением шага изменения аргумента точность вычисления максимума увеличивается.
Можно воспользоваться и следующим алгоритмом:
1. Найти значение максимума по алгоритму, представленному выше.
2. Для дальнейшего рассмотрения выбрать отрезок [xmax-dx, xmax+dx] и выполнить вычисление максимума с шагом, например, dx/10.
3. Сравнить два найденных значения.
max1 – значение максимума с шагом dx и max2 – значение максимума с шагом dx/10. Если |max2-max1| <=E (где Е – заданная степень точности вычисления), то закончить решение задачи и max2 вывести на печать, если нет, то вычисление продолжить дальше, повторяя п.2.
Такую задачу удобнее решать, используя процедуру нахождения максимального значения функции.
Блок – схема решения задачи имеет вид:
Рис. 5. Блок – схема алгоритма нахождения максимума функции
Методы оптимизации функций одной переменной
Метод равномерного поиска
Этот метод основан на том, что переменной x присваиваются значения x+∆x с шагом ∆x = const и вычисляются значения F(x). Если F(x n+1)>F(xn), переменной x даётся новое приращение. Как только F(xn+1)станет меньше F(x) поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.
Метод поразрядного приближения
Этот метод является разновидностью метода равномерного поиска и реализуется следующим алгоритмом:
1. Задаём начальное приближение x=x₀ слева от максимума F(x) и вычисляем F(x₀). Задаём D=h, где h=∆x – начальный шаг поиска.
2. Полагаем, что G=F(xn), где вначале F(xn)=F(x₀), задаём x=x+D и вычисляем F(x n+1)=F(x).
3. Проверяем условие F(x n₊₁)>G; если оно выполняется, идём к п.2, если нет, то к п.4.
4. Полагаем D=-D/4. Проверяем условие |D|>E/4, где E – заданная погрешность вычисления xn в точке максимума. Если оно выполняется, идём к п.2, т.е. обеспечиваем поиск максимума в другом направлении с шагом в 4 раза меньше прежнего. Если данное условие выполняется, процесс вычисления заканчиваем.
Метод дихотомии
Метод дихотомии (деление интервала поиска [a, b] пополам) реализуется следующим алгоритмом:
1. Проверяем условие |b-a|<2E, где E – заданная погрешность вычисления xn. Если это условие выполняется, идём к п.6; если не выполняется, идём к п.2.
2. Делим интервал поиска [a, b] пополам и вычисляем две абсциссы, симметрично расположенные относительно точки
x=(a + b)/2
x1=(a + b - E)/2 и x2=(a + b + E)/2
3. Для этих значений x вычисляем F(x₁)>F(x₂).
4. Проверяем условие F(x₁)>F(x₂). Если оно выполняется, полагаем b=x₂ и идём к п.1. Если не выполняется, идём к п.5.
5. Полагаем a=x₁ и идём к п.1.
6. Выводим на печать xn=(a+b)/2 и вычисляем F(xn).
Метод Фибоначчи
В методе Фибоначчи точка деления интервала исследования определяется с каждым новым расчётом (в методе дихотомии необходимо на каждом шаге выполнять два расчёта). В интервал исследования попадет предыдущий расчёт и для продолжения поиска достаточно произвести расчёт симметрично имеющемуся.
Допустим, задано число расчётов (шагов) N. Необходимо их произвести так, чтобы интервал, в котором лежит оптимум, был минимальным. Числа Фибоначчи, используемые в этом методе, определяются следующим образом:
FN=FN-1+FN-2
F0=F1=1
Алгоритм метода Фибоначчи состоит из следующих этапов:
1) Изменяют масштаб исходного интервала, в котором лежит оптимум. В качестве единицы измерения принимают 1=X₀/FN, или если задана длина l, в котором лежит оптимум, находят его на исходном интервале длиной X₀. Для этого, разделив X₀ на 1, находят ближайшее большее число Фибоначчи FN,
а по нему определяют N – число необходимых расчётов для определения интервала.
2) Расставляют первые две точки 
и 
на интервале исследования X0 на расстоянии FN-2 от конца b.
3) Вычисляют значение целевой функции в этих точках для сужения интервала исследования. Пусть 
> 
, тогда интервал [ , FN] исключается из рассмотрения.
4) На новом интервале исследования снова расставляют две точки 
и 
, но в одной из них уже известно значение целевой функции 
= .
5) Переходят к этапу 3 и т.д., пока не достигают искомого интервала, в котором находится значение переменной, максимизирующее её целевую функцию.
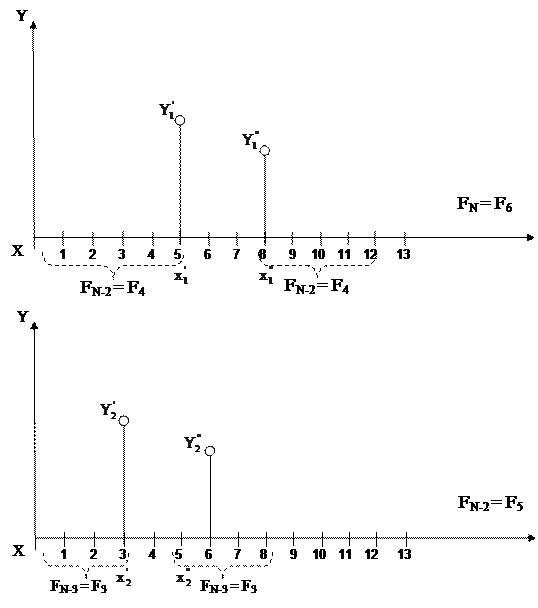На рис. 6 показан процесс сужения интервала исследования:
Рис. 6. Процесс сужения интервала исследования.
Последний N–й расчёт определяет интервал длиной l, в котором находится экстремум целевой функции.
Метод золотого сечения
Золотое сечение проводит деление отрезка АВ на две неравные части так, чтобы было справедливо соотношение (рис. 7).
Рис. 7
Метод золотого сечения позволяет сужать отрезок [a, b] каждый раз вычисляя лишь одно значение F(x), а не два, как в методе дихотомии.
Данный метод реализуется следующим алгоритмом:
1. Находим коэффициент дробления k=(√5-1)/2 отрезка [a, b].
2. Находим абсциссу х1=a + (1-k)*(b-a) и вычисляем F(x1).
3. Находим абсциссу х2=a + k*(b-a) и вычисляем F(х2).
4. Проверяем выполнение условия |x2-x1|<E, где E – заданная погрешность вычисления xn. Если это условие выполняется, вычисляем xn = (x1+ x2)/2 и F(xn), после чего останавливаем счёт с выдачей значений xm и F(xn). Если данное условие не выполняется, идём к п.5.
5. Проверяем условие F(x1) < F(x2). Если оно выполняется, полагаем, а = х1, х1 = х2 и F(x1) = F(x2), после чего идём к п.3. и п.4.
Если F(x1) ≥ F(x2), полагаем b = x2, x2 = x1, f(x1) = f(x2), после чего выполняем п.2 и п.4
