Инструкция пользователя компьютерной программой Texpasport

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Кафедра ТИ-1 «Технологическая информатика и технология машиностроения»

 

УТВЕРЖДАЮ

Заведующий кафедрой ТИ-1

_________________А.Ю.Албагачиев

«____»_________________2012 г.

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1

 

по дисциплине «УПРАВЛЕНИЕ ПРОЦЕССАМИ И СИСТЕМАМИ»

 

ТЕМА «Оценка технического совершенства и технического уровня режущего инструмента и определение необходимости его

постановки на производство»

 

 

Обсуждены на заседании кафедры

(предметно-методической секции)

«___»_________________20__г.

Протокол №__

 

 

Москва, 2012

 

Практическая работа №1

 

Сравнение режущих инструментов по их техническому совершенству и выбор наиболее эффективного с целью постановки его на производство

Цель работы: Обучение работе с паспортными данными продукции.

 

1. Порядок выполнения работы

 

Ознакомление с методом оценки технического совершенства продукции.

Ответы на контрольные вопросы (устно).

Определение исходных данных для сравнения вариантов продукции по её техническому совершенству.

Сравнительный анализ паспортных данных нескольких вариантов продукции и выбор наиболее эффективной.

Оформление отчета по практической работе.

 

 

2. Метод оценки технического совершенства продукции

 

2.1. Теоретические основы метода

На заключительном этапе стадии разработки продукции осуществляется ее передача на производство. Для осуществления передачи продукции от разработчика изготовителю, последнему нужна уверенность в том, что эта продукция будет пользоваться спросом.

Этой цели во времена существования у нас в стране системы государственных испытаний служил показатель технического уровня продукции. Очевидно, что сегодня он забыт незаслуженно. Однако, как само понятие, так и метод определения данного показателя требуют серьезной корректировки.

Технический уровень продукции – это относительная характеристика качества продукции, основанная на сопоставлении значений показателей, характеризующих техническое совершенство оцениваемой продукции с базовыми значениями соответствующих показателей.

Техническое совершенство некоторой продукции определяется, прежде всего, ее потребительскими свойствами. Т.е. оценка технического совершенства должна осуществляться по показателям, являющимся определяющими с точки зрения эффективности продукции на стадии ее эксплуатации. Такого рода показатель можно получить путем сопоставления с его помощью величины получаемого целевого параметра (целевой функции) с теми затратами, которые обеспечили получение данной величины целевого параметра (целевой функции) на стадии эксплуатации продукции.

Целевым параметром оцениваемой продукции является параметр, характеризующий выход процесса и отражающий удовлетворение конкретной потребности. Ради этого собственно и создается данная продукция.На входе процесса оцениваемая продукция может участвовать как объект или как средство.

Затратными являются все остальные параметры, характеризующие как вход, так и выход процесса, в котором участвует продукция с целью удовлетворения потребности.

В соответствии с вышеизложенным дадим определение понятию показателя технического совершенства продукции.

Показатель технического совершенства продукции – это показатель, определяемый совокупностью свойств, проявляющихся на стадии эксплуатации, и обуславливающих эффективность продукции в соответствии с ее назначением.

Тогда технический уровень продукции можно определять как частное от деления соответствующих показателей технического совершенства.

Оценку технического уровня следует производить на основании исходных данных, получаемых по строго определенным методикам в эталонных условиях, т.е. в лаборатории.

В качестве параметров для оценки технического совершенства продукции используются:

Т – наработка данной продукции до и между отказами или оперативное время, или технический ресурс;

Q – целевой параметр (целевая функция), получаемый за время Т;

q – расход данной продукции за время Т;

А – работа, совершенная с использованием данной продукции за

время Т.

Принятый набор параметров оценки не случаен. Он выбран таким образом, чтобы в нем были отражены все формы существования материального объекта: пространство, время и движение.

Значение показателя технического совершенства предлагается определять по областям возможного использования продукции.

Границы областей возможного использования продукции определяются в координатах, показанных на рис.1. Необходимо отметить

характерные для представленных квадрантов особенности.

Лучи, проведенные из начала координат в первом квадранте, являются линиями постоянных производительностей в единицу времени, т.е. .

Во втором квадранте лучи, проведенные из начала координат, являются линиями постоянных расходов продукции, т.е. q = const. В четвертом – линиями постоянной мощности, т.е. . В третьем квадранте – линиями постоянной эффективности продукции, т.е. .

 

Рис.1. Области возможного использования продукции

V, S, t и т.д. – параметры условий эксплуатации продукции, при которых получена точка М, расположенная на границе области ее возможного использования.

 

Определение границ областей возможного использования продукции осуществляется по результатам испытаний продукции в лабораторных условиях.

Критерием завершения испытания в отдельном опыте является предельное состояние продукции. Т.е., это такое состояние продукции, при

достижении которого дальнейшая ее эксплуатация невозможна.

Планирование экспериментов осуществляется таким образом, чтобы каждая их серия осуществлялась на отдельном луче производительности (см. рис.1, первый квадрант). Для каждого проведенного опыта фиксируются данные о том, при каких значениях параметров условий эксплуатации продукции – входных параметрах, например, для режущего инструмента: V – скорость, S – подача, t – глубина резанияи т.д., какие значения выходных параметров (T,Q,A,q и т.д.) получаются. Варьирование параметрами эксплуатации продукции осуществляется в широком диапазоне при всевозможных сочетаниях их значений, но при условии, что производительность остается постоянной ( = const). Серия экспериментов считается законченной лишь тогда, когда получено максимально возможное

значение целевого параметра Q и дальнейшее варьирование входными параметрами эксплуатации не приводит к его увеличению. Это значение параметра Q и соответствующее ему значение Т являются координатами экспериментальной точки, расположенной на границе области возможного использования продукции в первом квадранте.

Определение координат точек, расположенных на линии рационального использования продукции в первом квадранте, осуществляется следующим образом. Сначала значение Т, полученное на данном луче производительности, для экспериментальной точки, расположенной на границе области возможного использования, уменьшается на величину, гарантирующую не наступление предельного состояния продукции. Затем, исходя из величины производительности на данном луче, для уменьшенного значения Т вычисляется значение Q. Линии границ возможного использования определяются путём аппроксимации мод распределений значений, получаемых при повторной работе в условиях заключительных опытов каждой серии.

Количество серий экспериментов (количество лучей и конкретных значений производительностей) выбирается исходя из необходимого для построения (аппроксимации экспериментальных точек уравнением кривой) линии рационального использования продукции в первом квадранте. После определения уравнения, описывающего линию рационального использования продукции в первом квадранте, производится соответствующая корректировка значений Q и Т для граничных точек.

В четвертом квадранте построение линии рационального использования продукции осуществляется аналогичным образом. Разница заключается в том, что в данном квадранте в отличие от первого рассматриваются лучи постоянных мощностей. Причем максимальное значение работы – А, совершенной за соответствующее время наработки продукции до отказа – Т, получено при тех же условиях эксплуатации (V,S,t и т.д.), при которых за это время получено максимальное Q в первом квадранте.

Во втором квадранте построение линии рационального использования продукции осуществляется по следующим правилам. Для тех же условий эксплуатации (V,S,t и т.д.), которые определены для точек линии рационального использования в первом квадранте, берутся те же значения Q. Значение выходного параметра q, полученное при определении границ возможного использования продукции, с доведением ее до отказа, связанного с окончательным выходом продукции из строя, должно быть скорректировано. Коррекция осуществляется в сторону уменьшения расхода продукции за время – Т, исходя из того, что период наработки на отказ для точки, лежащей на линии рационального использования меньше, чем для точки, лежащей на границе области возможного использования продукции. Это априори гарантирует эксплуатацию продукции с отказами, приводящими лишь к нарушению ее работоспособного состояния, позволяющего ремонт и восстановление продукции.

В третьем квадранте построение линии рационального использования продукции осуществляется путем проецирования соответствующих точек из второго и четвертого квадрантов. Показатель технического совершенства продукции определяется по следующей формуле:

θR(θ)dθ,

где:

R = + A²; tgθ = .

 

Соответственно, показатель технического совершенства продукции будет тем лучше, чем будет больше его величина.

Показатель технического уровня определяется как частное от деления показателя технического совершенства опытной продукции на показатель технического совершенства продукции, принятой за базовую.

Опыт определения областей возможного использования продукции показал, что его применение требует существенных материальных затрат. Однако эти затраты единовременны и, следовательно, при дальнейшем применении данной продукции на производстве, могут потребоваться лишь выборочные испытания в конкретных точках. Номограммы же, с полученными линиями рационального использования, которые необходимо применять как паспортные данные на продукцию, будут пригодными для пользования на протяжении всего времени применения данной продукции. Это позволит потребителю использовать продукцию с наибольшим эффектом

.

2.2. Описание статистической обработки экспериментальных данных для построения областей возможного использования продукции и оценки её технического совершенства

 

Обработка результатов экспериментов, полученных по методике представленной в п. 2.1, осуществляется с использованием специального программного обеспечения.

Исходной информацией для работы программы служат данные о работе режущего инструмента в условиях заключительного опыта каждой серии и заносимые в форму, представленную в таблице 1.

 

Таблица 1

№ повторения заключительного опыта	T	Q	A	q
…	…	…	…	…

 

Таблица 1 состоит из пяти столбцов:

- в первом столбце записывается номер повторения опыта;

- второй столбец содержит время работы инструмента до или между

отказами (T);

- третий столбец содержит величины объёма припуска (Q), снятого за

время T;

- четвертый столбец содержит соответствующие величины работы (A),

произведённой за время T;

- пятый столбец содержит величины расхода инструмента (q) за

время T.

Для статистической обработки полученных данных повторений каждого заключительного опыта используем методы разработанные в [4].

Обработка данных осуществляется следующим образом:

1) находим среднее арифметическое результатов повторений заключительного опыта - ;

2) определяем дисперсию левую относительно среднего:

, для ;

3) определяем дисперсию правую относительно среднего:

, для ;

4) определяем величину, называемую мерой асимметрии:

.

Эта величина служит признаком типа распределения:

- при 1 > 0.359 - это экспоненциальное распределение;

- при = 1 - это нормальное распределение;

- при > 1 - это ассиметричное распределение.

Так как распределения характеристик режущего инструмента

практически в большинстве случаев не являются нормальными, в качестве основной зависимости будем рассматривать линию мод.

Значение моды (с), расчитывается по формуле:

где: - среднее всех результатов повторений;

а, σ – параметры получаем по таблицам, разработанным в [4].

Для оценки рисков при эксплуатации режущего инструмента необходимо иметь данные не только о моде распределения, но и о доверительном интервале его основных характеристик. Доверительным называют интервал, куда попадает искомая величина x с заданной вероятноcтью P, то есть:

P(B₁˂ x˂B₂)=1-α

где: α выбирают так, чтобы вероятность была равна P;

B₁, B₂ - границы интервала.

Для определения границ доверительного интервала здесь используются таблицы функции распределения, разработанной в [4]. По значениям меры асимметрии () и выбранной величине вероятности (P) в таблице функции распределения находим величину доверительного интервала.

В этом интервале с заданной вероятностью (P) гарантируется работа инструмента при выбранной производительности без поломок. Причём для эксплуатационников важна лишь нижняя граница доверительного интервала.

Поэтому для каждого заключительного опыта определялась точка, определяющая нижнюю границу доверительного интервала.

Аналогично поступаем со всеми повторениями всех заключительных опытов.

После статистической обработки исходных данных и получения значений мод (таблица 2) и нижней границы доверительного интервала (таблица 3) для каждого заключительного опыта сводим их в таблицы для расчета зависимостей и построения графиков.

Таблица 2

Заключительный опыт для заданной производительности	TС	QС	AС	qС
…	…	…	…	…

 

Таблица 3

Заключительный опыт для заданной производительности	TР	QР	AР	qР
…	…	…	…	…

 

Аппроксимируем полученные экспериментальные значения известными функциями.

Используем метод наименьших квадратов, суть которого состоит в том чтобы свести к минимуму сумму квадратов разностей между значениями искомой кривой и соответствующими значениями из таблицы

, (1)

где: - искомая аппроксимирующая функция;

- значения из таблицы 1.

Наиболее приемлемой для аппроксимации экспериментальных данных в 1-ом и 4-ом квадрантах. является показательная функция:

, (2)

где: е - это число е = 2.718281828 (экспонента).

В этой формуле нам неизвестны значения параметров а,b и с.

Будем определять эти параметры (а,b и с) используя формулу (1).

Для нахождения минимума функции U нужно взять производную от функции

(3)

и приравнять ее нулю.

Производную от функции (2) использовать нельзя, потому что производная от экспоненты равна самой себе, то есть , поэтому чтобы избавиться от экспоненты (е) нужно уравнение (2) прологарифмировать.

Из уравнения получаем:

(4)

Используя формулы (3) и (4) переписываем формулу (1) в виде:

(5)

Берем частные производные от функции по искомым величинам а,b и с и получаем систему из трех уравнений частных производных:

Видно, что эти уравнения обращаются в ноль при равенстве нулю выражения в скобках:

или

(6)

Получили уравнение достижения минимума расстояния между искомой функцией и величинами полученных экспериментальных значений. В левой части уравнения под величиной y_i при построении графика Q = f(T) следует понимать объём снятого припуска Q за время T, при построении

A = f(T) следует понимать работу A, совершённую за время T. Аргументом x в обоих случаях является время работы инструмента до

или между отказами (T)

Таким образом для всех опытов получаем систему уравнений:

…………………….

где: n – это число опытов для данного инструмента.

Для решения этой системы уравнений удобно представить ее в матричном виде:

, (7)

где:

Это вектор-столбец значений из таблицы входных данных. В нашем случае это значения столбцов производительности или работы из таблицы.

Это матрица содержит значения моментов времени отсчета из таблицы входных данных.

Это вектор-столбец искомых коэффициентов для функции (2) т.е.

Из матричного уравнения (7) по правилам аналитической геометрии следует что вектор-столбец искомых коэффициентов можно найти путем решения следующего матричного уравнения

где 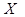- исходная матрица из таблицы входных данных

- транспонированная матрица получаемая их матрицы 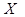путем

перемены местами строк и столбцов

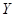- вектор-столбец, указанный выше

Выражение - это обратная матрица от произведения транспонированной и исходной матриц. Вычисляем обратную матрицу в этой работе методом из аналитической геометрии, где каждый элемент обратной матрицы получается путем вычисления алгебраического дополнения каждого элемента исходной матрицы и делением его на ранг исходной матрицы.

Подставив в вышеуказанные матрицы конкретные значения из исходной таблицы, и решая матричные уравнения получаем вектор содержащий три числа, которые и есть искомые коэффициенты для уравнения :

- первое число вектора – это откуда получаем коэффициент:

- второе число вектора – это коэффициент b

- третье число вектора – это коэффициент c

Подставляя найденные коэффициенты в уравнение (2) строим соответствующие графики.

Во втором квадранте строится зависимость Q = f(Q/q). Эту зависимость аппроксимируем формулой («Декартова листа»):

(8)

где: а – это коэффициент, который нужно определить используя столбец (q) из таблицы исходных данных.

y – это Q;

x – это Q / q.

Это неявное уравнение, то есть нельзя явно выразить одну переменную через другую.

Для построения этого графика нужно применять косвенные методы. В данном случае используем способ преобразования данного уравнения к неполному кубическому.

Для этого фиксируя произвольное значение на оси x и подставляя это значение в уравнение (8) получаем неполное кубическое уравнение.

Например, приняв х = 1, получаем:

(9)

Для решения этого уравнения используем метод вспомогательных величин.

Решая неполное кубическое уравнение для конкретного значения x получаем три корня: два положительных и один отрицательный. Так как отрицательные значения практического значения не имеют, поэтому отрицательные значения мы отбрасываем.

График «Декартова листа» имеет вид петли состоящий из двух ветвей (назовем их верхней и нижней). Эти ветви симметричны относительно оси графика.

Продолжая фиксировать значения по оси x и решая соответствующие неполные кубические уравнения получаем два массива соответственно для верхней и нижней ветвей графика. Движение по оси x прекращаем в тот момент, когда при решении неполного кубического уравнения вместо действительных положительных корней появляются мнимые корни. Это означает что верхняя и нижняя ветви практически сомкнулись.

Вследствие симметричности ветвей графика для нахождения коэффициента а дляформулы (9) используем также метод наименьших квадратов и аппроксимируем функцией .

Как и выше составляем уравнение:

и решая его соответствующим образом, находим коэффициент а.

Инструкция пользователя компьютерной программой Texpasport

“Определение технического совершенства инструмента”

Назначение программы

Компьютерная программа Texpasport предназначена для определения рациональных условий резания труднообрабатываемых материалов, используемых в авиадвигателестроении.

Программа выводит результаты своей работы в окне в виде графиков, отражающих области рационального использования инструмента.

В отдельном окне выводится величина, отражающая технический уровень изделия.

Программа предназначена для специалистов эксплуатирующих и изготавливающих режущий инструмент.

 

Установка и основные положения
эксплуатации программы «Texpasport»

 

Программа занимает на жестком диске компьютера1,74 MB дискового пространства. Для работы программы желательна следующая конфигурация компьютера:

— оперативная память не менее 512 МВ;

— тактовая частота процессора не менее 1,66 ГГц,

Для работы программы необходимо иметь операционную систему Microsoft Windows 2000 и выше;

Чем выше параметры памяти и частоты, тем быстрее производятся требуемые вычисления в программе. Оптимальная установка режима разрешения дисплея — 1024 х 768 точек

Установка программы не требует специальной компьютерной подготовки пользователя и производится копированием в выбранную им папку файла Texpasport.exe а также двух файлов с базами данных, описанных ниже.