Проранжируем исходный ряд статистических данных, т.е. расположим выборочные данные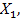 
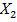
в порядке возрастания. В ранжированном вариационном ряду все элементы выборки упорядочены в виде неубывающей последовательности значений случайной величины Х.
Ранжированный ряд необходим для построения интервального вариационного ряда, поскольку объем выборки достаточно велик.(таблица 1.)
Интервал [4,03; 8,29] содержит все элементы заданной выборки. Разбиваем на частичные интервалы, используя при этом формулу Стерджеса для определения оптимальной длины и границ этих частичных интервалов. По формуле Стерджеса длина частичного интерваларавна:
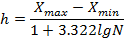
где,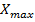 
и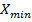 
- соответственно максимальное и минимальное значения выборки.
k =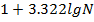 
– число интервалов, которое округляется до ближайшего целого числа.
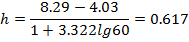
Округляем до h=0,6 и вычисляем последовательно границы частичных интервалов. За начало первого интервала принимаем значение:
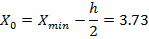
Далее вычисляем границы интервалов (начало второго интервала совпадает с концом первого и т.д.):
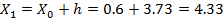
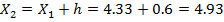
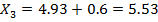
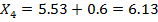
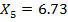
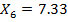
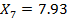
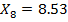
Заканчиваем вычисление границ, как только выполниться неравенство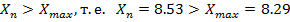 
Далее определяем частоты – количество ni элементов выборки, попавших в i-й энтервал (ni равно числу членов вариационного ряда, для которых справедливо неравенство xi-1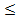 
xi* <xi, где xi-1, xi – границы i-го интервала; xi* - значения вариационного ряда).
По результатам вычислений составляем таблицу частот группированной выборки (таблица 2). В первой строке таблицы определим частичные интервалы, во второй строке – середины интервалов, в третьей строке запишем количество элементов выборки, попавших в каждый интервал – частоты; в четвертой – относительные частоты и в пятой – значения плотности относительных частот (значения выборочной, эксперементальной функции плотности)
Таблица 2.
Значения выборочной плотности распределения
| h | [3,73;4,33) | [4,33;4,93) | [4,93;5,53) | [5,53;6,13) | [6,13;6,73) | [6,73;7,33) | [7,33;7,93) | [7,93;8,53) |
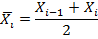
| 4.03 | 4.36 | 5.23 | 5.83 | 6.43 | 7.03 | 7.63 | 8.23 |
| ||||||||
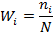
| 0.017 | 0.100 | 0.217 | 0.167 | 0.283 | 0.133 | 0.050 | 0.033 |
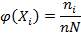
| 0.028 | 0.167 | 0.361 | 0.278 | 0.472 | 0.222 | 0.083 | 0.056 |
Посчитаем относительное количество наблюдений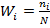 
попавших в данный интервал, а также плотность распределения относительных частот 
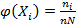, если длина h промежутков достаточно мала и объем выборки N велик (как в данном случае), то с вероятностью, близкой к единице, можно утверждать, что
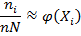
Иными словами функция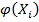 
является статистическим аналогом плотности распределения наблюдаемой в эксперименте случайной величины Х. плотность распределения относительных частот служит одной из основных характеристик интервального вариационного ряда.
Для наглядного представления о закономерностях изменения вариационного ряда построим график «гистограмма и полигон относительных частот». Для этого выбеем систему координат и по оси абсцисс отложим частичные интервалы [Xi-1, Xi) и середины этих интервалов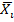 
, а по оси ординат – относительные частоты и плотность относительных частот.
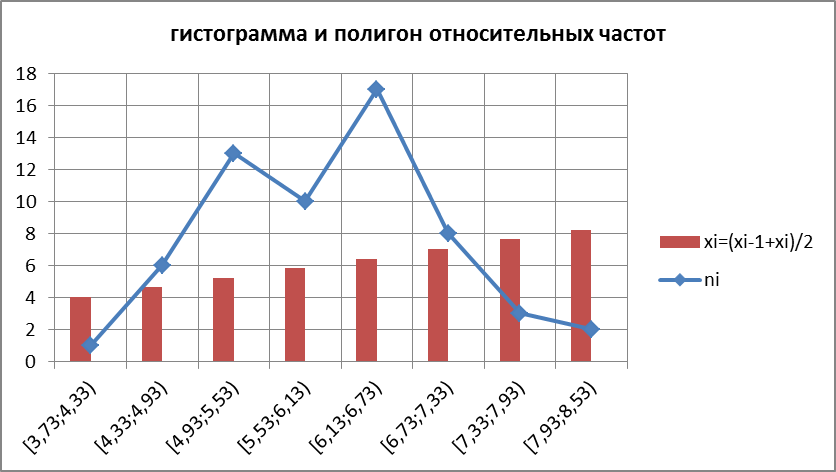
Анализируя вычисления в таблице 2, можно сделать вывод, что мода (наиболее часто встречающееся значение) экспериментального распределения имеет одно значение – локальный максимум в окрестности точки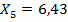 
с частотой n=17.
Используя вариационный ряд, находим оценку медианы (значение признака, который делит ряд пополам) по формуле:
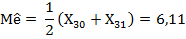
Сравним оценки медианы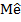 
и математического ожидания Х=6,35. Сравнение показывает, что они отличаются на 1,23%
