Метод неопределенных коэффициентов применяется для нахождения частного решения 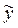 неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f (x), стоящая в правой части этого уравнения, имеет один из двух "специальных" видов:
неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f (x), стоящая в правой части этого уравнения, имеет один из двух "специальных" видов:
 , (42)
, (42)
где Pn (x) – многочлен степени n: Pn (x) = a 0 xn + a 1 xn– 1 +….+ an– 1 x+ an,
или
 , (43)
, (43)
где M и N – числа.
1) Если 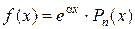 , то частное решение можно искать в виде:
, то частное решение можно искать в виде:
 (44)
(44)
где k 1, k 2 – корни характеристического уравнения, Qn (x) – многочлен степени n, записанный с неопределенными коэффициентами, подлежащими определению, например,
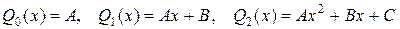 , и т. д.
, и т. д.
2) Если  , то частное решение
, то частное решение 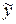 можноискать в виде:
можноискать в виде:
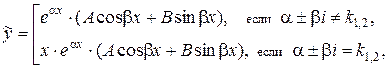 (45)
(45)
где k 1, k 2 – корни характеристического уравнения, А и В – неизвестные постоянные, подлежащие определению.
Пример 6. Найти общее решение уравнения  .
.
Решение.
1 этап. Построим общее решение y 0 соответствующего однородного уравнения 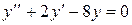 . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение  и найдем корни:
и найдем корни: 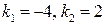 – корни вещественныеи различные. По табл. 4 определим вид линейно независимых частных решений однородного уравнения:
– корни вещественныеи различные. По табл. 4 определим вид линейно независимых частных решений однородного уравнения: 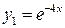 ,
, 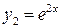 и запишем его общее решение:
и запишем его общее решение:
 .
.
2 этап. Построим частное решение данного неоднородного уравнения 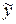 .В заданном уравнении
.В заданном уравнении 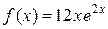 – правая часть 1-го специального вида:
– правая часть 1-го специального вида: 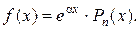 Здесь
Здесь  , Pn (x) = 12 x, т. е. многочлен в правой части – 1-й степени (n = 1). Число
, Pn (x) = 12 x, т. е. многочлен в правой части – 1-й степени (n = 1). Число  совпадает с одним корнем характеристического уравнения
совпадает с одним корнем характеристического уравнения  . Следовательно, согласно (44) частное решение
. Следовательно, согласно (44) частное решение 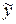 будем искать в виде:
будем искать в виде:
 ,
,
где А, B – неизвестные коэффициенты, подлежащие определению.
Найдем производные 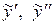 и подставим
и подставим 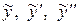 в данное неоднородное уравнение
в данное неоднородное уравнение  , при этом для простоты используем следующую форму записи:
, при этом для простоты используем следующую форму записи:

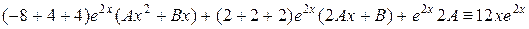 .
.
Здесь слева от черты записаны коэффициенты, с которыми 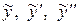 входят в уравнение, а под чертой приравниваются (тождественно) левая
входят в уравнение, а под чертой приравниваются (тождественно) левая
и правая части уравнения после подстановки в него 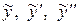 с группировкой подобных членов.
с группировкой подобных членов.
После сокращения обеих частей тождества на 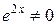 , получаем:
, получаем: 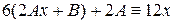 , откуда, приравнивая коэффициенты при х 1 и при х 0в обеих частях тождества, получаем:
, откуда, приравнивая коэффициенты при х 1 и при х 0в обеих частях тождества, получаем: 
Решая систему, находим  . Подставляя найденные значения в
. Подставляя найденные значения в 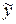 , получим:
, получим: 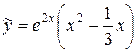 .
.
Объединяя результаты 2-х этапов, получаем общее решение
уравнения:
 .
.
Ответ: 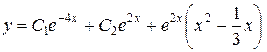 .
.
Пример использования метода неопределенных коэффициентов для случая, когда функция, стоящая в правой части уравнения, имеет 2-й специальный вид, приведен в образце выполнения контрольной работы.
6. Системы двух линейных дифференциальных уравнений
и их решение порядка методом повышения порядка
Нормальная система двух линейных дифференциальных уравнений
1-го порядка имеет вид:
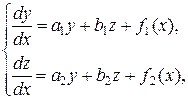 (46)
(46)
где х – независимая переменная, y (x) и z (x) – неизвестные функции, f 1(x)
и f 2(x) – известные функции a 1, a 2, b 1, b 2 – коэффициенты. Общее решение системы (46) имеет вид:
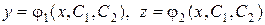 ,
,
где С 1 и С 2 – произвольные постоянные.
Для решения системы (46) методом повышения порядка необходимо исключить одну из неизвестных функций. Для этого можно выразить одну из функций, например, z (x), из одного уравнения системы:
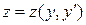 , (47)
, (47)
продифференцировать ее и подставить z и  во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида
во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида 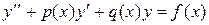 . После получения его решения
. После получения его решения  , следует, используя (47), найти вторую неизвестную функцию:
, следует, используя (47), найти вторую неизвестную функцию: 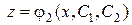 и записать ответ.
и записать ответ.
Если в системе (46) коэффициенты a 1, a 2, b 1, b 2 – постоянные, то в результате применения метода повышения порядка получается линейное неоднородное уравнение с постоянными коэффициентами:
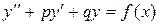 ,
,
решение которого рассмотрено в п. 5.
Пример использования метода повышения порядка для решения системы двух линейных дифференциальных уравнений 1-го порядка приведен в образце выполнения контрольной работы.
Примерный вариант и образец выполнения
контрольной работы 6
Задача 1. Дано дифференциальное уравнение 1-го порядка: 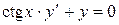 и точка
и точка  . Определить тип дифференциальногоуравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
. Определить тип дифференциальногоуравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
Задача 2. Дано дифференциальное уравнение 1-го порядка:  Определить тип дифференциального уравнения и найти егообщее решение.
Определить тип дифференциального уравнения и найти егообщее решение.
Задача 3. Дано дифференциальное уравнение 2-го порядка: 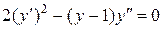 и начальные условия:
и начальные условия:  Определитьтип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Определитьтип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Задача 4. Дано дифференциальное уравнение 2-го порядка:  . Определить тип дифференциального уравнения
. Определить тип дифференциального уравнения
и найти его общее решение, используя метод вариации произвольных постоянных.
Задача 5. Дано дифференциальное уравнение 2-го порядка: 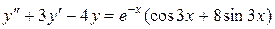 . Определить тип дифференциальногоуравнения и найти его общее решение, используя метод неопределенных коэффициентов.
. Определить тип дифференциальногоуравнения и найти его общее решение, используя метод неопределенных коэффициентов.
Задача 6. Дана система линейных дифференциальных уравнений 1-го порядка:  . Найти общее решение системы методом повышения порядка.
. Найти общее решение системы методом повышения порядка.
Решение задачи 1
Данное дифференциальное уравнение 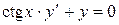 – уравнение
– уравнение
с разделяющимися переменными. Заменим 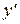 на
на  и разделим переменные, умножая обе части уравнения на
и разделим переменные, умножая обе части уравнения на 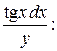
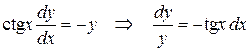 .
.
Интегрируя полученное равенство, получим:

откуда  . Заменяя
. Заменяя  , запишем общее решение данного уравнения:
, запишем общее решение данного уравнения: 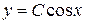 .
.
Найдем уравнение интегральной кривой, проходящей через точку  , т. е. частное решение, удовлетворяющее заданному начальному условию:
, т. е. частное решение, удовлетворяющее заданному начальному условию: 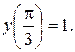 Для этого подставим в общее решение вместо x, y числа
Для этого подставим в общее решение вместо x, y числа 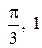 соответственно:
соответственно: 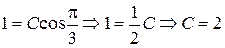 . Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М):
. Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М): 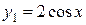 .
.
Найдем уравнения еще нескольких интегральных кривых.

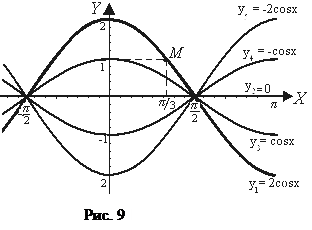 Построим все эти кривые
Построим все эти кривые
в системе координат (рис. 9).
Ответы: 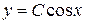 ;
;
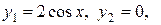
Интегральные кривые изображены на рис. 9.
Решение задачи 2
Данное дифференциальное уравнение  – это уравнение Бернулли (см. (27)), в котором
– это уравнение Бернулли (см. (27)), в котором 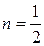 . Применим подстановку
. Применим подстановку 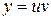 , тогда
, тогда 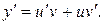 Подставив значения y и
Подставив значения y и 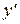 в уравнение, получим
в уравнение, получим 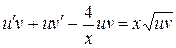 , или
, или
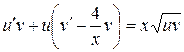 (****)
(****)
Найдем функцию v (x), решая уравнение 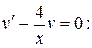
 .
.
Проинтегрируем левую и правую части этого уравнения:
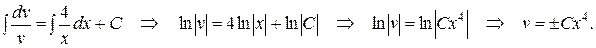
при соответствующем подборе 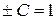 получаем
получаем 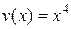 – частное решение уравнения
– частное решение уравнения 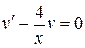 .
.
Подставляя найденную функцию 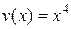
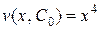 в (****), получим дифференциальное уравнение для функции u:
в (****), получим дифференциальное уравнение для функции u: 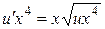 , или
, или  .
.
Найдем функцию 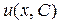 – общее решение этого уравнения:
– общее решение этого уравнения:
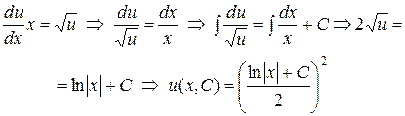
Общим решением исходного уравнения является функция
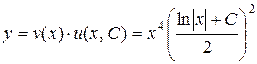 .
.
Ответ: 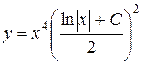 .
.
Решение задачи 3
Данное дифференциальное уравнение 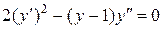 – это дифференциальные уравнения 2-го порядка,не содержащие независимой переменной x (см. (34)). Полагаем
– это дифференциальные уравнения 2-го порядка,не содержащие независимой переменной x (см. (34)). Полагаем 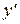 = p (y), тогда
= p (y), тогда  и уравнениепримет вид:
и уравнениепримет вид:
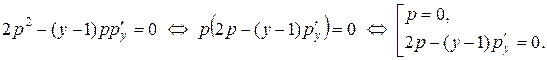
Решая первое уравнение, получим: 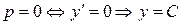 – первое семейство решений. Оно не удовлетворяет начальному условию
– первое семейство решений. Оно не удовлетворяет начальному условию 
Второе уравнение 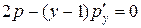 есть уравнение с разделяющимисяпеременными. Разделим переменные, заменяя
есть уравнение с разделяющимисяпеременными. Разделим переменные, заменяя  на
на  и проинтегрируем:
и проинтегрируем:
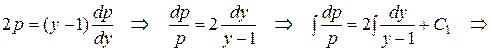
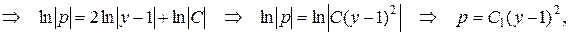
где 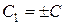 . Производя обратную замену p=
. Производя обратную замену p= 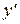 , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:
, получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:

Это уравнение с разделяющимися переменными. Прежде чем его интегрировать, целесообразно определить значение постоянной С 1, используя начальные условия (y = 3, 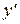 = 2 при х = 1):
= 2 при х = 1):
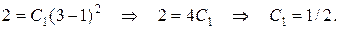
Подставив значение 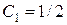 в дифференциальное уравнение, получим:
в дифференциальное уравнение, получим:
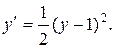
Разделяя переменные и интегрируя, найдем
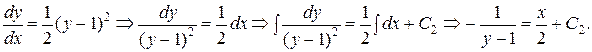
Здесь использовано: 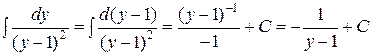 .
.
Определим значение постоянной С 2, соответствующее начальному условию y (1) = 3: 
Отсюда получим частный интеграл, удовлетворяющий заданным начальным условиям (решение задачи Коши): 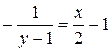 .
.
Получим частное решение уравнения, выразив y (x):
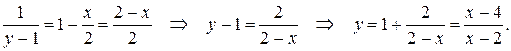
Ответ: 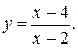
Решение задачи 4
Данное дифференциальное уравнение 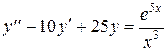 – это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид
– это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид  Найдем его в 2 этапа (см. п. 5.3.).
Найдем его в 2 этапа (см. п. 5.3.).
1 этап. Построим общее решение y 0 соответствующего однородного уравнения 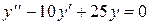 . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение 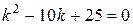 и найдем его корни:
и найдем его корни: 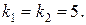 По табл. 4 определим вид его общего решения
По табл. 4 определим вид его общего решения 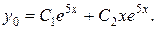
2 этап. Построим частное решение 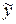 данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь
данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь 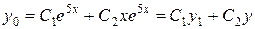 , т. е.
, т. е. 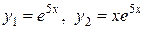 , тогда частное решение
, тогда частное решение 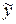 будем искать в виде
будем искать в виде 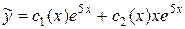 .
.
Составим условиям вариации согласно (40):

Поделив оба уравнения почленно на 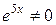 , получим систему с неизвестными
, получим систему с неизвестными  и
и 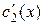 :
:
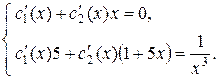
Для решения этой системы можно использовать метод исключения. Выразим  из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:
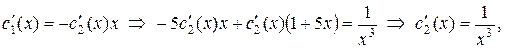
затем найдем 
Переходим к интегрированию:

(константы интегрирования считаем равными нулю).
Тогда 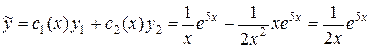 , и общее решение
, и общее решение
 .
.
Ответ: 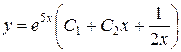 .
.
Решение задачи 5
Данное дифференциальное уравнение  –это линейное неоднородное дифференциальное уравнение 2-го порядка
–это линейное неоднородное дифференциальное уравнение 2-го порядка
с постоянными коэффициентами (см. (38)). Его общее решение имеет вид  Найдем его в 2 этапа.
Найдем его в 2 этапа.
1 этап. Построим общее решение y 0 соответствующего однородного уравнения  Составим для него характеристическое уравнение
Составим для него характеристическое уравнение 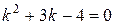 и найдем его корни:
и найдем его корни: 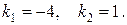 По табл. 4 определим вид его общего решения
По табл. 4 определим вид его общего решения 
2 этап. Построим частное решение 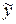 данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении
данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении 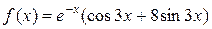 – правая часть 2-го специального вида:
– правая часть 2-го специального вида:  , где
, где  . Числа
. Числа 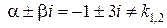 , тогда, согласно (45), частное решение
, тогда, согласно (45), частное решение 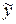 будем искать в виде:
будем искать в виде:

где А и В – неизвестные постоянные. Подставим 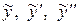 в данное неоднородное уравнение:
в данное неоднородное уравнение:
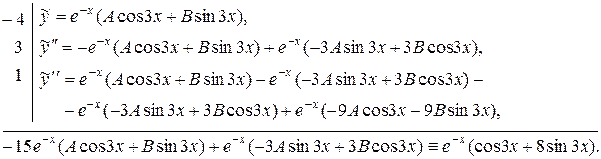
Сократим обе части тождества на  и приравняем коэффициенты при cos3 x и при sin3 x в левой и правой частях тождества.
и приравняем коэффициенты при cos3 x и при sin3 x в левой и правой частях тождества.

Решая полученную систему двух уравнений с двумя неизвестными, находим 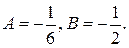 Подставив найденные значения А и В в выражение
Подставив найденные значения А и В в выражение 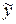 , получим частное решение неоднородного уравнения:
, получим частное решение неоднородного уравнения:
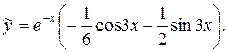
Объединяя результаты 2-х этапов, запишем ответ – общее решение данного уравнения.
Ответ: 
Решение задачи 6
Для решения системы  методом повышения порядка исключим из нее одну из функций – z (x).
методом повышения порядка исключим из нее одну из функций – z (x).
Выразим z (x) из первого уравнения системы: 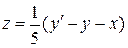 , продифференцируем ее:
, продифференцируем ее: 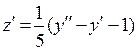 и подставим z и
и подставим z и 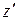 во второе уравнение системы:
во второе уравнение системы:
 .
.
После упрощения получаем дифференциальное уравнение 2-го порядка относительно функции у (х):
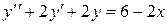 .
.
Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид 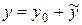 . Найдем его в 2 этапа.
. Найдем его в 2 этапа.
1 этап. Построим общее решение y 0 соответствующего одно-
родного уравнения 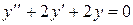 . Составим для него характе-
. Составим для него характе-
ристическое уравнение  и найдем корни:
и найдем корни: 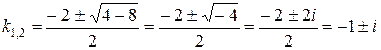 – корни комплексные сопряженные:
– корни комплексные сопряженные:  . Здесь
. Здесь 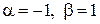 , тогда по таблице 4 определимвид общего решения однородного уравнения:
, тогда по таблице 4 определимвид общего решения однородного уравнения:
 .
.
2 этап. Построим частное решение 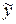 неоднородного уравнения. Здесь
неоднородного уравнения. Здесь 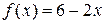 – правая часть 1-го специального вида:
– правая часть 1-го специального вида: 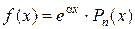 , где
, где 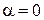 , n = 1. Число
, n = 1. Число 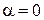 не совпадает с корнями характеристического уравнения
не совпадает с корнями характеристического уравнения 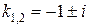 , тогда, согласно (44), частное решение
, тогда, согласно (44), частное решение 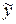 будем искать в виде:
будем искать в виде:
 ,
,
где А, B – неизвестные коэффициенты, подлежащие определению.
Найдем производные 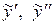 и подставим
и подставим 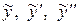 в неоднородное уравнение
в неоднородное уравнение  , при этом для простоты используем следующую форму записи:
, при этом для простоты используем следующую форму записи:

(здесь слева от черты записаны коэффициенты, с которыми 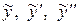 входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него
входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него 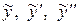 :
:
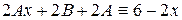 .
.
Приравнивая коэффициенты при х 1 и при х 0 в обеих частях тождества, получаем:
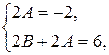
откуда находим: A = –1, B = 4. Подставляя найденные значения в 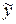 , получим:
, получим: 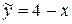 .
.
Объединяя результаты 2-х этапов, получаем общее решение уравнения 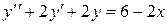 :
:
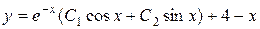 .
.
Найдем вторую неизвестную функцию:
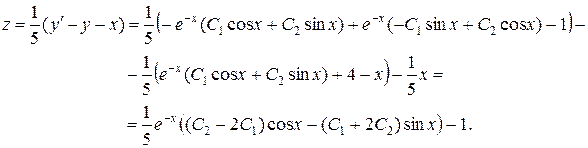
Ответ:

Варианты контрольнЫХ работ
Каждый вариант контрольной работы 5 для студентов-заочников
1 курса всех специальностей содержит 5 задач, охватывающих материал
по теме "Интегральное исчисление функции одной переменной". Каждый вариант контрольной работы 6 содержит 6 задач по теме "Дифференциальные уравнения".
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Интегрирование в контрольной работе 5 должно сопровождаться необходимыми ссылками на таблицы интегралов, их свойства, а также указанием метода интегрирования. При использовании замены переменной следует привести формулы замены всех элементов подинтегрального выражения через новую переменную.
Решение всех дифференциальных уравнений в контрольной работе 6 следует приводить подробно, указывая тип уравнения, способ получения решения и используемые методы интегрирования.
Варианты контрольной работы 5
Задача 1. Найти неопределенные интегралы:
| № варианта | Интегралы |
| n | 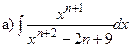 ; ; 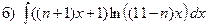 ; ;
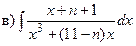 ; ; 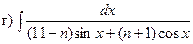
|
В примерах  правильность полученных результатов проверить дифференцированием.
правильность полученных результатов проверить дифференцированием.
Задача 2. Вычислить несобственные интегралы или доказать их расходимость:
| № варианта | Интегралы |
| n | а) 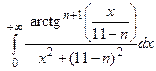 ; б) ; б) 
|
Задача 3. Вычислить с помощью определенного интеграла площадь плоской фигуры:
а) ограниченной в ДСК линиями l 1 и l 2;
б) ограниченной в ПСК линией l.
Сделать чертежи.
| № варианта | Уравнения линий | |
| а) | б) | |
| n | 
| 
|
Задача 4. Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями l 1и l 2. Сделать чертеж.
| № варианта | Уравнения линий |
| n |  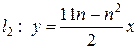
|
Задача 5. Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением y = f (x), где 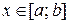 .
.
| № варианта | Уравнение кривой | Промежуток |
| n | 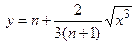
| 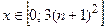
|
Варианты контрольной работы 6
Задача 1. Дано дифференциальное уравнение 1-го порядка и точка М. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
| № варианта | Дифференциальное уравнение | Точка |

| M (–2; 4) | |
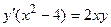
| M (0; 3) | |
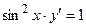
| M 
| |
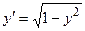
| M (0; 1) | |

| M (1; 2) | |

| M 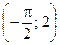
| |
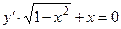
| M (0; –1) | |
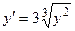
| M (0; 1) | |
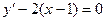
| M (2; 1) | |

| M (–1; 2) |
Задача 2. Дано дифференциальное уравнение 1-го порядка. Определить тип дифференциального уравнения и найти его общее решение.
| № варианта | Дифференциальное уравнение | № варианта | Дифференциальное уравнение |
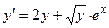
| 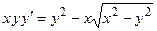
| ||
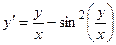
| 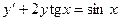
| ||
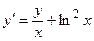
| 
| ||
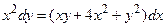
| 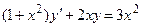
| ||
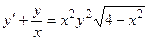
| 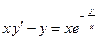
|
Задача 3. Дано дифференциальное уравнение 2-го порядка и начальные условия. Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
| № варианта | Дифференциальное уравнение | Начальные условия |
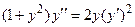
| 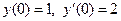
| |

| 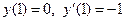
| |
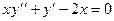
| 
| |
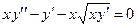
| 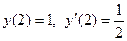
| |
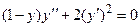
| 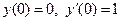
| |
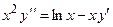
| 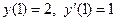
| |

| 
| |
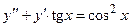
| 
| |
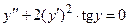
| 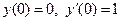
| |
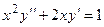
| 
|
Задача 4. Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
| № варианта | Дифференциальное уравнение | № варианта | Дифференциальное уравнение |
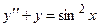
| 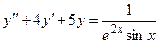
| ||
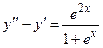
| 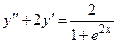
| ||
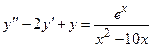
| 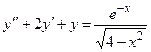
| ||
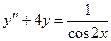
| 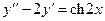
| ||
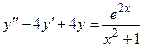
| 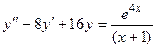
|
Задача 5. Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
| № варианта | Дифференциальное уравнение | № варианта | Дифференциальное уравнение |

| 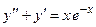
| ||

| 
| ||
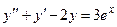
| 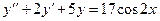
| ||

| 
| ||
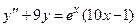
| 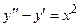
|
Задача 6. Дана система линейных дифференциальных уравнений 1-го порядка. Найти общее решение системы методом повышения порядка.
| № варианта | Система дифференциальных уравнений | № варианта | Система дифференциальных уравнений |

| 
| ||
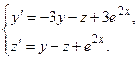
| 
| ||

| 
| ||
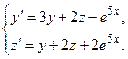
| 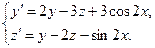
| ||
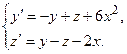
| 
|
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М.: Айрис-пресс, 2003. – 288 с.
2. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д.Т. Письменный. – М.: Рольф, 2002. – 256 с.
3. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев. – М.: Высш. шк., 1998. – 479 с.
4. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1999. – 304 с.
5. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1999. – 416 с.
6. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев. – М.: Высш. шк., 2001. – 304 с.
Налоговая льгота – Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3004 – воспитательная, образовательная и педагогическая литература
 |
Издательство МГТУ. 183010 Мурманск, Спортивная, 13.
Сдано в набор 06.04.2007. Подписано в печать 10.04.2007. Формат 60´841/16
Бум. типографская. Усл. печ. л. 3,02. Уч.-изд. л. 2,36. Заказ 194. Тираж 100 экз.






