Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b,
y = 0 и непрерывной кривой y = f (x), где 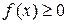 для
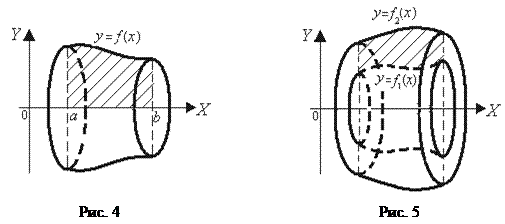
для  , вращается вокруг оси ОX. Объем полученного при этом тела вращения (рис. 4) вычисляется по формуле:
, вращается вокруг оси ОX. Объем полученного при этом тела вращения (рис. 4) вычисляется по формуле:
 . (14)
. (14)
Если плоская фигура ограничена линиями x = a, x= b, y 1 = f 1(x) и
y 2 = f 2(x), где 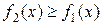 для
для  , то объем полученного при ее вращении вокруг ОX тела (рис. 5) можно вычислить по формуле:
, то объем полученного при ее вращении вокруг ОX тела (рис. 5) можно вычислить по формуле:
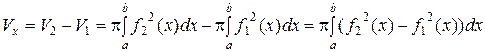 . (15)
. (15)
11. Вычисление длины дуги плоской кривой
Пусть плоская кривая АВ задана уравнением y = f (x), где  . Если функция f′ (x) и ее производная f′ (x) непрерывны на промежутке [ a; b ], то длина кривой АВ вычисляется по формуле:
. Если функция f′ (x) и ее производная f′ (x) непрерывны на промежутке [ a; b ], то длина кривой АВ вычисляется по формуле:
 . (16)
. (16)
Примерный вариант и образец выполнения
контрольной работы 5
Задача 1. Найти неопределенные интегралы:
 ,
, 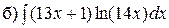 , в)
, в)  ,
,  .
.
В примерах  правильность полученных результатов проверить дифференцированием.
правильность полученных результатов проверить дифференцированием.
Задача 2. Вычислить несобственные интегралы или доказать их расходимость:
а)  , б)
, б)  .
.
Задача 3. Вычислить с помощью определенного интеграла площадь плоской фигуры:
а) ограниченной в ДСК линиями l 1:  и l 2:
и l 2:  ;
;
б ) ограниченной в ПСК линией l:  .
.
Сделать чертежи.
Задача 4. Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями
l 1: y = 2 x 2 и l 2: y = 6 x. Сделать чертеж.
Задача 5. Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением 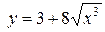 , где
, где  .
.
Решение задачи 1
а) Так как  , то используя формулу (3), получим:
, то используя формулу (3), получим:
 .
.
Проверим результат дифференцированием:

следовательно, выполнено условие (1).
Ответ:  =
=  .
.
б) Интеграл  относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим:
относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим:

 .
.
Проверим результат дифференцированием:


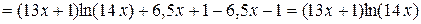 .
.
Ответ:  =
=  .
.
в) Подинтегральная функция является правильной рациональной дробью, поэтому ее можно представить в виде суммы простейших дробей:
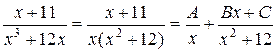 , отсюда
, отсюда
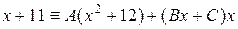 или
или  .
.
Неопределенные коэффициенты А, В, С найдем, приравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества:
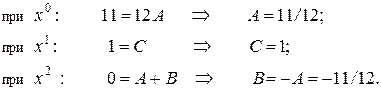
Коэффициенты А, В, С можно найти другим способом – подставляя
в тождество "удобные" значения х (метод частных значений):

Из первого уравнения получим: А = 11/12. Почленно вычитая два последних равенства, получим: 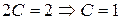 , и из последнего уравнения
, и из последнего уравнения
 .
.
Таким образом, 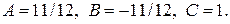
Переходим к интегрированию:

 .
.
Здесь использовано:
 ,
,
 .
.
Проверим результат дифференцированием:

 .
.
Ответ:  =
= 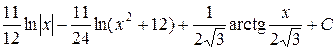 .
.
г) Применим универсальную тригонометрическую подстановку:


 .
.
Возвращаясь к переменной х, получаем:

Ответ:  =
=  .
.
Решение задачи 2
а) Данный интеграл является несобственным интегралом первого рода, поэтому
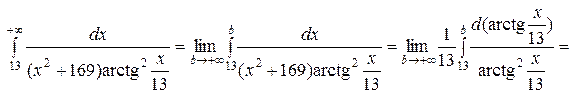

следовательно, интеграл сходится и равен  .
.
Здесь использовано:

Ответ: интеграл  сходится и равен
сходится и равен  .
.
б) Данный интеграл является несобственным интегралом второго рода, так как х = 13– точка бесконечного разрыва подинтегральной функции. Поэтому

 ,
,
следовательно, интеграл сходится и равен  .
.
Ответ: интеграл  сходится и равен
сходится и равен  .
.
Решение задачи 3
а) Найдем точки пересечения кривых, для чего составим и решим систему  . Приравнивая правые части, получаем уравнение
. Приравнивая правые части, получаем уравнение  , решив которое, найдем абсциссы точек пересечения: x = – 1, x = 3.
, решив которое, найдем абсциссы точек пересечения: x = – 1, x = 3.
Построим чертеж (рис. 6). На рисунке видно, что  на промежутке [ – 1; 3].
на промежутке [ – 1; 3].
 Используя формулу (12), вычислим площадь фигуры, ограниченной заданными линиями:
Используя формулу (12), вычислим площадь фигуры, ограниченной заданными линиями:


Ответ:  единиц площади.
единиц площади.
б) Для построения кривой  в ПСК составим таблицу значений функции на промежутке
в ПСК составим таблицу значений функции на промежутке  .
.

| π/4 | 2π/4 | 3π/4 | π | 5π/4 | 6π/4 | 7π/4 | 2π | |

| 12,7 | 11,3 | 11,3 | 12,7 |
 Построим чертеж в ПСК (рис. 7). Так как фигура ограничена кривой, заданной в полярной системе координат, то площадь фигуры, ограниченной заданной линией,вычислим по формуле (13):
Построим чертеж в ПСК (рис. 7). Так как фигура ограничена кривой, заданной в полярной системе координат, то площадь фигуры, ограниченной заданной линией,вычислим по формуле (13):
 .
.
Для  получаем:
получаем:
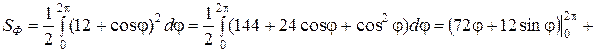
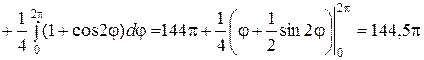 .
.
Ответ:  единицы площади.
единицы площади.
Решение задачи 4
Для построения фигуры Ф, ограниченной кривыми l 1 и l 2, нужно найти точки их пересечения, т. е. решить систему:  . Приравнивая правые части равенств, получаем уравнение 2 x 2 – 6 x = 0, решив которое, найдем абсциссы точек пересечения кривых: x = 0, x = 3.
. Приравнивая правые части равенств, получаем уравнение 2 x 2 – 6 x = 0, решив которое, найдем абсциссы точек пересечения кривых: x = 0, x = 3.
Объем тела вращения, полученного вращением фигуры Ф вокруг оси OX (рис. 8), можно найти как разность объемов двух тел по формуле (15):



 .
.
Ответ:  единиц объема.
единиц объема.
Решение задачи 5
Кривая задана уравнением 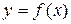 где
где  , поэтому ее длина вычисляется по формуле (16):
, поэтому ее длина вычисляется по формуле (16):  .
.
Для  получаем:
получаем:  , тогдадлина дуги кривой
, тогдадлина дуги кривой
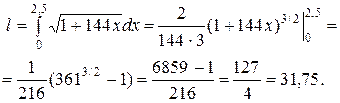
Ответ:  единиц длины.
единиц длины.
Справочный материал по теме
"Дифференциальные уравнения"






