Монотонность
Очень важным свойством функции является ее монотонность. Зная это свойство различных специальных функций, можно определить поведение различных физических, экономических, социальных и многих других процессов.
Выделяют следующие виды монотонности функций:
1) функция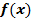 
возрастает, если на некотором интервале, если для любых двух точек 
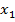и 
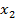этого интервала таких, что 
выполнено, что 
. Т.е. большему значению аргумента соответствует большее значение функции;
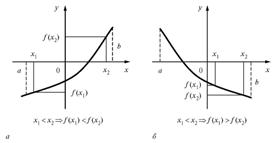
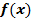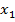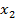2) функция убывает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что 
. Т.е. большему значению аргумента соответствует меньшее значение функции;
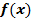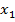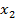3) функция неубывает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что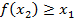 
;
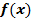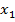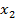4) функция невозрастает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что 
.
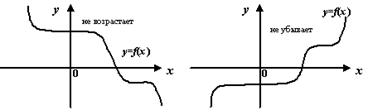
2. Для первых двух случаев еще применяют термин «строгая монотонность».
3. Два последних случая являются специфическими и задаются обычно в виде композиции из нескольких функций.
4. Отдельно отметим, что рассматривать возрастание и убывание графика функции следует именно слева-направо и никак иначе.
2. Четность/нечетность.
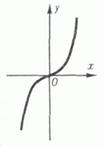
Функция называется нечетной, если при изменении знака аргумента, она меняет свое значение на противоположное. Формульная запись этого выглядит так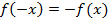 
. Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция изменит свой знак. График такой функции симметричен относительно начала координат.
Примерами нечетных функций являются 
и др.
Например, график 
действительно обладает симметричностью относительно начала координат:
Функция называется четной, если при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так 
. Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция в результате не изменится. График такой функции симметричен относительно оси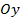 
.
Примерами четных функций являются 
и др.
К примеру, покажем симметричность графика 
относительно оси :
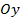Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида. У таких функций нет симметрии.
Такой функцией, например, является недавно рассмотренная нами линейная функция 
с графиком:
3. Особым свойством функций является периодичность.
Дело в том, что периодичными функциями, которые рассматриваются в стандартной школьной программе, являются только тригонометрические функции. Мы уже подробно о них говорили при изучении соответствующей темы.
Периодичная функция – это функция, которая не меняет свои значения при добавлении к аргументу определенного постоянного ненулевого числа.
Такое минимальное число называют периодом функции и обозначают буквой 
.
Формульная запись этого выглядит следующим образом: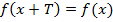 
.
Посмотрим на это свойство на примере графика синуса: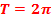 
Вспомним, что периодом функций 
и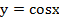 
является 
, а периодом 
и 
– 
.
Как мы уже знаем, для тригонометрических функций со сложным аргументом может быть нестандартный период. Речь идет о функциях вида:
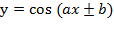
У них период равен 
. И о функциях:
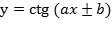
У них период равен 
.
Как видим, для вычисления нового периода стандартный период просто делится на множитель при аргументе. От остальных видоизменений функции он не зависит.
Ограниченность.
Функцию y=f(x) называют ограниченной снизу на множестве Х⊂D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.
Функцию y=f(x) называют ограниченной сверху на множестве Х⊂D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.
Если промежуток Х не указывается, то считают, что функция ограничена на всей области определения. Функция ограниченная и сверху, и снизу называется ограниченной.
Ограниченность функции легко читается по графику. Можно провести некоторую прямую у=а, и если функция выше этой прямой, то ограниченность снизу.
Если ниже, то соответственно сверху. Ниже представлен график ограниченной снизу функции. График ограниченной функции, ребята, попробуйте нарисовать сами.
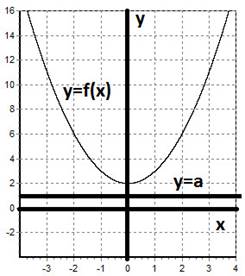
Пример:
Тема: Свойства функций: промежутки возрастания и убывания; наибольшее и наименьшее значения; точки экстремума (локального максимума и минимума), выпуклость функции.
Промежутки возрастания и убывания.
На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.
Вот формулировки признаков возрастания и убывания функции на интервале:
· если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
· если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
· найти область определения функции;
· найти производную функции;
· решить неравенства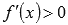 
и 
на области определения;
· к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма.
Пример:
Найти промежутки возрастания и убывания функции 
.
Решение.
На первом шаге нужно найти область определения функции. В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, 
.
Переходим к нахождению производной функции:
Для определения промежутков возрастания и убывания функции по достаточному признаку решаем неравенства 
и 
на области определения. Воспользуемся обобщением метода интервалов. Единственным действительным корнем числителя является x = 2, а знаменатель обращается в ноль при x=0. Эти точки разбивают область определения на интервалы, в которых производная функции сохраняет знак. Отметим эти точки на числовой прямой. Плюсами и минусами условно обозначим интервалы, на которых производная положительна или отрицательна. Стрелочки снизу схематично показывают возрастание или убывание функции на соответствующем интервале.
Таким образом, 
и 
.
В точке x=2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x=0 функция не определена, поэтому эту точку не включаем в искомые интервалы.
Приводим график функции для сопоставления с ним полученных результатов.
Ответ: функция возрастает при 
, убывает на интервале (0;2].
