А) аналитический (формула),
Б) графический (график),



 в) табличный х
в) табличный х
 у
у
3. Свойства функции:
· D(y) -область определения функции – это множество значений Х, где функция определена и выражена действительным числом.
· E(y) -область значений функции.
2. Периодичность, четность функции. Принести примеры.
а) Функция называется четной, если для любого Х из области
определения выполнено равенство:  .
.

 у
у
 Пример:
Пример: 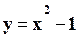 .
.
Проверим справедливость формулы:
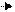

 х
х
График четной функции с имметричен относительно оси ОУ.
б) Функция называется нечетной, если для любого Х из области
определения выполнено равенство:  .
.


 Пример:
Пример:  . у
. у
Проверим справедливость формулы:




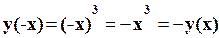
х
График нечетной функции
симметричен относительно начала координат.
в) Функция может быть ни четной ни нечетной.
3. Промежутки возрастания и убывания, максимумы и минимумы функций.
а) Функция называется возрастающей, если большему
значению Х соответствует большее значение функции:
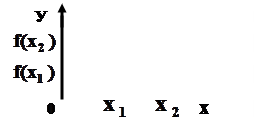 |





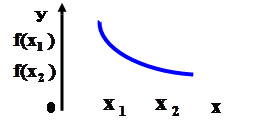
б) Функция называется убывающей, если большему
значению Х соответствует меньшее значение функции:
 |



 |
· Точки экстремума (точки максимума и минимума).

4. Преобразование графиков функций. Параллельный перенос.
 Для построения графика функции y=f(x)+b надо график функции y=f(x) перенести на b единиц вверх вдоль оси ОУ.
Для построения графика функции y=f(x)+b надо график функции y=f(x) перенести на b единиц вверх вдоль оси ОУ.
 Для построения графика функции y=f(x)-b надо график функции y=f(x) перенести на b единиц вниз вдоль оси ОУ.
Для построения графика функции y=f(x)-b надо график функции y=f(x) перенести на b единиц вниз вдоль оси ОУ.
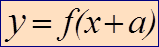 Для построения графика функции y=f(x+а) надо график функции y=f(x) перенести на а единиц влево вдоль оси ОХ.
Для построения графика функции y=f(x+а) надо график функции y=f(x) перенести на а единиц влево вдоль оси ОХ.
 Для построения графика функции y=f(x-а) надо график функции y=f(x) перенести на а единиц вправо вдоль оси ОХ.
Для построения графика функции y=f(x-а) надо график функции y=f(x) перенести на а единиц вправо вдоль оси ОХ.
5. Преобразование графиков функций. Деформация (растяжение и сжатие).
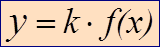 Для построения графика функции y=к·f(x) надо график функции y=f(x) растянуть в к раз вдоль оси ОУ.
Для построения графика функции y=к·f(x) надо график функции y=f(x) растянуть в к раз вдоль оси ОУ.
 Для построения графика функции y=1/к·f(x) надо график функции y=f(x) сжать в к раз вдоль оси ОУ.
Для построения графика функции y=1/к·f(x) надо график функции y=f(x) сжать в к раз вдоль оси ОУ.
 Для построения графика функции y=f(k·x) надо график функции y=f(x) сжать в к раз вдоль оси OX.
Для построения графика функции y=f(k·x) надо график функции y=f(x) сжать в к раз вдоль оси OX.
 Для построения графика функции y= f(1/к·x) надо график функции y=f(x) растянуть в к раз вдоль оси ОX.
Для построения графика функции y= f(1/к·x) надо график функции y=f(x) растянуть в к раз вдоль оси ОX.
6. Преобразование графиков функций. Отображение.
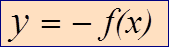 Для построения графика функции y= -f(x) надо график функции y=f(x) симметрично отобразить относительно оси OX.
Для построения графика функции y= -f(x) надо график функции y=f(x) симметрично отобразить относительно оси OX.
 Для построения графика функции y=f(-x) надо график функции y=f(x) симметрично отобразить относительно оси OУ.
Для построения графика функции y=f(-x) надо график функции y=f(x) симметрично отобразить относительно оси OУ.
7. Преобразование графиков функций: у = | f (х)| и у= f | (х)
| 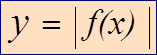 Построить график функции y=f(x), затем часть графика, расположенную над осью ОХ, оставить без изменения, а часть графика расположенную ниже оси ОХ симметрично отобразить вверх
Построить график функции y=f(x), затем часть графика, расположенную над осью ОХ, оставить без изменения, а часть графика расположенную ниже оси ОХ симметрично отобразить вверх
 Построить график функции y=f(x), затем часть графика, расположенную в области x<0, стереть и заменить симметричным отображением части графика из области x≥0 относительно оси OУ
Построить график функции y=f(x), затем часть графика, расположенную в области x<0, стереть и заменить симметричным отображением части графика из области x≥0 относительно оси OУ
8. Степень с произвольным действительным показателем и ее свойства.
Пусть дано положительное число 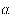 и произвольное действительное число
и произвольное действительное число  . Число
. Число  называется степенью, число
называется степенью, число 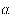 — основанием степени, число
— основанием степени, число  — показателем степени.
— показателем степени.
По определению полагают:
-
 .
. -
 .
. -
 ,
,  .
.
Если 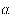 и
и  — положительные числа,
— положительные числа,  и
и  — любые действительные числа, то справедливы следующие свойства:
— любые действительные числа, то справедливы следующие свойства:
-
 .
. -
 .
. -
 .
. -
 .
. -
 .
. -
 .
.
9. Показательная функция, ее свойства и график для а >1
Функция вида  называется показательной.
называется показательной.
1.Область определения:D(у)= R,
2.Область значения: E(у)=(0;+  ),
),
3.При a>1 функция возрастает на всей числовой прямой,


 у
у

 1
1
Х
Возрастающая функция
а>1
10. Показательная функция, ее свойства и график для 0 < а<1.
Функция вида  называется показательной.
называется показательной.
1.Область определения:D(у)= R,
2.Область значения: E(у)=(0;+  ),
),
3. при 0<a<1 функция убывает на всей числовой прямой


 у
у
 |
Х
Убывающая функция
0<a<1
11. Степенная функция у=ха, её свойства и график для а >1
а- четное, ее свойства и график.
Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным показателем.
При n=2 получаем функцию y = х2, ее свойства:
Перечислим свойства функции у = х2.
1) Область определения функции — вся числовая прямая.
2) у = х2 — четная функция (f(— х) = (— x)2 = x2 = f (х)).
3) На промежутке [0; + οο) функция возрастает.
В самом деле, если  , то
, то  , а это и означает возрастание функции.
, а это и означает возрастание функции.
4) На промежутке (—оо; 0] функция убывает.
 В самом доле, если
В самом доле, если  ,то — х1 > — х2 > 0, а потому
,то — х1 > — х2 > 0, а потому
(—х1)2> (— х2)2, т. е.  , а это и означает убывание функции.
, а это и означает убывание функции.
Графиком функции y=х2 является парабола. Этот график изображен на рисунке.
Пусть n — произвольное четное натуральное число, большее двух:
n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |n| >1 тем круче идут вверх, чем больше n, а при  тем «теснее прижимаются» к оси х, чем больше n.
тем «теснее прижимаются» к оси х, чем больше n.
12. Степенная функция у=ха (0< а<1), ее свойства и график.
Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным показателем.
Рассмотрим функцию у = хr, где r — положительная несократимая дробь. Перечислим некоторые свойства этой функции.
1) Область определения — луч [0; + оо).
2) Функция ни четная, ни нечетная.
3) Функция у = хr возрастает на [0; +оо).

На рисунке II.5. изображен график функции  Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + оо).
Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + оо).
Подобный вид имеет график любой функции вида у = хr, где 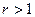 .
.
На том же рисунке изображен график функции  . Подобный вид имеет график любой степенной функции у = хr, где
. Подобный вид имеет график любой степенной функции у = хr, где  .
.
13. Степенная функция у=ха (а >1, а - нечетное), ее свойства и график).
Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным показателем.
При n = 3 получаем функцию у = х3, ее свойства:
1) Область определения функции — вся числовая прямая.
2)  y = х3 — нечетная функция (f (— х) = { — x)2 = — х3 = — f (x)).
y = х3 — нечетная функция (f (— х) = { — x)2 = — х3 = — f (x)).
3) Функция y = x3 возрастает на всей числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой.
График (кубическая парабола) изображен на рисунке
Пусть n — произвольное нечетное число, большее трех: n = = 5, 7, 9,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n. Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n.
14. Степенная функция, ее свойства и график для а<0.
Рассмотрим функцию у = х-n, где n — натуральное число. При n = 1 получаем у = х-n или у =  Свойства этой функции:
Свойства этой функции:
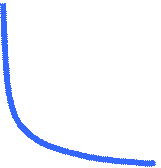
 График (гипербола) изображен на рисунке II.4.
График (гипербола) изображен на рисунке II.4.
Пусть n — нечетное число, большее единицы,
n = 3, 5, 7,.... В этом случае функция у = х-n обладает в основном теми же свойствами, что и функция у =  График функции у = х-n (n = 3, 5, 7,...) напоминает график функции у =
График функции у = х-n (n = 3, 5, 7,...) напоминает график функции у =  . Пусть n — четное число, например п = 2. Перечислим некоторые свойства функции у = х-2, т. е. функции y =
. Пусть n — четное число, например п = 2. Перечислим некоторые свойства функции у = х-2, т. е. функции y = 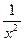 .
.
1) Функция определена при всех х  0.
0.
2) y = 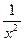 четная функция.
четная функция.
3) y = убывает на (0; +оо) и возрастает на (—оо;0).
Теми же свойствами обладают любые функции вида y = х-n при четном n, большем двух.
Рассмотрим функцию у = х-r, где r — положительная несократимая дробь. Перечислим свойства этой функции.
1) Область определения — промежуток (0; + оо).
2) Функция ни четная, ни нечетная.
3) Функция у = х-r убывает на (0; +оо).
15. Логарифмы, их свойства, основное логарифмическое тождество, формула перехода логарифма с одним основанием к логарифму с другим основанием.

Логарифмом положительного числа Х по основанию а называется показатель степени b, в которую нужно возвести основание а, чтобы получить число Х.
|
1. 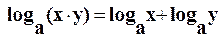 ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. 
16. Логарифмическая функция, у=1оqах, ее свойства и график для а > 1.
17. Логарифмическая функция, у=lодах, ее свойства и график для 0<а< 1.
Функция  называется логарифмической.
называется логарифмической.
1.Область определения: D(у)=(0;+  ),
),
2.Область значения: E(у)=R,
3.При a>1 функция возрастает на всей числовой прямой,
при 0<a<1 функция убывает на всей числовой прямой.

 у у
у у
 |
 | |||
 | |||
Х 0 1 х
Возрастающая функция Убывающая функция
а>1 0<a<1
18. Радианная и градусная мера угла, формула перехода от радианной меры к градусной и наоборот. Расположение углов по четвертям.
Определения.
Градусная мера угла – это величина угла в градусах.
Пример: прямой угол равен 90º.
Радианная мера угла – это величина угла в радианах.
Пример: прямой угол равен π/2 радиан.
Углом в 1 радиан называют центральный угол, длина дуги которого равна радиусу окружности (см.рисунок).

В тригонометрии обычно пользуются радианной мерой, так как она удобнее.
Соотношение градуса и радиана:
π
1º = —— рад
где π ≈ 3,14
180º
1 рад = ——
π
где π ≈ 3,14
Величина 1 радиана в градусах:
Угол в 1 радиан равен ≈ 57,3º:
180º 180º
1 рад = —— = —— ≈ 57,3º
π 3,14
Формулы для определения градусов и радиан:
π
xº = x · ——
где π ≈ 3,14
180º
x рад = x · ——
π
где π ≈ 3,14
Пример 1 (как выразить градусы в радианах):
π 30 π π
30º = 30 · —— = ———— = — рад.
180 180 6
π 2 π 2 · 3,14
72º = 72 · —— = —— = ———— ≈ 1,3 рад.
180 5 5
Пример 2 (как выразить радианы в градусах):
2π 2π 180º 2 · 180
—— рад = —— · ——— = ——— = 120º
3 3 π 3
180º 630º
4,5 рад = 3,5 · —— = ——— ≈ 200,5º
π 3,14

19. Определение тригонометрических функций.
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
К тригонометрическим функциям относятся следующие 4 функций: синус, косинус, тангенс, котангенс. Для каждой из указанных функций существует обратная тригонометрическая функция.
Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r = 1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.

Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sin α = y/r.
Поскольку r = 1, то синус равен ординате точки M(x,y).
Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cos α = x/r = x
Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tan α = y/x, x ≠ 0
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cot α = x/y, y ≠ 0
В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x, y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
20. Знаки тригонометрических функций.

21. Периодичность тригонометрических функций

Функцию у=f(x) называют периодической,если существует такое отличное от нуля число Т,что выполняется двойное равенство
f (x - T) = f(x) = f(x + T)
Т - период функции у=f(x)
sin (x - T) =sin x =sin (x + T). Аналогично для у=cos x
Функции у=sin x, у=cos x являются периодическими.Любое число вида 2k,где k =1,2,3,...,является периодом у=sin x, у=cos x.
Наименьший период функций у= tg x, y= ctg x является Любое число вида k,где k =1,2,3,....
22. Честность тригонометрических функций.
Функция y = f(x) называется четной, если для любого x из области определения функции выполняется равенство
f(-x) = f(x).
четные функции: y = /x/, y = x2, y = cos x
График четной функции симметричен относительно оси OY.
Функция y = f(x) называется нечетной, если для любого x из области определения функции выполняется равенство
f(-x) = - f(x).
нечетные функции: y = 1/x, y = x3, y = sin x, y = tg x, y = ctg x, y = arcsin x, y = arctg x
23. Соотношение между тригонометрическими функциями одного аргумента (с выводом).

24. Формула приведения (с примерами).
Это соотношения, с помощью которых значения тригонометрических функций аргументов  и др., выражаются через значения
и др., выражаются через значения  .
.
Правила преобразования:
1) Если аргумент содержит  , где n - нечетное натуральное число
, где n - нечетное натуральное число  , то функция меняется на "конфункцию", т.е. синус на косинус, тангенс на котангенс и наоборот. Если n - четное натуральное число
, то функция меняется на "конфункцию", т.е. синус на косинус, тангенс на котангенс и наоборот. Если n - четное натуральное число  , то название функции не изменяется.
, то название функции не изменяется.
2) Определяем знак ("+" или "- ") значения п ервоначальной функции. Преобразованное выражение сохраняет знак своего родителя
 .
.



25. Функция у= SinХ, ее свойства и график.
y = sin x, область определения: x ∈ ℜ, область значений: −1 ≤ sin x ≤ 1

26. Функция у= СоsХ, ее свойства и график.
y = cos x, область определения: x ∈ ℜ, область значений: −1 ≤ cos x ≤ 1

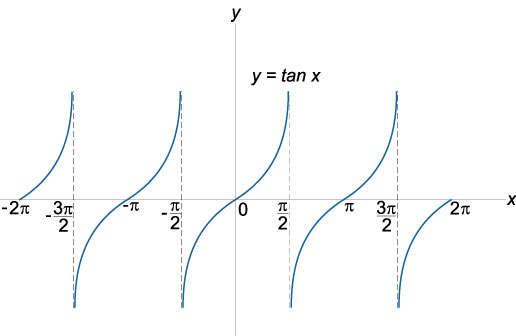
27. Функция у= tqХ, ее свойства и график
область определения: x ∈ ℜ, x ≠ (2k + 1)π/2 область значений: −∞ < tan x < ∞
28. Функция у= сtqX, ее свойства и график
y = cot x, область определения: x ∈ ℜ, x ≠ kπ, область значений: −∞ < cot x < ∞






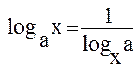 ;
7.
;
7.  ;
8.
;
8.  - основное
логарифмическое тождество.
- основное
логарифмическое тождество.

