НИЖНЕКАМСКИЙ ФИЛИАЛ
Экономический факультет
Кафедра «Высшей математики и информационных технологий»
МАТЕМАТИКА
КОНТРОЛЬНЫЕ РАБОТЫ
(I семестр)
Для направления обучения
«Менеджмент»
Нижнекамск - 2013
Оглавление
Аннотация. 5
Указания по выполнению контрольной работы.. 5
Контрольные задания. 6
Решение типовых примеров. 10
Аннотация
В данной работе рассматриваются основные способы и методы решения задач, необходимые для выполнения контрольного задания, приводится перечень теоретических вопросов.
Указания по выполнению контрольной работы
1. Номер варианта контрольной работы соответствует последней цифре номера зачетной книжки или студенческого билета.
2. В заголовке контрольной работы написать фамилию, имя, отчество, курс, группу, номер студенческого билета, вариант контрольной работы и дату сдачи ее в институт.
3. Решение задач располагать в порядке номеров, указанных в заданиях, сохраняя их номер. Перед решением каждой задачи выписать полностью условие. Решение каждой задачи сопровождать объяснениями и заканчивать ответом.
4. Оформление решений производить аккуратно, с минимальным количеством исправлений. Оставить поля для замечаний проверяющего.
Контрольные задания
1. Даны матрицы А, В, С. Вычислить матрицу D=AB+C
| Вариант | А | В | С |
| 1. |  
|  
| 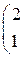 
|
| 2. |  
|  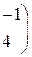
| 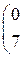 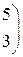
|
| 3. | 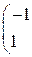 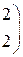
| 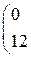 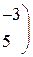
|   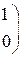
|
| 4. | 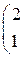 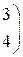
| 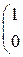 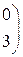
|  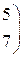
|
| 5. | 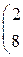 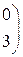
|  
| 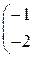 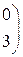
|
| 6. | 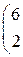 
|  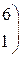
| 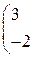 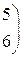
|
| 7. | 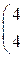 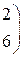
| 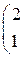 
|  
|
| 8. | 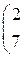 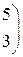
| 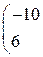 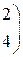
| 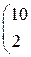 
|
| 9. |  
|  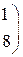
| 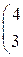 
|
| 10. | 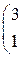 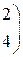
| 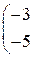 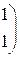
| 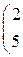 
|
Вычислить определитель третьего порядка
1. 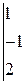 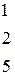 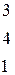 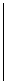
| 2. 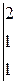 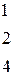 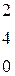 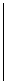
| 3. 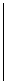 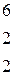  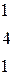 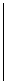
| 4. 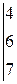 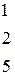 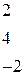 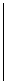
|
5. 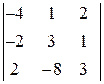
| 6. 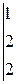 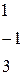 
| 7.  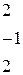 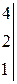
| 8. 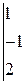 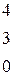 
|
9.   
| 10. 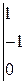 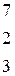 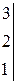 . .
|
Решить систему линейных уравнений
1. 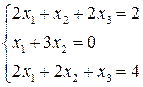 2.
2. 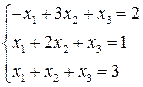 3.
3. 
4.  5.
5. 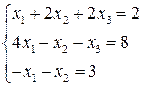 6.
6. 
7. 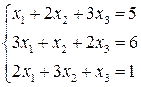 8.
8. 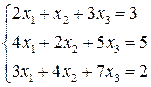 9.
9. 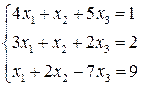
10. 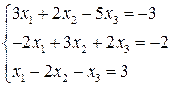
Составить уравнение прямой линии на плоскости, проходящей через заданные точки
1. (–1, 2) и (0, 10); 2. (–2, –1) и (3, 9); 3. (–3, 1) и (4, 8); 4. (–4, 3) и (–2, 7).
5. (–5, 2) и (0, 6); 6. (–6, –1) и (3, 5); 7. (–7, 1) и (4, 4); 8. (–8, 3) и (–2, 3).
9. (–9, 2) и (0, 2); 10. (–10, –1) и (3, 1).
5. Построить график функции (с помощью преобразования графиков основных элементарных функций) или в пакете MS Excel
1. 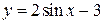 2.
2. 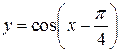 3.
3.  , 4.
, 4. 
5. 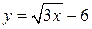 6.
6. 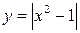 , 7.
, 7.  8.
8. 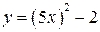 ,
,
9. 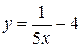 10.
10. 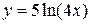
Значение функции f(x) известно в точках а и b. С помощью линейной интерполяции найти значение функции в точке с
| Вариант | а | f(a) | b | f(b) | c |
| -1 | 2,5 | ||||
| 1,5 | |||||
| 6,5 | 7,5 | 2,5 | |||
| 2,5 | 4,5 | 1,75 | |||
| –2 | –12,5 | –1 | –1 | ||
| 0,5 | |||||
| 1,5 | 3,5 | ||||
| 0,5 | 1,5 | 0,75 | |||
| 1,5 | 2,5 | ||||
| 0,5 | 1,4 |
Найти предел функции
1. 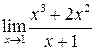 2.
2. 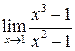 3.
3. 
4.  5.
5.  6.
6.  ,
,
7. 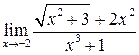 8.
8.  9.
9. 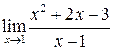 ,
,
10.  .
.
8. Вычислить производную функции
1. 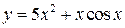 2.
2.  3.
3. 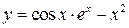
4. 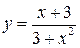 5.
5. 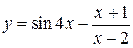 6.
6. 
7.  8.
8.  9.
9. 
10. 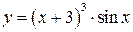
Найти наибольшее и наименьшее значения функции на отрезке [–2, 2].
1. f(x) = x3 – x2 – x + 1,
2. f(x) = x3 + 12x2 + 21x +10,
3. f(x) = x3 + 4x2 – 7,
4. f(x) = x3 – 6x +7,
5. f(x) = 4x3 – 8x2 – 3 x +10,
6. f(x) = x3 + 3x2 – 4,
7. f(x) = x3 – x2,
8. f(x) = x3 – 2x2 + x - 2,
9. f(x) = x3 – 2x2– x+2,
10. f(x) = x4 – 1.
10. Исследовать функцию и построить ее график. Проверить график в пакете MS Excel
1.  2.
2. 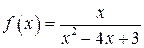 3.
3. 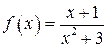 ,
,
4.  5.
5. 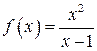 6.
6. 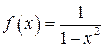 ,
,
7. 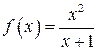 8.
8.  9.
9. 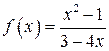 ,
,
10. 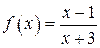 .
.
11. Вычислить приближенно, используя дифференциал функции
1. 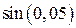 ; 2.
; 2.  ; 3.
; 3. 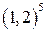 , 4.
, 4. 
5. 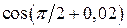 ; 6.
; 6. 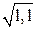 ; 7.
; 7. 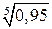 ; 8.
; 8. 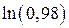
9. 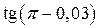 ; 10.
; 10.  .
.
Решение типовых примеров
1.1. Сложить две матрицы 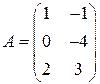 и
и 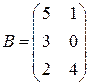
Решение. Складывать (вычитать) можно только матрицы одинакового размера, а т.к. размеры матрицы А – (3´2) и В – (3´2) (где 3 – число строк, 2 – число столбцов) совпадают, то для того, чтобы сложить две матрицы, надо к каждому элементу первой матрицы прибавить соответствующие элементы второй матрицы:
 +
+  =
= 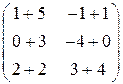 =
= 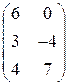 .
.
Ответ: 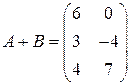 .
.
1.2. Умножить матрицу 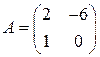 на число 3.
на число 3.
Решение. Для того, чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число:
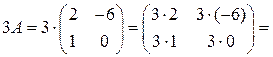
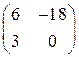 .
.
Ответ: 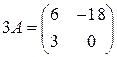 .
.
1.3. Умножить матрицу 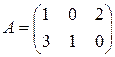 на матрицу
на матрицу  .
.
Решение. Умножение матриц А и В определено, если число столбцов первой матрицы равно числу строк второй.


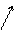 С m´n = A m ´ k ∙ B k ´ n
С m´n = A m ´ k ∙ B k ´ n
Совпадают
Размерность результирующей матрицы
В нашем случае размер А – (2´3), а размер В – (3´3), поэтому умножение производить можно; размерность результирующей матрицы С – (2´3). Для того чтобы получить элемент, стоящий на пересечении i –й строки и j –го столбца новой матрицы, нужно элементы i –й строки первой матрицы умножить на соответствующие элементы j –го столбца второй матрицы и результат сложить, т.е. элементы матрицы С вычисляются по формуле:
 .
.
C= 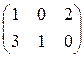 ∙
∙  =
= 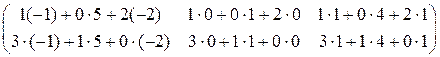
=  .
.
Ответ: C=  .
.
2. Вычислить определитель 3-го порядка: 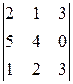 .
.
Решение. 1) Метод разложения по элементам строки или столбца.
С помощью метода разложения по элементам строки (столбца) можно вычислить определители любого порядка. Строку (столбец), по элементам которого производится разложение, следует выбирать так, чтобы в ней содержалось наибольшее количество нулей.
Разложим определитель по элементам какой-либо строки или столбца. Например, выберем для разложения третий столбец:
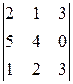 = 3∙ А13 + 0∙ А23 + 3∙ А33 = 3∙ А13 + 3∙ А33. (1)
= 3∙ А13 + 0∙ А23 + 3∙ А33 = 3∙ А13 + 3∙ А33. (1)
Здесь А13, А23, А33 – алгебраические дополнения элементов матрицы а13, а23, а33 соответственно, которые в общем случае для элемента аij находятся по формуле
Аij = (–1) i+j∙Mij. (2)
Минор Мij – определитель, получаемый из исходного вычеркиванием i ‑й строки и j ‑го столбца, на пересечении которых стоит данный элемент. Например, для нахождения М13 вычеркивается 1-я строка и 3-йстолбец:
 .
.
Аналогично определяем М23, вычеркивая 2-ю строку и 3-й столбец.
М33 получается вычеркиванием 3-й строки и 3-го столбца:
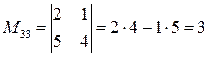 .
.
Тогда алгебраические дополнения (по формуле (2)) будут равны:
А13 = (–1)1+3 ∙M 13= (–1)4∙6 = 6,
А33 = (–1)3+3 ∙M 33=(–1)6∙3 = 3.
Подставляя найденные значения в (1), найдем определитель
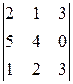 = 3∙6 + 3∙3 = 27.
= 3∙6 + 3∙3 = 27.
Ответ: 27.
2) Метод Саррюса.
С помощью метода Саррюса можно вычислять только определители третьего порядка.
Сначала к исходному определителю справа приписываем первый и второй столбцы:
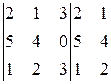
Тогда определитель равен сумме произведений элементов, стоящих на главной диагонали и диагоналях, параллельных ей, взятых со своими знаками, и произведению элементов побочной диагонали и параллельных ей диагоналях, взятых с противоположными знаками.

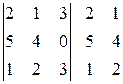 = 2∙4∙3 + 1∙0∙1 + 3∙5∙2 – 3∙4∙1 – 2∙0∙2 – 1∙5∙3 = 27.
= 2∙4∙3 + 1∙0∙1 + 3∙5∙2 – 3∙4∙1 – 2∙0∙2 – 1∙5∙3 = 27.
Ответ: 27.
3. Решить систему линейных уравнений:

1) Метод Крамера.
Выпишем определитель матрицы системы А:
Δ =  = 4.
= 4.
(Так как определитель не равен 0, то метод Крамера использовать можно, и система имеет единственное решение.)
Определитель Δ1 получаем из определителя Δ заменой первого столбца на столбец свободных членов В, а остальные столбцы остаются прежними:
Δ1 = 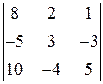 = 4.
= 4.
Аналогично, заменяя в исходном определителе второй, а затем третий столбцы на столбец свободных членов, получим соответственно Δ2 и Δ3.
Δ2 =  = 8, Δ3 =
= 8, Δ3 = 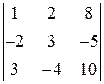 =12.
=12.
Теперь воспользуемся формулой Крамера и найдем все переменные:
 ,
, 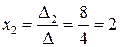 ,
,  .
.
2) Метод Гаусса.
Метод Гаусса – это универсальный метод решения систем линейных уравнений. Он заключается в последовательном исключении переменных.
Составим расширенную матрицу системы, которая включает в себя матрицу системы и столбец свободных членов.
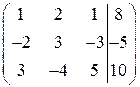 .
.
Произведем элементарные преобразования со строками матрицы, приведя ее к треугольному виду, т.е. к матрице, в которой все элементы, ниже главной диагонали равны нулю (при этом диагональные элементы не равны нулю).
Шаг 1. Если в матрице элемент а 11 = 0, то перестановкой строк нужно добиться того, чтобы элемент а 11≠ 0. В нашем примере а 11≠ 0.
Сначала обнулим элементы первого столбца ниже главной диагонали. Для этого поочередно умножим элементы первой строки на числа  и
и  , и прибавим соответственно к элементам второй и третьей строк:
, и прибавим соответственно к элементам второй и третьей строк:
2∙ -3
 +
+ 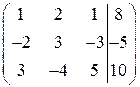 + →
+ → 
Шаг 2. Если в полученной матрице а 22 ≠ 0, то обнулим элемент второго столбца ниже главной диагонали. Для этого умножим вторую строку на число 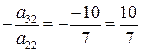 и прибавим к третьей строке:
и прибавим к третьей строке:
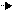

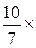
 →
→  .
.
Полученная матрица имеет треугольный вид.
Т.о. получили систему уравнений:

Откуда найдем из последнего уравнения х 3 = 3; из второго х 2 = 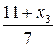 =2; из первого х 1 = 8 – 2 х 2 – х 3 = 1.
=2; из первого х 1 = 8 – 2 х 2 – х 3 = 1.
Ответ: х 1 = 1, х 2 = 2, х 3 = 3.
4. Составить уравнение прямой, проходящей через точки:
А (5; 4) и В (2; –3).
Решение. Уравнение прямой, проходящей через две точки М1(х1;y1) и М2(х2;y2) имеет вид: 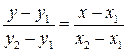 .
.
Уравнение прямой, проходящей через заданные точки:

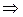

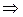
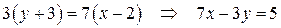 .
.
Ответ: уравнение прямой 
5. Построить график функции у = –4∙sin2 x + 1 (с помощью преобразования графиков основных элементарных функций).
 Решение.
Решение.
1) Сначала построим график функции у = sin x.
у



 1
1




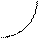
 О х
О х
 -π -
-π -  -1
-1  π
π
2) Сжатием графика в 2 раза вдоль оси Ох получаем график функции у =sin2 x.
 у
у



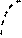
 1
1




 О х
О х
 -π -
-π - 
 π
π
3) Растянем график у = sin2 x вдоль оси Оу в 4 раза и получим график функции у = 4sin2 x.
у 


 4
4
 |


 1
1




 О х
О х
 -π -
-π - 
 π
π
 |


-4
4) Зеркально отобразив график относительно оси Ох, получим у = –4sin2 x.
у 


 4
4
 |


 1
1



 О х
О х
 -π -
-π - 
 π
π
 |


-4
5) Сдвинем полученный график на 1 единицу вверх параллельно оси Оу. Таким образом, график функции у = – 4∙sin2 x + 1 имеет вид:
у 


 5
5
 |







 1
1

 π
π  О
О  π х
π х
 |


-3
6. Значение функции известно в точках a и b. С помощью линейной интерполяции найти значение функции в точке с.
| а | f(a) | b | f(b) | c |
| 2,42 | 2,04 | 2,88 | 2,008 |
Решение. Формула линейного интерполирования:
f(c)» f(a) +  , где h = b – a, Df = f(b) – f(a).
, где h = b – a, Df = f(b) – f(a).
Подставляя в формулу известные значения из таблицы, получим:
f(2,008)» 2,42 +  = 2,512.
= 2,512.
Ответ. f(2,008)» 2,512.
7.1. Найти 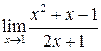 .
.
Решение. Так как под знаком предела стоит непрерывная в точке х =1 функция, то, используя определение непрерывной функции, имеем:
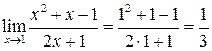 .
.
Ответ. 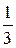 .
.
7.2. Найти 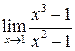 .
.
Решение. Функция 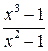 при х =1 не определена («неопределенность типа
при х =1 не определена («неопределенность типа 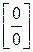 »), и, следовательно, не является непрерывной в этой точке. Но при всех других значениях х
»), и, следовательно, не является непрерывной в этой точке. Но при всех других значениях х
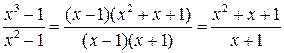 .
.
Полученная функция определена и непрерывна в точке х =1, поэтому
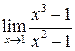 =
= 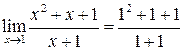 =
= 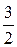 .
.
Ответ: 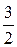 .
.
7.3. Найти 
Решение. Здесь требуется найти предел отношения двух бесконечно больших величин. О таком пределе заранее ничего определенного сказать нельзя («неопределенность типа  »). Преобразуем функцию под знаком предела, вынося за скобки х в старшей степени, и используем свойства бесконечно малых и бесконечно больших величин. Тогда имеем:
»). Преобразуем функцию под знаком предела, вынося за скобки х в старшей степени, и используем свойства бесконечно малых и бесконечно больших величин. Тогда имеем:

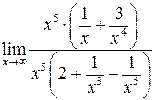 =
= 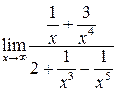 =
= 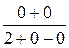 =
=  = 0.
= 0.
Ответ: 0.
8. Найти производную функции:
а) у = х + 2 б) y = (2 x – 3)(3 x + 2) в) у = 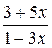
г) у = 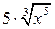 д) у = (x 3 – 2 x 2 + 5)6 е)
д) у = (x 3 – 2 x 2 + 5)6 е) 
ж) 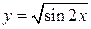 з) y = tg(3 x 2 – 1) и)
з) y = tg(3 x 2 – 1) и) 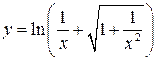 .
.
Справочный материал
Правила дифференцирования:
1) с’ = 0;
2) x’ = 1;
3) (u + v)’ = u’ + v’;
4) (c ∙ u)’ = c∙u’;
5) (u∙v)’ = u’ ∙ v + u ∙ v’;
6) (u∙v∙w)’ = u’∙v∙w + u∙v’∙w + u∙v∙w’;
7)  .
.
Производная сложной функции
Если у есть функция от и: у = f(u), где и в свою очередь есть функция от аргумента х: u = φ(x), т.е. если у зависит от х через промежуточный аргумент и, то у называется сложной функцией от х (функцией от функции): y = f(φ(x)).
Производная сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:
y’x = y’u u’x
Таблица производных:
| № | Функция у | Производная у’ |
| С | ||
| x | ||
| un | n∙un-1∙ u’ | |
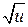
| 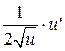
| |
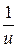
| 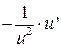
| |
| eu | eu∙u’ | |
| au | au ∙ln a ∙ u’ | |
| ln u | 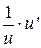
| |
| loga u | 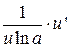
| |
| sin u | cos u∙u’ | |
| cos u | – sin u∙u’ | |
| tg u | 
| |
| ctg u | 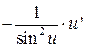
| |
| arcsin u | 
| |
| arcos u | – 
| |
| arctg u | 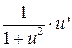
| |
| arcctg u | – 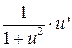
|
Решение. а) у = х + 2
Используя правило дифференцирования (3) и формулы (1), (2), имеем:
у' = (x + 2) ’ = (x) ’ + (2) ’ = 1 + 0 = 1.
б). y = (2 x – 3)(3 x + 2)
y’ = ((2 x – 3)(3 x + 2)) ’ = (2 x – 3) ’ ∙(3 x + 2) + (2 x – 3)∙(3 x + 2) ’ = 2∙(3 x + 2) + (2 x – 3)∙3 = 12 x – 5. Здесь мы использовали правило дифференцирования (5).
в) у = 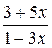
Используя правило дифференцирования (7), имеем
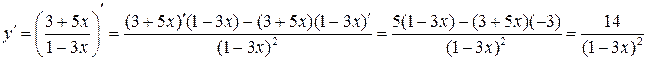
г) у = 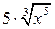
Найдем производную, используя правило дифференцирования (4) и формулу (3).
у' =  .
.
д) у = (x 3 – 2 x 2 + 5)6
Пусть x 3 – 2 x 2 + 5 = и, тогда у = и 6. По формуле (3), получим у’ = (и 6) ’ = 6 u 5∙ u’ = 6(x 3 – 2 x 2 + 5)5∙(x 3 – 2 x 2 + 5) ’ = 6(x 3 – 2 x 2 + 5)5∙(3 x 2 – 4 x).
е) 
По правилу дифференцирования (7) и формуле (10) получим:
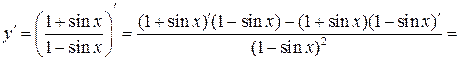
= 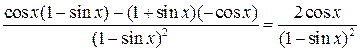 .
.
ж) 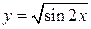
Используя формулы (4) и (10), имеем:
 .
.
з) y = tg(3 x 2 – 1).
По формуле (12) имеем:
y' = (tg(3 x 2 – 1)) ’ = 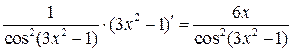 .
.
и) 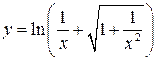 .
.
По формуле (8), а также (3), (4), (5) имеем:
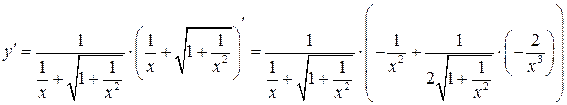 =
=
=  .
.
9. Найти наибольшее и наименьшее значения функции у = х 3 – 12 х на отрезке [0, 5].
Решение. Сначала найдем производную функции: у’ = 3 х 2 – 12.
Затем найдем критические точки, т.е. точки, в которых у’ = 0 или не существует: 3 х 2 – 12 = 0, откуда критические точки х 1 = –2, х 2 = 2. Точка х 1 = –2 не принадлежит отрезку [0, 5], поэтому мы исключаем ее из рассмотрения.
Вычислим значения функции в критической точке х 2 = 2 и на концах интервала и выберем из них наибольшее и наименьшее: у (2) = – 16, у (0) = 0, у (5) = 65.
Ответ: Наибольшее значение функции на отрезке [0, 5] равно 65, наименьшее значение равно –16.
10. Исследовать функцию у = 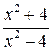 и построить ее график.
и построить ее график.
Решение. а) Найдем область определения функции.
Областью определения этой функции является вся действительная ось, за исключением двух точек х 1 = –2 и х 2 = 2, в которых имеет место разрыв (знаменатель х 2 – 4 = 0). Т.о. область определения: (-∞; -2)U(-2; 2)U(2; +∞)
б) Исследуем функцию на четность-нечетность.
Функция четная, т.к. у(-х) =  = у(х). Четность функции определяет симметрию ее графика относительно оси Оу.
= у(х). Четность функции определяет симметрию ее графика относительно оси Оу.
в) Найдем вертикальные асимптоты графика функции.
Вертикальные асимптоты следует искать в точках разрыва функции или на границе ее области определения. Точками разрыва являются х 1 = –2 и х 2 = 2.
Вычислим пределы функции в окрестностях этих точек.
Предел слева  , предел справа
, предел справа 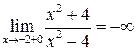 .
.
Аналогично 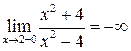 ,
, 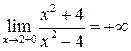 .
.
Следовательно, прямые х = –2 и х = 2 являются вертикальными асимптотами функции.
г) Найдем горизонтальные или наклонные асимптоты графика функции.
Для этого вычислим пределы: 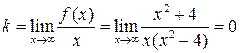 и
и 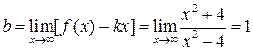 . Откуда (по формуле y = kx +b) заключаем, что уравнение горизонтальной асимптоты имеет вид: y = 0 x + 1, т.е. у = 1.
. Откуда (по формуле y = kx +b) заключаем, что уравнение горизонтальной асимптоты имеет вид: y = 0 x + 1, т.е. у = 1.
д) Найдем экстремумы и интервалы монотонности.
Производная заданной функции у’ = 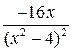 равна нулю (у’ = 0) при х= 0 и не существует при х = ±2. Но критической является только точка х= 0 (т.к. значения х = ±2 не входят в область определения функции). Поскольку при x < 0 f’(x) > 0, а при x > 0 f’(x) < 0, то х= 0 – точка максимума функции и f mах (x) =
равна нулю (у’ = 0) при х= 0 и не существует при х = ±2. Но критической является только точка х= 0 (т.к. значения х = ±2 не входят в область определения функции). Поскольку при x < 0 f’(x) > 0, а при x > 0 f’(x) < 0, то х= 0 – точка максимума функции и f mах (x) =  = – 1.
= – 1.

 На интервалах (–∞; –2) и (–2; 0) y' + –
На интервалах (–∞; –2) и (–2; 0) y' + –

 функция возрастает
функция возрастает  , на интервалах -2 0 2 x
, на интервалах -2 0 2 x
(0; 2) и (2; +∞) –. убывает y
е) Найдем интервалы выпуклости и точки перегиба.
Для этого надо найти вторую производную функции  . Видно, что уравнение
. Видно, что уравнение 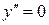 не имеет действительных корней, и это исключает существование у графика точек перегиба. Вместе с тем по корням знаменателя (–2 и 2) можно установить, что при переходе через эти значения х знаки
не имеет действительных корней, и это исключает существование у графика точек перегиба. Вместе с тем по корням знаменателя (–2 и 2) можно установить, что при переходе через эти значения х знаки  меняются.
меняются.
 На интервалах (–∞; –2) и (2; +∞) функция выпукла вниз, на интервале (–2; 2) – выпукла вверх.
На интервалах (–∞; –2) и (2; +∞) функция выпукла вниз, на интервале (–2; 2) – выпукла вверх.
ж) Найдем точки пересечения с осями координат.
f(0) =  = – 1, т.е. точка пересечения с осью ординат (0; -1). Уравнение f(х) = 0, (т.е.
= – 1, т.е. точка пересечения с осью ординат (0; -1). Уравнение f(х) = 0, (т.е. 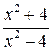 = 0), решений не имеет, следовательно, график функции не пересекает ось абсцисс.
= 0), решений не имеет, следовательно, график функции не пересекает ось абсцисс.
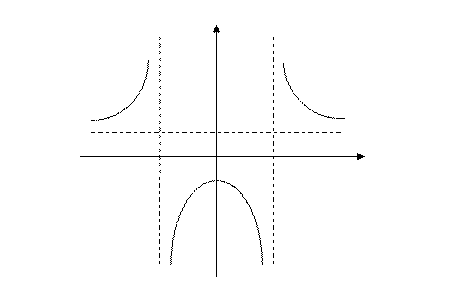 На основании полученных данных построим график заданной функции.
На основании полученных данных построим график заданной функции.
у
-2 2 х
-1
11. Вычислить приближенно, используя дифференциал функции 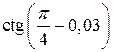 .
.
Решение. Для приближенных вычислений воспользуемся формулой:
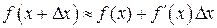 .
.
Положим  . Найдем производную
. Найдем производную 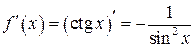 . Тогда
. Тогда 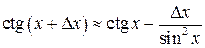 . Учитывая, что
. Учитывая, что  , возьмем
, возьмем  и
и 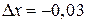 .
.
Тогда:

Ответ: