ѕервое начало термодинамики утверждает, что при превращении одной формы энергии в другую полна€ энерги€ системы не измен€етс€, однако не указывает никаких ограничений относительно возможности этого процесса. ѕоэтому первое начало термодинамики позвол€ет рассчитать энергетический эффект процесса, однако не дает ответа на вопросы о том, будет ли процесс протекать самопроизвольно, о направлении и глубине протекани€ процесса.
—амопроизвольный процесс Ц процесс, который может протекать без затраты работы извне, причем в результате может быть получена работа в количестве, пропорциональном произошедшему изменению состо€ни€ системы. —амопроизвольный процесс может протекать или обратимо, или необратимо. ’от€ определение обратимого процесса уже приводилось, следует подробнее рассмотреть это пон€тие. „тобы самопроизвольный процесс протекал обратимо, необходимо приложить извне такое сопротивление, чтобы переход был очень медленным и при бесконечно малом изменении противодействующей силы процесс мог пойти в обратном направлении. ¬ случае обратимо происход€щего изменени€ состо€ни€ системы производитс€ максимальное количество работы. ¬с€кий реальный процесс в какой-то степени €вл€етс€ необратимым, и получаема€ работа меньше максимально возможного теоретического количества.
¬ынужденный процесс Ц процесс, дл€ протекани€ которого требуетс€ затрата работы извне в количестве, пропорциональном производимому изменению состо€ни€ системы.
¬торое начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течени€ процесса. ƒалее, второе начало термодинамики дает возможность определить, какими должны быть услови€, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно дл€ решени€ различных задач прикладного характера. ѕодобно первому, второе начало термодинамики выведено непосредственно из опыта. ¬ то же врем€ второе начало термодинамики имеет ограниченную область применени€: оно применимо лишь к макроскопическим системам. ‘ормулировки второго начала термодинамики:
“еплота не может самопроизвольно переходить от менее нагретого тела к более нагретому.
Ќевозможен процесс, единственным результатом которого €вл€етс€ превращение теплоты в работу.
Ќевозможно построить машину, все действи€ которой сводились бы к производству работы за счет охлаждени€ теплового источника (вечный двигатель второго рода).
–ассмотрим работу тепловой машины, т.е. машины, производ€щей работу за счет теплоты, поглощаемой от какого-либо тела, называемого нагревателем. Ќагреватель с температурой “1 передает теплоту Q1 рабочему телу, например, идеальному газу, совершающему работу расширени€ ј; чтобы вернутьс€ в исходное состо€ние, рабочее тело должно передать телу, имеющему более низкую температуру “2 (холодильнику), некоторое количество теплоты Q2, причем
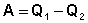 (I.34)
(I.34)
ќтношение работы ј, совершенной тепловой машиной, к количеству теплоты Q1, полученному от нагревател€, называетс€ термодинамическим коэффициентом полезного действи€ ( ѕƒ) машины η:
|
|
|
 (I.35)
(I.35)

–исунок 1.1. —хема тепловой машины
ƒл€ получени€ математического выражени€ второго начала термодинамики рассмотрим работу идеальной тепловой машины (машины, обратимо работающей без трени€ и потерь тепла; рабочее тело Ц идеальный газ). –абота машины основана на принципе обратимого циклического процесса Ц термодинамического цикла арно (рис. 1.2).

–исунок 1.2. ÷икл арно.
«апишем выражени€ дл€ работы на всех участках цикла:
”часток 1 Ц 2: »зотермическое расширение.
 (I.36)
(I.36)
”часток 2 Ц 3: јдиабатическое расширение.
 (I.37)
(I.37)
”часток 3 Ц 4: »зотермическое сжатие.
 (I.38)
(I.38)
”часток 4 Ц 1: јдиабатическое сжатие.
 (I.39)
(I.39)
ќбща€ работа в цикле равна сумме работ на всех участках:
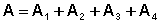 (I.40)
(I.40)
ѕровед€ р€д несложных преобразований, получим дл€ ѕƒ идеальной тепловой машины, работающей по циклу арно:
 (I.41)
(I.41)
“.о., максимальный ѕƒ тепловой машины не зависит от природы рабочего тела, а определ€етс€ только разностью температур нагревател€ и холодильника. ќчевидно, что без перепада температур превращение теплоты в работу невозможно. ѕолученное выражение справедливо дл€ тепловой машины, обратимо работающей по любому циклу, поскольку любой цикл можно разбить на множество бесконечно малых циклов арно.
ƒл€ необратимо работающей тепловой машины уравнение (I.41) преобразуетс€ в неравенство:
 (I.42)
(I.42)
ƒл€ общего случа€ можем записать:
 (I.43)
(I.43)
Ќа основе анализа работы идеальной тепловой машины арно можно сделать следующий вывод, €вл€ющийс€ также одной из формулировок второго начала термодинамики:
Ћюба€ форма энергии может полностью перейти в теплоту, но теплота преобразуетс€ в другие формы энергии лишь частично.
“.о., можно условно прин€ть, что внутренн€€ энергии системы состоит из двух составл€ющих: " свободной " X и " св€занной " Y энергий, причем "свободна€" энерги€ может быть переведена в работу, а "св€занна€" энерги€ может перейти только в теплоту.
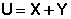 (I.44)
(I.44)
¬еличина св€занной энергии тем больше, чем меньше разность температур, и при T = const теплова€ машина не может производить работу. ћерой св€занной энергии €вл€етс€ нова€ термодинамическа€ функци€ состо€ни€, называема€ энтропией.
¬ведем определение энтропии, основыва€сь на цикле арно. ѕреобразуем выражение (I.41) к следующему виду:
 (I.45)
(I.45)
ќтсюда получаем, что дл€ обратимого цикла арно отношение количества теплоты к температуре, при которой теплота передана системе (т.н. приведенна€ теплота) есть величина посто€нна€:
 (I.46)
(I.46)  (I.47)
(I.47)
Ёто верно дл€ любого обратимого циклического процесса, т.к. его можно представить в виде суммы элементарных циклов арно, дл€ каждого из которых
 (I.48)
(I.48)
“.о., алгебраическа€ сумма приведЄнных теплот дл€ произвольного обратимого цикла равна нулю:
 (I.49)
(I.49)
¬ыражение (I.49) дл€ любого цикла может быть заменено интегралом по замкнутому контуру:
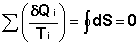 (I.50)
(I.50)
≈сли интеграл по замкнутому контуру равен нулю, то подынтегральное выражение есть полный дифференциал некоторой функции состо€ни€; эта функци€ состо€ни€ есть энтропи€ S:
 (I.51)
(I.51)
¬ыражение (I.51) €вл€етс€ определением новой функции состо€ни€ Ц энтропии и математической записью второго начала термодинамики дл€ обратимых процессов. ≈сли система обратимо переходит из состо€ни€ 1 в состо€ние 2, изменение энтропии будет равно:
|
|
|
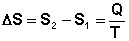 (I.52)
(I.52)
ѕодставл€€ (I.51, I.52) в выражени€ дл€ первого начала термодинамики (I.1, I.2) получим совместное аналитическое выражение двух начал термодинамики дл€ обратимых процессов:
 (I.53)
(I.53)
 (I.54)
(I.54)
ƒл€ необратимых процессов можно записать неравенства:
 (I.55)
(I.55)
 (I.56)
(I.56)
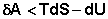 (I.57)
(I.57)
“.о., как следует из (I.57), работа обратимого процесса всегда больше, чем того же процесса, проводимого необратимо. ≈сли рассматривать изолированную систему (δQ = 0), то легко показать, что дл€ обратимого процесса dS = 0, а дл€ самопроизвольного необратимого процесса dS > 0.
¬ изолированных системах самопроизвольно могут протекать только процессы, сопровождающиес€ увеличением энтропии.
Ёнтропи€ изолированной системы не может самопроизвольно убывать.
Oба этих вывода также €вл€ютс€ формулировками второго начала термодинамики.






