Новая информация, которую необходимо усвоить при самостоятельной подготовке к практическому занятию.

Функциональная связь отражает строгую зависимость процессов или явлений. Изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину. Функциональная связь, как правило, проявляется при физических и химических явлениях, где её можно представить в виде уравнения, формулы. Примерами функциональной связи могут служить увеличение объема шара в строгой зависимости от увеличения его радиуса, расширение тела по мере увеличения температуры нагревания и т. д. При корреляционных связях, характерных для медико-биологических явлений, значению одного признака соответствуют разные значения других признаков. Корреляционная связь необходима, например, при оценке взаимосвязей между стажем работы и уровнем заболеваемости работающих; между разными уровнями физических факторов окружающей среды и состоянием здоровья; между различными уровнями интенсивности нагрузки и частотой (уровнем) физиологических реакций организма; между сроками госпитализации и частотой осложнений.

Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными).

2. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.

3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным признаком и множеством факторных признаков (при многофакторной связи).

Теснота связи количественно выражается величиной коэффициентов корреляции. Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определить «полезность» факторных признаков при построении уравнений множественной регрессии. Величина коэффициентов корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям.

Корреляционная связь бывает положительной – прямой (при увеличении одного признака увеличивается другой) и отрицательной – обратной (при увеличении одного показателя другой уменьшается). Коэффициент корреляции свидетельствует не только о направлении связи, но и об уровне этой связи. Сильная связь выражается коэффициентом от 0,7 до 0,99; средняя – от 0,3 до 0,69; слабая – до 0,29. При нулевом значении коэффициента связи отсутствуют.

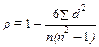Наиболее простым методом определения коэффициента корреляции является метод Спирмена – ранговая корреляция: ,где ρ – коэффициент ранговой корреляции; d – разность рангов; n – число сопоставляемых пар признаков. При ранговой корреляции числовые выражения сравниваемых статистических рядов ранжируют, то есть проставляют ранговые номера для каждой цифры (от 1 и далее) и подставляют значения в формулу с учетом разницы порядковых значений. Достоверность коэффициента определяют по таблицам критических значений, а также при расчете средней ошибки и критерия достоверности t.

Коэффициент ранговой корреляции используется в тех случаях, когда коррелируемые данные соответствуют количественному, качественному или порядковому распределениям, при этом является менее точным, чем коэффициент линейной корреляции.

Коэффициент линейной корреляции (метод Пирсона,метод квадратов) используется при количественном (числовом) выражении признака. При расчете коэффициента линейной корреляциисначала вычисляют среднее значение в каждом вариационном ряду сравниваемых групп. Затем находят отклонение каждой величины ряда от полученной средней. Для устранения отрицательных значений эти величины возводят в квадрат и подставляют в формулу: r_{xy =} ,где d_x и d_y – отклонение каждой варианты от своей средней арифметической М_х и М_{y .} По величине коэффициента устанавливают направление и силу связи. Достоверность коэффициента определяют по таблицам критических значений (таблицам Каминского) при n’ = n – 2, а также при расчете средней ошибки и критерия достоверности t. Коэффициент корреляции должен превышать свою ошибку не менее чем в 3 раза. 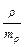Формула ошибки коэффициента ранговой корреляции: mр = , t = Ошибка коэффициента линейной корреляции вычисляется по формуле: m_{r =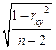} , t = . Значение t оценивается по таблице критических значений критерия Стьюдента t (при n < 30).

Регрессия (лат. regressio – обратное движение) в статистике –статистическая зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин, введена Фрэнсисом Гальтоном (1886).

В отличие от функциональной зависимости y = f (x), которая каждому значению независимой переменной x ставит в соответствие одно определённое значение величины y, при регрессионной зависимости одному и тому же значению x могут соответствовать различные значения величины y. Классическим примером средней регрессии служит зависимость среднего роста детей от роста родителей, а также зависимость среднего роста человека от его веса и т. п.

Регрессионный анализ – статистический метод, используемый для исследования отношений между двумя величинами. Регрессионный анализ используется для определения общего вида уравнения регрессии (наиболее часто используется линейная модель), оценки параметров этого уравнения, а также проверки различных статистических гипотез относительно регрессии.

Регрессионная модель основана на предположении о том, что величина x является контролируемой величиной, значения которой задаются во время эксперимента, а величина y – наблюдаемой в ходе эксперимента.

Корреляционно-регрессионный анализ является одним из методов статистического анализа взаимосвязи нескольких признаков.

Он определяется как метод, применяемый тогда, когда данные наблюдения можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону. Основная задача корреляционного анализа (основная и в регрессионном анализе) состоит в оценке уравнения регрессии.

Диаграмма рассеяния (поле корреляции). Поле корреляции – это графическое представление точек с координатами, определяемыми значениями двух переменных (независимой и зависимой) для всех наблюдений.

 

Вопросы по теме

1. Виды связей между явлениями. Теоретические основы вычисления и использования коэффициентов корреляции. Характеристика силы и направления связи при корреляционной зависимости.

2. Методика вычисления, область применения и оценка достоверно­сти коэффициента ранговой корреляции (метод Спирмена).

3. Методика вычисления, область применения и оценка достоверно­сти коэффициента линейной корреляции (метод Пирсона).

4. Коэффициент регрессии, область применения.

5. Выполнение самостоятельного задания (задачи 49–72) [1].

Рекомендательный библиографический список

Основной

1. Лисицын, Ю. П. Общественное здоровье и здравоохранение [Текст]: учебник / Ю. П. Лисицын, Н. В. Полунина. – М.: Медицина, 2002. – С. 153–157.

2. Лисицын, Ю. П. Общественное здоровье и здравоохранение [Текст]: учебник / Ю. П. Лисицын. – М.: Медицина, 2007. – С. 304–305, 308.

3. Захарова, Е. В. Сборник задач и самостоятельных работ [Текст] / Е. В. Захарова, И. Л. Сизикова. – Абакан: Издательство ФГБОУ ВПО «Хакасский государственный университет им. Н. Ф. Катанова», 2014. – С. 32–37.

4. Кучеренко, В. З. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения [Текст]: учебное пособие / В. З. Кучеренко. –
4-е изд., испр. и доп. – М.: ГЭОТАР-Медиа, 2007. – 192 с.

Дополнительный

1. Кича, Д. И. Руководство к занятиям по анализу и оценке общественного здоровья и здравоохранения (с применением медицинских информационных систем, компьютерных и телемедицинских технологий) [Текст]: учебное пособие / Д. И. Кича, В. И. Чернов, Н. Г. Куликова; под ред. академика РАМН, проф. И. Н. Денисова. – М., 2008. – 178 с. (электронная версия).

2. Медик, В. А. Руководство по статистике здоровья и здравоохранения [Текст]: руко­водство / В. А. Медик, М. С. Токмачев. – М.: ОАО «Издательство «Медицина», 2006. – 528 с.

3. Методические разработки семинарских занятий по курсу «Санитарная статистика» [Текст] / второй выпуск; под ред. П. А. Душенкова, Г. Н. Царик. – Кемерово, 2005. – 114 с.

4. Общественное здоровье и здравоохранение [Текст]: учебное пособие / под ред. Г. И. Куценко, А. И. Вялкова. – М: Медицина, 2003. – 495 с.

Электронные носители

1. Образовательный портал ХГУ им. Н. Ф. Катанова. – URL: http://edu.khsu.ru

2. ЭБС «Консультант студента» / Издательство ГЭОТАР-Медиа. – URL: http://studmedlib.ru/

Практическое занятие 6.
Метод стандартизации. Ошибки статистического анализа

Актуальность темы

Во многих медико-социальных, а также в клинических исследованиях, как правило, исключена возможность получения однородных групп для сравнения тех или иных показателей. Это касается в первую очередь показателей заболеваемости, общей смертности, рождаемости по городам, районам, странам, с разным составом населения по возрасту, полу и т. д. В таких случаях широкое применение находит метод стандартизации, позволяющий исключить влияние на общий показатель разного состава совокупностей по одному, двум или более признакам.

Цели занятия:

– познакомиться с методом стандартизации показателей, различными стандартными величинами;

– изучить различные способы стандартизации показателей;

– применить на практике полученные знания и выполнить самостоятельные индивидуальные задания.

Исходный уровень знаний и умений, необходимых для достижения поставленных целей: основы теории вероятности, математики, информатики, навыки работы с компьютером на уровне пользователя.