Отв. 
10,77; 
0,107; 
0,082;
772 Дж/(кг К); 
0,45 кг/м3
14. Генераторный газ состоит из следующих объемных частей: Н2 - 18%; СО = 24%; СО2 = 6%; N2 = 52%. Определить газовую постоянную генераторного газа и массовый состав входящих в смесь газов.
Отв. 342 Дж/(кг К); 10,86%;
60,03%; 1,48%; 
27,63%.
15. В цилиндр газового двигателя засасывается газовая смесь, состоящая из 20 массовых долей воздуха и одной доли коксового газа.
Найти плотность и удельный объем смеси при нормальных условиях, а также парциальное давление воздуха в смеси (данные о коксовом газе приведены в табл. IV, см. приложения).
Отв. 1,2 кг/м3; 
0,883 м3/кг;
0,884р
16. Определить газовую постоянную, плотность при нормальных условиях и объемный состав смеси, если ее массовый состав следующий: Н2 = 8,4%; СН4 = 48,7%; С2Н4=6,9%; СО=17%;СО2=7,6%; О2=4,7%; N2= 6,7%.
Отв. 
= 717 дж/(кг К); 
= 0,017;
= 0,028, 
=.0,484;
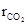= 0,02; 
= 0,518 Кг/м3.
17. Найти газовую постоянную, удельный объем газовой смеси и парциальные давления ее составляющих, если объемный состав смеси следующий: СО2 = 12%; СО = 1%; Н2О=6%; О2=7%; N2 = 74%, а общее давление её р = 100 кПа.
Отв. = 281 Дж/(кгК); 
= 0,76 м3/кг
= 1200 Па.
18. В резервуаре емкостью 125 м3 находится коксовый газ при давлении р = 0,5 МПа и температуре t = 18° С. Объемный состав газа следующий: =. 0,46; 
= 0,32; 
= 0,15; = 0,07. После из расходования некоторого количества газа давление его понизилось до 03 МПа, а температура — до 12° С.
Определить массу израсходованного коксового газа.
Отв. М 2167 кг.
19. Массовый состав смеси следующий: СО2 = 18%; О2 = 12% и N2=70.%. До какого давления нужно сжать эту смесь, находящуюся при нормальных условиях, чтобы при t = 180°С 8 кг её занимали объем, равный 4 м3.
Отв. р == 0,24 МПа.
20. Определить массовый состав газовой смеси, состоящей из углекислого газа и азота, если известно, что парциальное давление углекислого газа = 120 кПа, а давление смеси 
= 300 кПа.
Отв. 
=0,512; 
= 0,488.
21. Газовая смесь имеет следующий массовый состав: СО2 = 12%; О2 = 8% и N2= 80%.
До какого давления нужно сжать эту смесь, находящуюся при нормальных условиях, чтобы плотность её составляла 1,6 кг/м3?
Отв. До 0,213 МПа.
22. Пользуясь формулой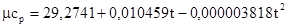 
, определить истинную мольную теплоемкость кислорода при постоянном давлении для температуры 700° С.
Сравнить полученное значение теплоёмкости со значением его, взятым из таблиц.
Отв. 
= 34,725 кДж/(кмоль К).
23. В регенеративном подогревателе газовой турбины воздух нагрёвается от150 до 600 °С.
Найти количество теплоты, сообщенное воздуху в единицу времени, если расход его составляет 360 кг/ч. Зависимость теплоёмкости от температуры принять нелинейной.
Отв. Q = 47,84 кДж/с.
24. При испытании двигателей внутреннего сгорания широким распространением пользуются так называемые гидротормоза. Работа, двигателя при торможении превращается в теплоту трения, и для уменьшения нагрева тормозного устройства применяют водяное охлаждение. Определить часовой расход воды на охлаждение тормоза, если мощность двигателя N = 33 кВт, начальная- температура воды 
= 15 °С, конечная 
= 60 ºС; принять, что вся теплота трения передается охлаждающей воде.
Отв. Мводы = 632 кг/ч.
25. При испытании нефтяного двигателя было найдено, что удельный расход топлива равен 231 г/(кВт ч).
Определить эффективный к. п. д. этого двигателя, если теплота сгорания топлива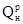 
=41 000 кДж/кг (9800 ккал/кг).
Отв. 
=0,38.
26. В котельной электростанции за 10 ч работы сожжено 100 т каменного угля с теплотой сгорания 29300 кДж/кг.
Найти количество выработанной электроэнергии и среднюю мощность станции, если к. п. д. процесса преобразования тепловой энергии в электрическую составляет 20%.
Отв. 162780 кВт ч,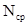 
=16278 кВт.
27. В сосуд, содержащий 5 л воды при температуре 20 °С, помещён электронагреватель мощностью 800 Вт.
Определить, сколько врёмени потребуется, чтобы вода нагревалась до температуры кипения 100°С. Потерями теплоты сосуда в окружающую среду пренебречь.
Отв. t = 30 мин.
28. В калориметр, содержащий 0,6 кг воды при t = 20 °С, опускают стальной образец массой 0,4 кг, нагретый до 200 °С. Найти теплоемкость стали, если повышение температуры воды составило 12,5 °С. Массой собственно калориметра пренебречь.
Отв. с =0,469 кдж/(кг К).
29. Свинцовый шар падает с высоты 100 м на твердую поверхность. В результате падения кинетическая энергия шара полностью превращается в теплоту. Одна треть образовавшейся теплоты передается окружающёй среде, а две трети расходуются на нагревание шара. Теплоёмкость свинца с = 0,126 кДж/(кг К). Определить повышение температуры шара.
Отв. Δt = 5,2 ºС
30. Автомобиль массой 1,5 т останавливается под действием тормозов при скорости 40 км/ч.
Вычислить конечную температуру тормозов t2, если их масса равна 15 кг, начальная температура t1 = 10 °С, а теплоемкость стали, из которой изготовлены тормозные части, равна 0,46 кДж/(кг К). Потерями теплоты в окружающую среду пренебречь.
Отв. t2 = 23,4 ºС
31. В газоходе смешиваются три газовых потока, имеющих одинаковое давление, равное 0,2 МПа. Первый поток представляет собой азот с объемным расходом V1 = 8200 м3/ч при температуре 200 °С, второй поток — двуокись углерода с расходом 7600 м3/ч при температуре 500 °С и третий поток воздуха с расходом 6400 м3/ч при температуре 800 °С.
Найти температуру газов после смешения и их объемный расход в общем газопроводе.
Отв t1 = 423 °С; V = 23000 м3/ч.
32. Продукты сгорания из газохода парового котла в количестве 400 кг/ч при темпёратуре 900 °С должны быть охлаждены до 500 °С и направлены в сушильную установку; Газы охлаждаются смешением газового потока с потоком воздуха при температуре 20 °С. Давление в обоих газовых потоках одинаковое.
Определить часовой расход воздуха, если известно, что Rгаз = Rвозд. Теплоемкость продуктов сгорания принять равной теплоемкости воздуха.
Отв. Мвозд = 366 кг/ч.
33. Газ при давлении р1 = 1 МПа и температуре = 200 ºС нагревается при постоянном объеме до t2 = 300 ºС. Найти конечное давление газа.
Отв. р2 = 1,956 МПа.
34. В Закрытом сосуде емкостью V = 0,3 м3 содержится 2,75 кг воздуха при давлении р1= 0,8 МПа и температуре t1 = 25 °С.
Определить давление и удельный объем после охлаждения воздуха до 0 ºС.
Отв. р2 = 0,732 МПа, 
= 0,109 м3/кг.
35. В закрытом сосуде находится газ при разрежении р1 = 2666 Па и температуре t1 = 100 ºС. Показание. барометра — 10 кПа. После охлаждения газа разрежение стало равным 20 кПа.
Определить конечную температуру газа t2.
Отв. t2 = -40,4 °С.
36. До какой температуры t2 нужно нагреть газ при = const, если начальное давление газа р1 = 0,2МПа и температура t1 = 20 °С, а конечное давление р2 = 0,5 МПа.
Отв. До t2 =459,5 °С.
37. В калориметрической бомбе емкостью 300 см3 находится кислород при давлении р1 = 2,6 МПа и температуре t1 = 22 °С.
Найти температуру кислорода t2 после подвода к нему теплоты в количестве 4,19 кДж, считая зависимость теплоемкости от температуры линейной.
Отв. t2 = 593 °С.
38. 0,2 м3 воздуха с начальной температурой 18 °С подогревают в цилиндре диаметром 0,5 м при постоянном давлении р = 0,2 МПа до температуры 200 °С.
Определить работу расширения перемещение поршня и количество затраченной теплоты, считая зависимость теплоемкости от температуры линейной.
Отв. L=25000 Дж; h = 0,64 м; Q =88,3 кДж.
39. Для использования отходящих газов двигателя мощностью N = 2500 кВт установлен подогреватель, через который проходит 60000 м3/ч воздуха при температуре t1 = 15 ºС и давлении р= 0,101 МПа. Температура воздуха после подогреватёля равна 75 °С.
Определить, какая часть теплоты топлива использована в подогревателе? К. п. д. двигателя принять равным 0,33. Зависимость теплоемкости от температуры считать линейной.
Отв. 17,4%.
40. К 1 м3 воздуха, находящемуся в цилиндре со свободно движущимся нагруженным поршнем, подводится при постоянном давлении 335 кДж теплоты. Объем воздуха при этом увеличивается до 1,5 м3. Начальная температура’ воздуха равна 15 °С.
Какая устанавливается в цилиндре температура, и какова работа расширения? Зависимость теплоемкости от температуры считать линейной.
Отв. t2 = 159 °С; L = 95,1 кДж.
41. 2 м3 воздуха с начальной. температурой t1 = 15 ºС расширяются при постоянном, давлении до 3 м3 вследствие сообщения газу 837 кДж теплоты.
Определить конечную температуру, давление газа в процессе и работу расширения.
Отв. t2 = 159 °С; р = 0,24 МПа; L = 239кДж.
42. Отходящие газы котельной установки проходят через воздухоподогреватель. Начальная температура газов tг1 = 300 °С, конечная tг2 = 160 °С; расход газов равен 1000 кг/ч. Начальная- температура воздуха составляет tв1 = 15 °С, а расход его равен 910 кг/ч.
Определить темпёратуру нагретого воздуха tв2, если потери воздухоподогревателя составляют 4%.
Средние теплоемкости (срm) для отходящих из котла газов и воздуха принять соответственно равными 1,0467 и 1,0048 кДж/(кг К).
Отв. tв2 = 168,9 °С.
43. В цилиндре двигателя внутреннего сгорания находится воздух при температуре 500 °С. Вследствие подвода теплоты, конечный объем воздуха увеличился в 2,2 раза. В процессе расширения воздуха давление в цилиндре практически оставалось постоянным.
Найти конечную температуру воздуха и удельные количества теплоты и работы, считая зависимость теплоемкости от температуры нелинейной.
Отв. t2 = 1428 ºС; qp = 1088,7 кДж/кг; l = 266,3 кДж/кг.
44. Воздух, выходящий из компрессора с температурой 190 °С, охлаждается в охладителе при постоянном давлении р = 0,5 МПа до температуры 20 °С. При этих параметрах производительность компрессора: равна 30 м3/ч.
Определить часовой расход охлаждающей воды, если она нагревается на 10 °С.
Отв. 733 л/ч.
45. Газовая смесь имеющая следующий массовый состав СО2 = 14%; 02 = 6%; N2 = 75% Н2О = 5% нагревается при постоянном давлении от t1 = 600 °С до t2 = 2000 °С.
Определить количество теплоты, подведенное к 1 кг газовой смеси. Зависимость теплоёмкости от температуры принять нелинейной.
Отв. qp = 1841 кДж/кг.
46. При сжигании в топке парового котла каменного угля объем продуктов сгорания составляет Vн = 11,025 м3/кг.
Анализ продуктов сгорания показывает следующий их объёмный состав СО2 = 10,3%; 02 = 7,8%; N2 = 75,3%; H2O = 6,6%.
Считая количество и состав продуктов сгорания неизменным по всему газовому тракту парового котла, а зависимость теплоемкости от температуры нелинейной определить количество теплоты, теряемой с уходящими газами (на 1 кг топлива), если на выходе из котла температура газов равна 180 °С, а температура окружающей среды 20 °С. Давление продуктов сгорания принято равным атмосферному.
Отв. qух = 2418 кДж/кг.
Пример. 1 кг воздуха при температуре t1 = 30 °С и начальном давлении р1 =0,1 МПа сжимается изотермическидо конечного давления р2= 1 МПа.
Определить конечный объём, затрачиваемую работу и количество теплоты, отводимой от газа.
Р е ш е н и е
Найдём начальный объём воздуха из уравнения состояния:
м3/кг
Так как в изотермическом процессе
,
то конечный объём
м3/кг
Работа, затрачиваемая на сжатие 1 кг воздуха, получается из уравнения:
кДж/кг
Количество теплоты, отводимой от газа, равно работе, затраченной на сжатие. Следовательно,
м3/кг
47. Воздух при давлении р1= 0,1 МПа и температуре t1 = 27 °С сжимается в компрессоре до р2 = 3,5 МПа.
Определить величину работы L затраченной на сжатие 100 кг воздуха, если воздух сжимается изотермически.
Отв. L = -30576 кДж.
48. Для осуществления изотермического сжатия 0,8 кг воздуха при р1 = 0,1 МПа и t = 25 °С затрачена работа в 100 кДж.
Найти давление р2 сжатого воздуха и количество теплоты, которое необходимо при этом отвести от газа?
Отв. р2 =0,322 МПа; Q = - 90 кДж.
49. Воздуху в количестве 0,1 м3 при р1 = 1 МПа и t1 = 200 °С сообщается 125 кДж теплоты; температура его при этом не изменяется.
Определить конечное давлениё р2, конечный объем V2 и получаемую работу L.
Отв. р2 = 0,286 МПа; V2 = 0,35 м3; L = 125 кДж.
50. При изотермическом сжатии 0,3 м3 воздуха с начальными параметрами р1 = 1 МПа и t1 = 300 °С отводится 500.кДж теплоты.
Определить конечный объем V2 и конечное давление p2.
Отв. V2 = 0,057 м3; р2 = 5,26 МПа.
51. При изотермическом сжатии 2,1 м3 азота, взятого при р1 = 0,1 МПа, от газа отводится 335 кДж теплоты.
Найти конечный объем V2, конечное давление р2 затраченную работу L.
Отв. V2 =0,426 м3; р2 = 0,49 МПа; L = -335 кДж.
52. В воздушный двигатель подается 0,0139 м3/с воздуха при р1 = 0,5 МПа и t1 = 40 °С.
Определить мощность, полученную при изотермическом расширении воздуха в машине, если р2 = 0,1 МПа.
Отв. L = 11,188 кВт.
53. 0,5 м3 кислорода при давлении р1 = 1 МПа и температуре t1 = 30 ºС сжимаются изотермически до объема в 5 раз меньше начального.
Определить объём и давление кислорода после сжатия, работу сжатия и количество теплоты, отнятого у газа.
Отв. р2 = 5 МПа; V2 = 0,1 м3; L = - 805 кдж.
54. 10 кг воздуха при давлении р1 = 0,12 МПа и температуре t1 = 30ºС сжимаются изотермически; при этом в результате сжатия объём уменьшается в 2,5 раза.
Определить начальные и конечные параметры, количество теплоты, работу и изменение внутренней энергии.
Отв. V1 = 7,25 м3; V2 = 2,9 м3; р2 = 0,3 МПа;
Q = L = - 797 кДж; ΔU = 0.
55. 1 кг воздуха при температуре t1 = 15 °С и начальном давлении р1 = 0,1 МПа адиабатно сжимается до 0,8 МПа.
Найти работу, конечный объём и конечную температуру.
Отв. t2 = 248 °С; υ2= 0,187 м3/кг; 1 = - 167,2 кДж/кг.
56. Воздух при давлении р1 = 0,45 МПа, расширяясь адиабатно до 0,12 МПа, охлаждается до t2 = - 45 °С.
Определить начальную температуру и работу совершённую 1 кг воздуха.
Отв. t1 = 61 °С; 1 = 75,3 кДж/кг.
57. 1 кг воздуха, занимающий объем υi = 0,0887 м3/кг при рi = 1 МПа, расширяется до 10-кратного объема.
Получить конечное давление и работу, совершенную воздухом, в изотермическом и адиабатном процессах.
Отв. 1) Т = const; p2 = 0,1 МПа; l = 204кДж/кг;
2) dQ = 0; р2 = 0,04 МПа; l = 133,5 кДж/кг.
58. Воздух при температуре t1= 250 ºС адиабатно охлаждается до t2 = -55 °С; давление при этом падает до 0,1 МПа.
Определить начальное давление и работу расширения 1 кг воздуха.
Отв. р1 = 0,3 МПа; 1 = 57,4 кДж/кг.
59. 0,8 м3 углекислого газа при температуре t1 = 20 °С и давлении рi = 0,7 МПа адиабатно расширяются до трехкратного объема.
Определить конечные параметры р2 и t2 и величину полученной работы L (k принять равным 1,28).
Отв. р2 = 0,17 МПа; t2 = - 57,6 °С; L = 535,7 кДж.
60. До какого давления нужно адиабатно сжать смесь воздуха и паров бензина, чтобы в результате повышения температуры наступило самовоспламенение смеси?
Начальные параметры: p1 = 0,1 МПа, t1 = 15 °С. Температура воспламенения смеси t2 = 550 °С; k = 1,39.
Отв. р2 = 4,2 МПа.
61. Работа, затраченная на адиабатное сжатие З кг воздуха, составляет 471 кДж. Начальное состояние воздуха характеризуется параметрами: t1 = 15 °С; р1= 0,1 МПа.
Определить конечную температуру и изменение внутренней энергии.
Отв. t2 = 234 °С; ΔU = - 471 кДж.
62. В цилиндре газового двигателя находится газовая смесь при давлении p1 = 0,1 МПа и температуре t1= 500 °С. Объем камеры сжатия двигателя составляет 16% от объема, описываемого поршнем.
Определить конечное давление и конечную температуру газовой смеси при адиабатном ее сжатии. Показатель адиабаты принять равным 1,38.
Отв. pi = 1,54 МПа; t2 = 412 °С.
63. В двигателе с воспламенением, от сжатия воздух сжимается таким образом, что его температура поднимается выше температуры воспламенения нефти.
Какое минимальное давление должен иметь воздух в конце процесса сжатия, если температура воспламенения нефти равна 800 °С? Во сколько раз при этом уменьшится объем воздуха?
Начальное давление воздуха. р1 = 0,1 МПа, начальная температура воздуха t1 = 80 °С. Сжатие воздуха считать адиабатным.
Отв. p2 = 4,9 МПа; ε = 
= 16.
64. Объем воздуха при адиабатном сжатии в цилиндре двигателя внутреннего сгорания уменьшается в 13 раз. Начальная температура воздуха перед сжатием t1 = 770 °С, а начальное давление p1= 0,09 МПа.
Определить температуру и давление воздуха после сжатия.
Отв. t2 = 7030 °С; p2 = 3,27 МПа.
65. 2 кг воздуха при давлении p1 = 0,1 МПа; t1 = 15° С адиабатно сжимаются в цилиндре компрессора до давления pЗ = 0,7 МПа.
Найти конечную температуру сжатого воздуха и работу, затраченную на сжатие.
Отв. t2 = 229 °С;.L = - 307,1 кДж.
66. 1 м3 воздуха при, давлении 0,095 МПа и начальной температуре 10 °С сжимается по адиабате до 0,38 МПа.
Определить температуру и объем воздуха в конце сжатия и работу, затраченную на сжатие.
Отв. t2 = 148 °С; V2=0,373 м3, L = - 117,5 кДж.
67. Воздух при температуре 127 °С изотермически сжимается так, что объем его становится равным 1/4 начального, а затем расширяется по адиабате до начального давления.
Найти температуру воздуха в конце адиабатного расширения. Представить процесс расширения и сжатия воздуха в диаграмме рυ.
Отв. t2= - 4 °С.
68. 1 кг воздуха при температуре t1= 17 °С сжимается адиабатно до объема, составляющего 1/5 начального, а затем расширяется изотермически до первоначального объема.
Определить работу, произведенную воздухом в результате обоих процессов.
Отв. l = 67 кДж/кг.
69. Воздух при температуре t1 = 20 °С должен быть охлажден посредством адиабатного расширения до температуры t2 = -60 °С. Конечное давление воздуха при этом должно составлять 0,1 МПа.
Определить начальное давление воздуха p1 и удельную работу расширения l.
Отв. р1= 0,3 МПа; l = 57,8 кДж/кг.
70. Воздух в количестве 3 м3 расширяется политропно от р1=0,54 МПа и t1 =45 °С до p2 = 0,15 МПа. Объем, занимаемый при этом воздухом, становится равным 10 м3.
Найти показатель политропы, конечную температуру, полученную работу и количество подведенной теплоты.
Отв. n = 1,064; t2=21,4 °С; L=1875 кДж; Q = 1575 кДж.
71. В цилиндре двигателя с изобарным подводом теплоты сжимается воздух по политропе с показателем n = 1,33.
Определить температуру и давление воздуха в конце сжатия, если степень сжатия (ε = ) равна 14, t1= 77 °С и p1 = 0,1 МПа.
Отв.t2= 564 °С; p2 = 3,39 МIIа.
72. В процессе политропного сжатия затрачивается работа, равная 195 кДж, причем в одном случае от газа отводится 250 кДж, а в другом - газу сообщается 42 кДж.
Определить показатели обеих политроп.
Отв. 1) n = 0,9; 2) n = 1,49.
73. 1,5 м3 воздуха сжимаются от 0,1 МПа и 17 °С до 0,7 МПа; конечная температура при этом равна 100 °С.
Какое количество теплоты требуется отвести, какую работу затратить и каков показатель политропы?
Отв. Q = -183 кДж; L = -290 кДж; n = 1,147.
74. Горючая смесь в. цилиндре двигателя, имеющая температуру t1 = 100 °С и давление p1 =0,09 МПа; подвергается сжатию по политропе с показателем n = 1,33.
Определить конечное давление и степень сжатия в момент, когда темпёратура достигнет 400 °С.
Отв. ε = 5,9; р2 = 0,95 МПа.
75. В процессе политропного расширения воздуху сообщается 83,7 кДж теплоты.
Найти изменение внутренней энергии воздуха и произведенную работу, если объем воздуха увеличился в 10 раз, а давление его уменьшилось в 8 раз.
Отв. ΔU = 16,7 кДж; L = 6702 кДж.
76. Воздух расширяется по политропе, совершая при этом работу, равную 270 кДж, причем в одном случае ему сообщается 420 кДж теплоты, а в другом от воздуха отводится 92 кДж теплоты
Определить в обоих случаях показатели политропы.
Отв. 1) n = 0,7;, 2) n = 1,88.
77.Смесь коксового газа с воздухом сжимается по политропе с показателем n = 1,38; начальное давление р1 = 0,1 МПа, начальная температура t1 = 50 °С.
Определить конечную температуру и давление, если степень сжатия ε= 4.
Отв. t2= 276 °С; р2 = 0,68 МПа.
78. В газовом двигателе политропно сжимается горючая смесь [R=340 дж/(кг·К)] до температуры 450 °С. Начальное давление смеси p1=0,09 МПа, начальная температура t1= 80 °С. Показатель политропы n =1,35.
Найти работу сжатия и степень сжатия.
Отв. l = -360 кДж/кг; ε = 7,82.
79. 2м3 воздуха при давлёнии р1 = 0,2 МПа и температуре t1 = 400 °С сжимаются до давления p2 = 1,1 МПа и объема V2 = 0,5 м3.
Определить показатель политропы, работу сжатия и количество отведенной теплоты.
Отв. n = 1,23; L = - 652 кДж; Q = -272 кДж.
80. Находящийся в цилиндре двигателя внутреннего сгорания воздух при давлении p1 = 0,09 МПа и t1 = 100 °C должен быть так сжат, чтобы конечная температура его поднялась до 650 °С.
Определить, какое должно быть отношение объема камеры сжатия двигателя к объему, описываемому поршнем, если сжатие происходит по политропе с показателем n = 1,3.
Отв. V2=0,0512Vh
81. 1 кг воздуха при давлении р1 = 0,4 МПа и температуре t1 = 100 °С расширяется до давления р2 = 0,1 МПа.
Найти конечную температуру, количество теплоты и совершенную работу, если расширение происходит:
а) изохорно, б) изотермически, в) адиабатно и г) политропно с показателем m = 1,2.
Отв. а) t2 = -180 °С; l = 0;q = -202 кДж/кг;
б) t2 = t1, l = 148,2 кДж/кг; q = 148,2 кДж/кг;
в) t2 = -22 °С; l = 87,5 кДж/кг; q = 0;
г) t2 = 24 °С; l = 10,9 кДж/кг, q = 54,5 кДж/кг.
82. Найти приращение энтропии 3 кг воздуха; а)при нагревании его по изобаре от 0 до 400 °С; 6) при нагревании его по изохоре от 0° до 880 °С; в) при изотермическом расширении с увеличением объема в 16 раз. Теплоемкость считать постоянной.
Овт. а) Δsp = 2,74 кДж/К.; 6) Δsυ = 3,13 кДж/К;
в) Δsr. = 2,36 кДж/К.
83. 1 кг воздуха сжимается по политропе от 1 МПа и 20 °С до 0,8 МПа при n = 12.
Определить конечную температуру, изменение энтропии, количество отведенной теплоты и затраченную работу.
Отв. t2 = 141 °С; Δs = 0,2445 кДж/(кг. К);
q = -87,1 кДж/кг; l = 173,0 кДж/кг.
84. В сосуде объемом 400 л заключен воздух при давлении р1 = 0,1 МПа и температуре p1 = - 40 °С. Параметры среды: рo = 0,1 МПа и to = 200 °С.
Определить максимальную полезную работу, которую может. произвести воздух, заключенный в сосуде. Представить процесс в. диаграммах р,υ и T,s.
Отв. L max(полезн) = 4600 Дж.
Пример. Найти. энтропию 1 кг кислорода при р = 0,8 МПа и t = 250° С. Теплоемкость считать переменной, приняв зависимость ее от температуры линейной.
Р е ше н и е
По формуле
Из таблицы IV для кислорода
кДж/(кг К),
Поэтому формула линейной зависимости истенной теплоёмкости будет иметь вид
кДж/(кг К),
или
кДж/(кг К),
следовательно
Таким образом,
значение энтропии
;
кДж/(кг К),
Пример. 1 кг воздуха совершает цикл Карно в пределах температур t1 = 627°С и t2 = 27°С, причем наивысшее давление составляет 6 МПа, а наинизшее 0,1 МПа.
Определить параметры состояния воздуха в характерных точках, цикла, работу, термический к. п. д. цикла и количество подведённой и отведённой теплоты.
Р е ш е н и е
Точка 1.
р1 = 6 МПа; Т1 = 900 К.
Удельный объём газа находим из характеристического уравнения
м3/кг
Точка 2.
Т2 = 900 К.
Из уравнения адиабаты (линия 2—3)
;
Из уравнения изотермы (линия 1—2)
получаем
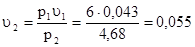м3/кг
Точка 3.
Р3 = 0,1 МПа; Т3 = 300 К
м3/кг
Точка 4.
Т4 = 300 К
Из уравнения адиобаты (линия 4 – 1) имеем
МПа.
Из уравнения изотермы (линия 3 – 4) получаем
;
м3/кг
Термический к.п.д. цикла
Подведённое количество теплоты
кДж/кг
Отведённое количество теплоты
кДж/кг
Работа цикла
кДж/кг
Для проверки можно воспользоваться формулой
85. 1 кг воздуха совершает цикл Карно между температурами t1 = 327 °С и t2 = 27 °С; наивысшее давление при этом составляет 2 МПа, а наинизшее – 0,12 МПа.
Определить параметры состояния воздуха в характерных точках, работу, термический к. п. д. цикла и количества подведенной и отведенной теплоты.
Отв. υ1= 0,861 м3/кг; υ2= 0,127 м3/кг; υ3= 0,717 м3/кг;
υ4 = 0,486 м3/кг; p2 = 1,36 МПа; р4 = 0,18 МПа; ηt = 0,5;
l0 = 33,7 кДж/кг; q1 = 67,4 кДж/кг, q2 = 33,7 кДж/кг.
86. 1 кг воздуха совершает цикл Карно в пределах температур t1 = 250 °С и t2 = 30 °С. Наивысшее давление p1 =1 МПа, наинизшее – р3 = 0,12 МПа.
Определить параметры состояния воздуха в характерных точках, количество подведённой и отведённой теплоты, работу и термический к.п.д. цикла.
Отв. υ1 = 0,15 м3/кг; υ2 = 0,185 м3/кг; υ3 = 0,725м3/кг;
υ4 = 0,59 м3/кг; p2 = 0,81 МПа; р4 = 0,15 МПа; ηt = 0,42;
l0 = 18,1 кДж/кг; q1 = 31,1 кДж/кг, q2 = 18 кДж/кг.
87. Поршневой двигатель работает на воздухе по циклу с подводом теплоты при υ = const. Начальное состояние воздуха: р1 = 0,785 МПа и t1= 17 °С. Степень сжатия ε = 4,6. Количество подведенной теплоты составляет 100,5 кДж/кг.
Найти термический к. п. д. двигателя и его мощность, если диаметр цилиндра d = 0,24 м, ход поршня S = 0,34 м, число оборотов n = 21 рад/с (200 об/мин) и за каждые два оборота совершается один цикл.
Отв. ηt = 0,457; N = 14,5 кВт.
88. Температура воспламенения топлива, подаваемого в цилиндр двигателя с изобарным подводом теплоты, равна 800 °С.
Определить минимально необходимое значение степени сжатия ε, если начальная температура воздуха t1 = 77 °С. Сжатие считать адиабатным, k = 1,4.
Отв. ε = 16,4.
89. Для цикла поршневого двигателя внутреннего сгорания с подводом теплоты при р = const определить параметры в характерных точках, полезную работу, количество подведенной и отведенной теплоты и термический к. п. д., если дано: р1 = 100 кПа, t1 = 70 °С; ε = 12; k = 1,4; ρ = 1,67. Рабочее тело — воздух. Теплоёмкость принять постоянной.
Отв. υ1 = 0,98 м3/кг; υ2 = 0,082 м3/кг; υ3 = 0,14 м3/кг;
р2 = 3,24 МПа; р4 = 0,2 МПа; q1 = 627 кДж/кг;
q2 = 255 кДж/кг; l0 = 372 кДж/кг; ηt = 0,593.
90. Найти давление и объем в характерных точках цикла поршневого двигателя внутреннего сгорания с подводом теплоты при р = const, а также термический к. п. д.и полезную работу, если дано: р1 =100кПа, ε = 14; ρ = 1,5; k = 1,4.
Диаметр цилиндра d = 0,3 м, ход поршня S = 0,45 м. Рабочее тело — воздух. Теплоёмкость считать постоянной.
Отв. V1 = V4 = 0,03416 м3; V2 = 0,00244 м3;V3 = 0,00366 м3;
р2 = 4,02 МПа; р4 =0,176 МПа, ηt = 0,65.
91. В цикле с подводом теплоты при р = const начальное давление воздуха р1 =0,09 МПа, температура t1 = 47 °С, степень сжатия ε = 12, степень предварительного расширения ρ = 2 и k = 1 м3.
Определить параметры в характерных точках цикла, количество подведенной и отведенной теплоты, работу цикла и его термический к. п. д. Рабочее тело — воздух. Теплоёмкость принять постоянной.
Отв. V2 = 0,0832 м3; V3 = 0,166 м3; р2 = 2,92 МПа;
р4 = 0,24 МПа; T2 = 865 К; Т3 = 1730 К; Т4 = 845 К;
L0 = 478 кДж; Q1 = 842 кДж; Q2 = 364 кДж; ηt = 0,565.
92. Рабочее тело поршневого двигателя внутреннего сгорания со смешанным подводом теплоты обладает свойствами воздуха. Известны начальные параметры р1 = 0,1 МПа, t1 = 30° С и следующие характеристики цикла; ε = 7, λ = 2,0 и ρ = 1,2.
Определить параметры в характерных для цикла точках, количество подведенной теплоты, полезную работу и термический к. п. д. цикла. Рабочее тело—воздух. Теплоемкость считать постоянной.
Отв. υ1 = 0,870 м3/кг; υ2 = 0,124 м3/кг; υ4 = 0,149 м3/кг;
р2 = 1,52 МПа; p3 = 3,05 МПа; р5 = 0,26 МПа;
t2 = 387 °С; t3 = 1047 °С; t4 = 1311 °С;
t5 = 511 °С; q1 = 744,2 кДж/кг; q2 = 348,2 кДж/кг;
l0 = 396 кДж/кг; ηt = 0,532.
93. Для идеального цикла газовой турбины с подводом теплоты при р = const определить параметры в характерных точках, полезную работу, термический к. п. д., количество подведенной и отведенной теплоты. Дано: p1 = 0,1 МПа; t1 = 17 °С; t3 = 600 °С; λ = p2/p1 = 8. Рабочее тело — воздух. Теплоемкость принять постоянной.
Отв. υ1 = 0,831 м3/кг; υ2 = 0,189м3/кг; υ3 = 0,313 м3/кг;
υ4 = 1,38 м3/кг; t2 = 254 °С; р2 = р3 = 0,8 МПа;
q1 = 350 кДж/кг; q2 = 192,2 кДж/кг; ηt = 0,45.
94. Газовая турбина работает по циклу с подводом теплоты при р = const. Известны параметры; p1 = 0,1 МПа; t1 = 40 °С; t4 = 400 °С, а также степень увеличения давления λ = 8. Рабочее тело — воздух.
Определить параметры в характерных точках цикла, количество подведенной и отведенной теплоты, работу, совершаемую за цикл, и термический к. п. д. Теплоемкость считать постоянной.
Отв. υ1 = 0,9 м3/кг; р2 = 0,8 МПа; υ2 = 0,204 м3/кг;
t2 = 297 °С; υ3 = 0,438 м3/кг; t3 = 948 °С;
υ4 = 1,93 м3/кг; q1 = 659 кДж/кг
q2 = 364 кДж/кг; l0 = 296 кДж/кг; ηt = 0,45.
95. Газовая турбина работает по циклу с подводом тепла при р = const без регенерации. Известны степень повышения давления в цикле λ = p2/р2 =7 и степень предварительного расширения ρ = υ3/υ 2 = 2,4. Рабочее тело — воздух.
Найти термический к. п. д. этого цикла и сравнить его с циклом поршневого двигателя внутреннего сгорания с подводом теплоты при р = const при одинаковых степенях сжатия е и при одинаковых степенях расширения р. Представить цикл в диаграмме Ts.
Отв. ηt гт = 0,426; ηt п.д== 0,297.
96. Газотурбинная установка работает с подводом теплоты при υ = const и с полной регенерацией. Известны параметры: t1= 30 °С и t5 = 400 °С, а также λ = =p2/p1 =4. Рабочее тело — воздух.
Определить термический к. п. д. этого цикла. Изобразить цикл в диаграмме Ts.
Отв. ηt ре = 0,585.
97. Компрессор всасывает 250 м3/ч воздуха при р1= 0,09 МПа и t1 = 25 °С и сжимает его до р2 = 0,8 МПа.
Какое количество воды нужно пропускать через рубашку компрессора в час, если сжатие происходит политропно с показателем n = 1,2 и температура воды повышается на 15 °С?
Отв. 390 л/ч.
98. Компрессор всасывает 120 м3/ч воздуха при p1 = 0,1 МПа и t1 = 27 °С и сжимает его до р2 = 1,2 МПа.
Определить; а) температуру сжатого воздуха при выходе из компрессора; б) объем сжатого воздуха; в) работу и мощность, расходуемые на сжатие воздуха.
Расчет произвести для изотермического, адиабатного и политропного сжатия воздуха. Показатель политропы принять равным 1,3.
Отв. a) t2 = t1; V2 = 10 м3/ч; L0 = 29,8 МДж/ч; N = 8,3 кВт;
б) t2 = 339 °С; V2 = 20,4 м3/ч; L0 = 43,4 МДж/ч; N = 12 кВт;
в) t2 = 257 °С; V2 = 17,7 м3/ч; L0 = 40,2 МДж/ч; N = 11,2 кВт.
99. Компрессор всасывает в минуту 100 м3 водорода при температуре 20 °С и давлении 0,1 МПа и сжимает его до 0,8 МПа.
Определить потребную мощность двигателя для привода компрессора при адиабатном сжатии, если эффективный к.п.д. компрессора ηt = 0,7.
Отв. N = 678 кВт.
100. Приемные испытания компрессоров обычно проводятся не на газе, на котором должен работать компрессор, а на воздухе.
Для условий предыдущей задачи найти потребную мощность двигателя при работе компрессора на воздухе. Сравнить полученные результаты.
Отв. N = 678 кВт.
101. Через пароперегреватель парового котла проходит 5000 кг пара в час. Степень сухости пара до пароперегревателя х = 0,99, а давление р = 10 МПа. Температура пара после пароперегревателя t = 550 °С.
Определить количество теплоты, воспринятой пароперегревателем, принимая его к.п.д. равным 0,984.
Отв. Q = 4,0 ГДж/ч.
102. Паровой котел имеет паропроизводительность 20 кг/с. Рабочее давление пара р = 4 МПа, а температура его t = 440 °С. Теплота сгорания топлива равна 12600 кДж/кг; температура питательной воды tпв = 145 °С.
Определить к.п.д. котла, если расход топлива составляет 4,89 кг/с.
Отв. ηк = 0,875.
103. Паровые котлы высокого давления Таганрогского завода «Красный котельщик» имеют паропроизводительность 640 т/ч при давлении пара р = 132 МПа и температуре t = 570 °С. Температура питательной воды tв= 230 °С. Теплота сгорания топлива составляет 25120 кДж/кг.
Чему равен часовой расход топлива, если к.п.д. парового котла составляет 87,6 %?
Отв. 73364 кг/ч.
104. Паровая машина с приводом для заводских целей, созданная талантливым русским ученым изобретателем И. И. Ползуновым, имела следующие размеры: диаметр цилиндра 0,81 м и ход поршня 2,56 м. Давление пара, поступающего в машину, составляло 0,118 МПа.
Считая пар, поступающий в машину, влажным насыщенным со степенью сухости х = 0,97, определить массу пара в цилиндре машины.
Отв. М = 0,935 кг.
105. Найти диаметр паропровода, по которому протекает пар при давлении р = 1,2 МПа и температуре t = 260 °С. Расход пара М =350 кг/ч, скорость пара w = 50 м/с.
Отв. d = 22,1 мм.
106. Определить диаметр паропровода, по которому протекает пар при давлении р = 1,8 МПа. Расход пара М = 1,11 кг/с, скорость пара w = 20 м/с. Произвести расчет для трех случаев; 1) х 1= 0,9; 2) хг = 1; 3) t == 340 °С.
Отв. 1) d = 84 мм; 2) d = 88 мм; 3) d = 104 мм.
107. В паровом котле объемом V = 15 м3 находятся 4000 кг воды и пара при давлении 4 МПа и температуре насыщения.
Определить массы воды и сухого насыщенного пара, находящиеся в котле.
Отв. Мп = 206 кг; Мв = 3794 кг.
108. В паровом котле находятся 25 м3 воды при давлении 3,5 МПа и температуре насыщения.
Какое количество пара по массе и объему образовалось бы в котле, если бы давление в нем упало до 0,1 МПа?
Отв. М = 5651 кг; V = 9607 м3.
109. В пароперегреватель парового котла поступает пар в количестве D = 20 т/ч при давлении р = 4 МПа и со степенью сухости х =0,98. Количество теплоты, сообщенной пару в пароперегревателе, составляет 11313 МДж/ч.
Определить температуру пара на выходе из пароперегревателя. Потерями давления в нем пренебречь, считая процесс изобарным.
Отв. tne = 450 °С.
110. К 1 кг пара при давлении 0,8 МПа и степени влажности 70% подводится при постоянном давлении 820 кДж теплоты.
Определить степень сухости, объём и энтальпию пара в конечном состоянии.
Отв. х2 =0,7; υ2 = 0,1682 м3/кг; i2 = 2154,4 кДж/кг.
111. 1 кг влажного пара при давлении 1,8 МПа и влажности 3% перегревается при постоянном давлении до t = 400 °С.
Определить работу расширения, количество сообщенной теплоты и изменение внутренней энергии.
Отв. l = 110,2 кДж/кг; q = 500 кДж/кг; Δu = 390 кДж/кг.
112. 1 м3 водяного пара при давлении p1 = 1 МПа и х = 0,65 расширяется при р = const до тех пор, пока его удельный объем не станет равным υ2= 0,19 м3/кг.
Найти конечные параметры, количество теплоты, участвующей в процессе, работу и изменение внутренней энергии.
Отв. х2 = 0,96; Q = 5196 кДж; L = 581,4 кДж; ΔU = 4614,6 кДж.
113. 1,2 м3 влажного пара со степенью сухости х = 0,8 расширяется адиабатно от 0,4 до 0,06 МПа.
Определить степень сухости, объем пара в конце расширения и произведенную им работу.
Отв. х = 74 %; V2 = 6,56 м3; L = 743 кДж.
114. Найти по диаграмме is адиабатный перепад теплоты и конечное состояние при расширении пара от 1,4 МПа и 300 °С до 0,006 МПа.
Отв. h = 900 кДж/кг; х = 0,825.
115. Пар с начальным давлением p1 = 2 МПа и температурой t1 = 300 °С расширяется адиабатно до р2 = 0,004 МПа.
Определить начальные и конечные параметры и работу расширения 1 кг пара.
Отв. l1 = 3019 кДж/кг; υ1 = 0,1255 м3/кг; i2 = 2036 кДж/кг; х = 0,787;
l = 842 кДж/кг.
116. Пар с начальным давлением pi = 1,8 МПа и температурой t1= 340 °С расширяется адиабатно до давления p2 = 0,006 МПа.
Определить работу расширения и конечное состояние пара.
Отв. l = 815 кДж/кг; р2 = 19,5 м3/кг; х2 = 0,825.
117. 1 кг пара при давлении р1 = 5 МПа и температуре t1 = 400 °С расширяется по адиабате до давления 0,05 МПа.
Найти, пользуясь диаграммой is-, температуру и степень сухости для конечного состояния пара, а также адиабатный перепад теплоты.
Отв. t2 = 80 °С; х2 = 0,853; h0 = 888 кДж/кг.
118. 5 кг водяного пара, параметры которого p1 = 2 МПа и V1 = 0,5 м3, расширяются адиабатно до давления р2 = 0,2 МПа.
Определить конечный объем пара, степень сухости его и произведённую им работу.
Отв. V2 = 3,95 м3; х2 = 0,852; L = 1780 кДж.
119. Определить теоретическую скорость истечения пара из котла в атмосферу. Давление в котле р = 0,15 МПа и х = 0,95, Процесс расширения пара считать адиабатным.
Отв. с = 360 м/с.
120. Влажный пар с. параметрами р1 = 1,8 МПа и x1 = 0,92 вытекает в среду с давлением р2 = 1,2 МПа; площадь выходного сечения сопла f == 20 мм2.
Определить теоретическую скорость при адиабатном истечении пара и его секундный расход.
Отв. w = 380 м/с; М = 0,05 кг/с.
121. Найти теоретическую скорость истечения пара из сопла Лаваля для следующих данных: р1 = 1,6 МПа, t1 = 300 °С, р2 = 0,1 МПа. Процесс расширения пара в сопле считать адиабатным.
Отв. w = 1040 м/с.
122. Пар при давлении p1 = 10 МПа и t1 = 320 °С дросселируется до р2=3МПа.
Определить параметры конечного состояния и изменение температуры пара.
Отв. х2= 0,99; Δt = 85 °С.
123. Отработавший пар из паровой турбины поступает в конденсатор в количестве 125 т/ч. Состояние отработавшего пара р2 = 0,0045 МПа и х = 0,89.
Определить диаметр входного патрубка конденсатора, если скорость пара в нем до = 120 м/с.
Omв. d = 3,22 м.
124. В паровую турбину подается пар со следующими параметрами: p1 = 5,9 МПа, t1 = 400 °С. В клапанах турбины пар дросселируется до 5,4 МПа и поступает в расширяющиеся сопла, давление за которыми р2 = 0,98 МПа. Расход пара через одно сопло М = 8000 кг/ч. Скоростной коэффициент φ= 0,94.
Определить площади минимального и выходного сечений.
Отв. fmln = 355 мм2; fmax = 546 мм2.
125. На электростанции сжигается топливо с теплотой сгорания Qнр=30 МДж/кг.
Определить удельный расход топлива на 1 кВт·ч, если известны следующие данные; ηк у =0,8; ηя = 0,97; ηt= 0,4; ηoi= 0,82; ηм= 0,98; ηг = 0,97.
Определить также удельный расход теплоты на 1 кВт·ч.
Отв. q= 14,9 МДж/(кВт·ч); b = 0,498 кг/(кВт·ч).
126. Паровая турбина мощностью N = 25 МВт работает при начальных параметрах p1 = 3,5 МПа и t1 == 400 °С. Конечное давление пара р2 = 0,004 МПа.
Определить часовой расход топлива при полной нагрузке паровой турбины, если к.п.д. котельной установки ηку = 0,82, теплота сгорания топлива Qнр = 41870кДж/кг, а температура питательной воды tпв = 88 °С. Считать, что турбина работает по циклу Ренкина.
Отв. В = 6430 кг/ч.
127. Турбины высокого давления мощностью N = 100000 кВт работают на паре при р1 = 9 МПа и t1 = 480 °С, р2 = 0,004 МПа. Определить термический к.п.д. цикла Ренкина для данных параметров, и достигнутое улучшение термического к.п.д. по сравнению с циклом Ренкина для параметров пара: p1 = 2,9 МПа, t1=400 °С; р2= 0,004 МПа.
Отв. ηt = 42, 1%; ε = 14,4%.
128. Паротурбинная установка мощностью N = 200 МВт работает по циклу Ренкина при начальных параметрах р1 = 13 МПа и t1 = 565 °С. При давлении р' = 2 МПа осуществляется промежуточный перегрев пара до первоначальной температуры. Давление в конденсаторе р2 = 0,004 МПа. Температура питательной воды tпв=160 °С.
Определить часовой расход топлива, если теплота сгорания топлива Qнр = 29,3 мДж/кг, а к.п.д. котельной установки ηку = 0,92.
Отв. В = 49624 кг/ч.
129. Проект паротурбинной установки предусматривает следующие условия ее работы: р1 = 30 МПа, t1 = 550 °С; р2 = 0,1 МПа. При давлении р' = 7 МПа вводится вторичный перегрев до температуры 540 °С,
Принимая, что установка работает по циклу Ренкина, определить конечную степень сухости пара при отсутствии вторичного перегрева и улучшение термического к.п.д. и конечную сухость пара после применения вторичного перегрева
Отв. х2 = 0,782; х3 = 0,928; ε = 3,65%.
130. В паровом котле находятся 25 м3 воды при давлении 3,5 МПа и температуре насыщения.
Какое количество пара по массе и объему образовалось бы в котле, если бы давление в нем упало до 0,1 МПа?
Отв. М = 5651 кг; V = 9607 м3.
131. В пароперегреватель парового котла поступает пар в количестве D = 20 т/ч при давлении р = 4 МПа и со степенью сухости х =0,98. Количество теплоты, сообщенной пару в пароперегревателе, составляет 11 313 МДж/ч.
Определить температуру пара на выходе из пароперегревателя. Потерями давления в нем пренебречь, считая процесс изобарным.
Отв. tne = 450 °С.
132. К 1 кг пара при давлении 0,8 МПа и степени влажности 70% подводится при постоянном давлении 820 кДж теплоты.
Определить степень сухости, объём и энтальпию пара в конечном состоянии.
Отв. х2 =0,7; υ2 = 0,1682 м3/кг; i2 = 2154,4 кДж/кг.
133. 1 кг влажного пара при давлении 1,8 МПа и влажности 3% перегревается при постоянном давлении до t = 400 °С.
Определить работу расширения, количество сообщенной теплоты и изменение внутренней энергии.
Отв. l = 110,2 кДж/кг; q = 500 кДж/кг; Δu = 390 кДж/кг.
134. 1 м3 водяного пара при давлении p1 = 1 МПа и х = 0,65 расширяется при р = const до тех пор, пока его удельный объем не станет равным υ2= 0,19 м3/кг.
Найти конечные параметры, количество теплоты, участвующей в процессе, работу и изменение внутренней энергии.
Отв. х2 = 0,96; Q = 5196 кДж; L = 581,4 кДж; ΔU = 4614,6 кДж.
135. 1,2 м3 влажного пара со степенью сухости х = 0,8 расширяется адиабатно от 0,4 до 0,06 МПа.
Определить степень сухости, объем пара в конце расширения и произведенную им работу.
Отв. х = 74 %; V2 = 6,56 м3; L = 743 кДж.
136. Найти по диаграмме is адиабатный перепад теплоты и конечное состояние при расширении пара от 1,4 МПа и 300 °С до 0,006 МПа.
Отв. h = 900 кДж/кг; х = 0,825.
137. Пар с начальным давлением p1 = 2 МПа и температурой t1 = 300 °С расширяется адиабатно до р2 = 0,004 МПа.
Определить начальные и конечные параметры и работу расширения 1 кг пара.
Отв. l1 = 3019 кДж/кг; υ1 = 0,1255 м3/кг; i2 = 2036 кДж/кг; х = 0,787;
l = 842 кДж/кг.
138. Пар с начальным давлением pi = 1,8 МПа и температурой t1= 340 °С расширяется адиабатно до давления p2 = 0,006 МПа.
Определить работу расширения и конечное состояние пара.
Отв. l = 815 кДж/кг; р2 = 19,5 м3/кг; х2 = 0,825.
139. 1 кг пара при давлении р1 = 5 МПа и температуре t1 = 400 °С расширяется по адиабате до давления 0,05 МПа.
Найти, пользуясь диаграммой is-, температуру и степень сухости для конечного состояния пара, а также адиабатный перепад теплоты.
Отв. t2 = 80 °С; х2 = 0,853; h0 = 888 кДж/кг.
140. 5 кг водяного пара, параметры которого p1 = 2 МПа и V1 = 0,5 м3, расширяются адиабатно до давления р2 = 0,2 МПа.
Определить конечный объем пара, степень сухости его и произведённую им работу.
Отв. V2 = 3,95 м3; х2 = 0,852; L = 1780 кДж.
141. Определить теоретическую скорость истечения пара из котла в атмосферу. Давление в котле р = 0,15 МПа и х = 0,95, Процесс расширения пара считать адиабатным.
Отв. с = 360 м/с.
142. Влажный пар с. параметрами р1 = 1,8 МПа и x1 = 0,92 вытекает в среду с давлением р2 = 1,2 МПа; площадь выходного сечения сопла f == 20 мм2.
Определить теоретическую скорость при адиабатном истечении пара и его секундный расход.
Отв. w = 380 м/с; М = 0,05 кг/с.
143. Найти теоретическую скорость истечения пара из сопла Лаваля для следующих данных: р1 = 1,6 МПа, t1 = 300 °С, р2 = 0,1 МПа. Процесс расширения пара в сопле считать адиабатным.
Отв. w = 1040 м/с.
144. Пар при давлении p1 = 10 МПа и t1 = 320 °С дросселируется до р2=3МПа.
Определить параметры конечного состояния и изменение температуры пара.
Отв. х2 = 0,99; Δt = 85 °С.
145. Отработавший пар из паровой турбины поступает в конденсатор в количестве 125 т/ч. Состояние отработавшего пара р2 = 0,0045 МПа и х = 0,89.
Определить диаметр входного патрубка конденсатора, если скорость пара в нем до = 120 м/с.
Omв. d = 3,22 м.
146. В паровую турбину подается пар со следующими параметрами: p1 = 5,9 МПа, t1 = 400 °С. В клапанах турбины пар дросселируется до 5,4 МПа и поступает в расширяющиеся сопла, давление за которыми р2 = 0,98 МПа. Расход пара через одно сопло М = 8000 кг/ч. Скоростной коэффициент φ= 0,94.
Определить площади минимального и выходного сечений.
Отв. fmln = 355 мм2; fmax = 546 мм2.
147. На электростанции сжигается топливо с теплотой сгорания Qнр = 30 МДж/кг.
Определить удельный расход топлива на 1 кВт·ч, если известны следующие данные; ηк у =0,8; ηп = 0,97; ηt= 0,4; ηoi= 0,82; ηм= 0,98; ηг = 0,97.
Определить также удельный расход теплоты на 1 кВт·ч.
Отв. q= 14,9 МДж/(кВт·ч); b = 0,498 кг/(кВт·ч).
148. Паровая турбина мощностью N = 25 МВт работает при начальных параметрах p1 = 3,5 МПа и t1 == 400 °С. Конечное давление пара р2 = 0,004 МПа.
Определить часовой расход топлива при полной нагрузке паровой турбины, если к.п.д. котельной установки ηку = 0,82, теплота сгорания топлива Qнр = 41870 кДж/кг, а температура питательной воды tпв = 88 °С. Считать, что турбина работает по циклу Ренкина.
Отв. В = 6430 кг/ч.
149. Турбины высокого давления мощностью N = 100000 кВт работают на паре при р1 = 9 МПа и t1 = 480 °С, р2 = 0,004 МПа. Определить термический к.п.д. цикла Ренкина для данных параметров, и достигнутое улучшение термического к.п.д. по сравнению с циклом Ренкина для параметров пара: p1 = 2,9 МПа, t1 = 400 °С; р2 = 0,004 МПа.
Отв. ηt = 42,1 %; ε = 14,4%.
150. Паротурбинная установка мощностью N = 200 МВт работает по циклу Ренкина при начальных параметрах р1 = 13 МПа и t1 = 565 °С. При давлении р' = 2 МПа осуществляется промежуточный перегрев пара до первоначальной температуры. Давление в конденсаторе р2 = 0,004 МПа. Температура питательной воды tпв = 160 °С.
Определить часовой расход топлива, если теплота сгорания топлива Qнр = 29,3 мДж/кг, а к.п.д. котельной установки ηку = 0,92.
Отв. В = 49 624 кг/ч.
