Также может быть проведена оценка показателя надежности программы.
Пример расчета надежности программного средства (методика)
Работоспособным называется такое состояние ПИ, при котором оно способно выполнять заданные функции с параметрами, установленными требованиями ТЗ. С переходом ПИ в неработоспособное состояние связано состояние отказа.
Причины отказа ПИ и технической системы различны. ПИ не свойственен физический износ, а моральное старение, которому в большей степени подвержены программы, не может привести к отказу ПИ.
Причиной отказа ПИ является невозможность его полной проверки в процессе тестирования и испытаний. При эксплуатации ПИ в реальных условиях может возникнуть такая комбинация входных данных, которая вызывает отказ. Таким образом, работоспособность ПИ зависит от входной информации, и чем меньше эта зависимость, тем выше уровень надежности. Кроме того, причинами отказов ПИ могут быть ошибки, вызванные внутренними свойствами ПИ или реакцией программы на изменение внешней среды функционирования. Это значит, что даже при самом тщательном тестировании, если предположить, что удалось избавиться от всех внутренних ошибок, никогда нельзя с уверенностью утверждать, что в процессе эксплуатации ПИ отказ не возникнет.
Классификация программных ошибок по категориям основана на эмпирических данных, полученных при разработке различных ПИ. Под категорией ошибок понимается видовое описание ошибок конкретных типов. В полной классификации выделено более 160 типов категорий, объединенных в 20 классов.
Основным средством определения количественных показателей надежности являются модели надежности, под которыми понимают математическую модель, построенную для оценки зависимости надежности от заранее известных или оцененных в ходе создания ПО параметров.
Все модели надежности объединяются в два класса: аналитические и эмпирические.
Аналитические модели бывают: динамические и статические. В динамических моделях поведение программного средства (появление отказов) рассматривается во времени.
В статических – появление отказа не связывают со временем, а учитывают только количество ошибок от числа тестовых прогонов (по области ошибок) или зависимость количества ошибок от характеристики входных данных (по области данных).
Эмпирические – модели сложности и модели, определяющие время доводки программы.
Аналитическая модель Шумана.
Исходные данные для модели Шумана, которая относится к динамическим моделям дискретного времени, собираются в процессе тестирования программного изделия в течение фиксированных или случайных временных интервалов. Каждый интервал – это стадия, на которой выполняется последовательность тестов и фиксируется некоторое число ошибок.
Модель Шумана может быть использована при определенным образом организованной процедуре тестирования. Использование модели Шумана предполагает, что тестирование проводится в несколько этапов. Каждый этап представляет собой выполнение программы на полном комплексе тестовых данных. Выявленные ошибки регистрируются, но не исправляются. По завершении этапа на основе собранных данных о поведении ПИ на очередном этапе тестирования может быть использована модель Шумана для расчета количественных показателей надежности. После этого исправляются ошибки, обнаруженные на предыдущем этапе, при необходимости корректируются тестовые наборы и проводится новый этап тестирования. При использовании модели Шумана предполагается, что исходное количество ошибок в программе постоянно и в процессе тестирования может уменьшаться по мере того, как ошибки выявляются и исправляются. Новые ошибки при корректировке не вносятся. Скорость обнаружения ошибок пропорциональна числу оставшихся ошибок. Общее число машинных инструкций в рамках одного этапа тестирования постоянно.
Предполагается, что до начала тестирования в ПИ имеется ET ошибок в течение времени t обнаруживается eС ошибок в расчете на команду в машинном языке.
Таким образом, удельное число ошибок на одну машинную команду, оставшихся в системе после t времени тестирования, равно
 ,
,
где IT – общее число машинных команд, которое предполагается постоянным в рамках этапа тестирования.
В модели предполагается, что значение функции частоты отказов Z(t) пропорционально числу ошибок, оставшихся в ПИ после израсходованного на тестирование времени t.
 ,
,
где С – некоторая константа, t – время работы ПИ без отказа.
Тогда, если время работы ПИ без отказа t отсчитывается от точки t=0, а t остается фиксированным, функция надежности или вероятность безотказной работы на интервале времени от 0 до t, равна:
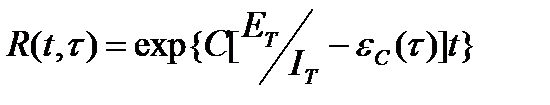 ;
;
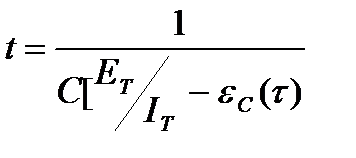 .
.
Из величин, входящих в последние две формулы, не известны начальное значение ошибок в ПИ (ЕТ) и коэффициент пропорциональности – С. Для их определения проводится следующие рассуждения. В процессе тестирования собирается информация о времени и количестве ошибок на каждом прогоне, т.е. общее время тестирования t складывается из времени каждого прогона:
t=t1+t2+t3+ … +tn.
Предполагая, что интенсивность появления ошибок постоянна и равна l, можно вычислить ее как число ошибок в единицу времени
 ,
,
где Ai – количество ошибок на i-м прогоне.

Имея данные для двух различных моментов тестирования tА и tВ, которые выбираются произвольно с учетом требования eС(tВ) > eC(tA), можно сопоставить уравнения для расчета времени при tА и tВ.
 ;
;
 .
.
Вычисляя последние два отношения получим:
 ,
,
 .
.
Теперь можно рассчитать надежность программы.
Пример.
В тестируемой программе 1000 операторов. В процессе последовательных тестовых прогонов получены следующие данные:
| № прогона | 1 | 2 | 3А | 4 | 5 | 6 | 7 | 8 | 9 | 10В |
| Количество ошибок | 5 | 4 | 2 | 5 | 7 | 2 | 3 | 3 | 2 | 3 |
| Время прогона, с | 4 | 4 | 3 | 4 | 6 | 4 | 4 | 5 | 3 | 2 |
Решение. Нужно выбрать две точки (два момента времени) так, чтобы число ошибок, найденных на интервале от А÷В, было больше, чем на интервале от О÷А.
eС(tА) = 11/1000 = 0,011 – ошибка, найденная соответственно на этапе тестирования О÷А;
eС(tВ) = 0,025 – то же на этапе А÷В;
tА =11 – время от начала тестирования до А;
tВ =28 – время на интервале А÷В;
lА = 11/11 = 1 –интенсивность появления ошибок на 1-м интервале;
lВ = 25/28 = 0,89 – интенсивность появления ошибок на 2-м интервале;
 ошибок.
ошибок.
 .
.
Подставляя различные t (время) при t=39, можно рассчитать вероятность безотказной работы в течение соответствующего времени.
Предлагаемая модель может быть модифицирована путем исключения зависимости от числа машинных команд.
Функция частоты отказов в течение i-го интервала тестирования остается постоянной и равной:

Известные параметры ЕТ и С предлагается вычислять исходя из следующих соотношений:
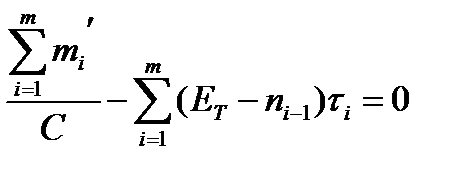 ;
;
 ,
,
где ti – время i-го прогона (время i-го интервала); mi¢ - число прогонов, завершившихся отказом на i-м интервале (число ошибок в i-м интервале); m – общее число тестовых интервалов; ni – общее число ошибок обнаруженных (но не включенных) к i-му интервалу.
Все эти данные можно получить в ходе тестирования. Вычислив значения параметров ЕТ и С можно определить показатели:
1. Число оставшихся ошибок в программе – NT = ET – n;
2. Надежность – R(t) = exp{ - C (ET - n) t }, t ³ 0.
Достоинство этой модели по сравнению с предыдущей заключается в том, что можно исправлять ошибки, внося изменения в текст программы в ходе тестирования, не разбивая процесс тестирования на этапе, чтобы удовлетворить требованию постоянства машинных инструкций.
Статические модели принципиально отличаются от динамических прежде всего тем, что в них не учитывается время появления ошибок и не используется ни каких предположений о поведении функции риска l(t). Эти модели строятся на твердом статистическом фундаменте.
Простая интуитивная модель.
Использование этой модели предполагает проведение тестирования двумя группами программистов независимо друг от друга, использующими независимые тестовые наборы. В процессе тестирования каждая из групп фиксирует все найденные ею ошибки. При оценке числа оставшихся в программе ошибок результаты тестирования обеих групп собираются и сравниваются.
Получается, что первая группа обнаружила N1 ошибок, вторая – N2, а N12 – это ошибки, обнаруженные обеими группами.
Если обозначить через N неизвестное количество ошибок, присутствовавших в программе до начала тестирования, то можно эффективность тестирования каждой из групп определить как

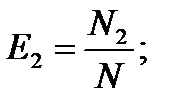
Предполагая, что возможность обнаружения всех ошибок одинакова для обеих групп, можно допустить, что, если первая группа обнаружила определенное количество ошибок, она могла определить то же количество любого случайным образом выделенного подмножества. В частности, можно допустить, что
 .
.
Из формулы N2=E N, подставив в последнее выражение получим:
 или
или  .
.
Значение N12 известно, а E1 и Е2 можно определить как N12/N1 и N12/N2. далее предполагая, что обе группы, проводящие тестирование, имеют равную вероятность обнаружения общих ошибок, ее можно рассчитать последующей формуле:
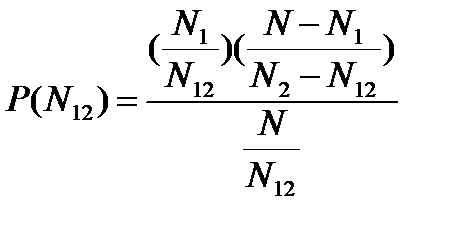 ,
,
где P(N12) – вероятность обнаружения N12 «общих» ошибок тестирования программы независимыми группами.
Модель Коркорэна.
В соответствии с данной моделью оценивается вероятность безотказного выполнения программы на момент оценки.
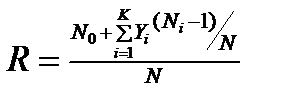 ,
,
где N0 – число безотказных выполнений программы; N – общее число прогонов; К – априори известное число типов;  ai – вероятность выявления при тестировании ошибки i-го типа.
ai – вероятность выявления при тестировании ошибки i-го типа.
В этой модели вероятность ai должна оцениваться на основании априорной информации или данных предшествующего периода функционирования однотипных программных средств. Наиболее часто встречающиеся ошибки и вероятности их выявлений при тестировании ПИ прикладного назначения приведены в таблице.
| № п/п | Тип ошибки | Вероятность появления ошибки |
| 1 | Ошибки вычислений | 0,09 |
| 2 | Логические ошибки | 0,26 |
| 3 | Ошибки ввода-вывода | 0,16 |
| 4 | Ошибки манипулирования данными | 0,18 |
| 5 | Ошибки сопряжения | 0,17 |
| 6 | Ошибки определения данных | 0,08 |
| 7 | Ошибки в БД | 0,06 |
Учебно-методическое издание
Н.А. Соловьев, Д.В. Горбачев
ИНФОРМАЦИОННЫЕ СИСТЕМЫ И ТЕХНОЛОГИИ
Методические рекомендации






