1. Вычислить:
а)  ; б)
; б) 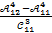 ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и) 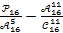 ; к)
; к)  ; л)
; л)  ; м)
; м)  ;
;
с)  ; т)
; т)  ; у)
; у)  ; ф)
; ф)  .
.
2. Сколько разных четырехзначных чисел можно записать, используя девять значащих цифр, при условии, что ни одна цифра не повторяется?
3.Сколько можно провести разных плоскостей через 8
точек пространства, при условии, что никакие четыре из них не лежат в одной плоскости?
4. Сколько существует способов выбора 3 карандашей из
коробки, в которой содержится 12 карандашей разного цвета, при условии, чтобы ни один из них не был черным?
5. Сколько четырехзначных чисел, которые делятся на 5,
можно составить из цифр 0; 1; 3; 5; 7,при условии, что ни одна цифра в числе не повторяется?
6. Сколькими способами можно группу из 15 учащихся
разделить на две группы так, чтобы в одной группе было 4 человека, а в другой – 11 человек?
7. Найти все натуральные  , которые удовлетворяют
, которые удовлетворяют
неравенству:
а)  ; б)
; б)  ;
;
в) 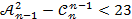 ; г)
; г)  .
.
Решение уравнений, в которых неизвестная величина находится в составе комбинаторных формул. Решение таких уравнений целесообразно проводить по такому алгоритму:
v Найти область определения уравнения. Рассмотрим,
v какие ограничения накладываются на  и
и  в основных комбинаторных формулах Найти область определения уравнения.
в основных комбинаторных формулах Найти область определения уравнения.
Рассмотрим, какие ограничения накладываются на  и
и  в основных комбинаторных формулах
в основных комбинаторных формулах

| 

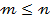
|  множество, состоящее из натуральных чисел и числа 0. множество, состоящее из натуральных чисел и числа 0.

| |

| 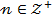
| 0 
| |

| 

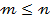
| 
|
v Заменить формулы соответствующими
Произведениями и выполнить тождественные преобразования там, где это возможно
v Решить полученное алгебраическое уравнение и
Проверить принадлежность найденных корней области определения
v Выполнить проверку
8. Решить уравнения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  .
.
9. Найдите все натуральные  , которые удовлетворяют условию:
, которые удовлетворяют условию:
а)  ; б)
; б)  ;
;
в)  =
=  ; г)
; г)  .
.
Решение комбинаторных задач
Комбинаторные задачи бывают разных видов. Но большинство из них решают, применяя два основных правила: правило суммы и правило произведения.





Если элемент  можно Если элемент
можно Если элемент  можно
можно
выбрать  способами, выбрать
способами, выбрать  способами,
способами,
а элемент 
 спосо- а элемент
спосо- а элемент 
 спосо-
спосо-
бамии, то выбор  или бамии, то выбор
или бамии, то выбор  и
и 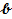
 можно осуществить (пары
можно осуществить (пары 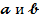 ) можно
) можно
( 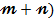 способами. осуществить (
способами. осуществить ( )
)
способами.
Решить задачи
10. Фирма по изготовлению дамских шляп «Камелия» начала выпуск трех новых моделей, для которых был закуплен фетр четырех расцветок. Сколько видов разных шляп может изготовить фирма «Камелия»?
11. На биржу фирма должна отправить двух брокеров, трех
дилеров, одного менеджера. Сколькими способами это можно сделать, если в состав фирмы входят 15 брокеров, 10 дилеров, 5 менеджеров?
12. Из колоды карт, которая содержит 52 игральных
карты(из них 4 туза), взяли 10 карт. В скольких случаях среди них будет хотя бы один туз?
13. Три гимнастки Украины принимали участие в
Олимпийских соревнованиях в Пекине вместе с другими 33 спортсменками других стран. Сколько существует способов распределения призовых мест, среди участниц команды Украины, при условии, что ни одно место не может быть разделено?
14. В чемпионате Украины по футболу принимают участие
18 команд. Сколько существует способов распределения призовых мест, если известно, что команды «Днепр», «Динамо», «Шахтер», «Черноморец» и «Таврия» займут первые пять
мест?
15. Каждая буква азбуки Морзе – это последовательность точек и тире. Сколько разных букв можно составить, если использовать для каждой из них: а) 5 символов; б) не более 5 символов?
16. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько разных номеров можно составить, используя 30 букв и 10 цифр.
17. Для полета в космос необходимо укомплектовать экипаж, который состоит из командира корабля, первого и второго помощников, двух бортинженеров и одного врача. Тройка руководителей полета набирается из 25 летчиков, бортинженеры – из 20 специалистов, а врач – из 8 медиков. Сколькими способами ( ) можно укомплектовать экипаж? В ответ запишите
) можно укомплектовать экипаж? В ответ запишите  : 106 и округлите до единиц.
: 106 и округлите до единиц.






