Основные тождества:
- 
;
- 
;
- 
;
- 
;
- 
;
- 
;
- 
;
- 
.
К основным законам алгебры логики, действующим при сложении и умножении переменных относятся:
- переместительный закон - 
или 
;
- сочетательный закон - 
или 
;
- распределительный закон 
или 
;
- закон поглощения - 
или 
;
- закон склеивания - 
или 
;
- закон отрицания (закон инверсии, теорема Моргана) - 
или 
.
Теорему Моргана для сложных логических выражений можно сформулировать следующим образом:
- инверсия любого сложного выражения, в котором аргументы (либо их инверсии) связаны операциями дизъюнкция и конъюнкция может быть представлена тем же выражением с изменением всех знаков конъюнкции на знаки дизъюнкции, знаков дизъюнкции на знаки конъюнкции и инверсией всех аргументов.
Элементарные логические функции характеризуются дополнительно пятью свойствами.
1. Свойство сохранения нуля. Функция обладает этим свойством, если на нулевом наборе аргументов значение функции равно нулю.
.
Свойством сохранения нуля обладают функции: f0 , f1 , f2 , f3 , f4 , f5 , f6 , f7 .
2. Свойство сохранения единицы. Функция обладает этим свойством, если на единичном наборе аргументов значение функции равно единице.
.
Свойством сохранения единицы обладают функции: f1 , f3 , f5 , f7 , f9 , f11 , f13 , f15.
3. Свойство самодвойственности. Функция обладает этим свойством, если на инверсных наборах аргументов значения функции инверсно.
.
Инверсные наборы аргументов: X1 =0, X2 =0 и X1 =1, X2 =1 или X1 =0, X2 =1 и X1 =1, X2 =0.
Свойством самодвойственности обладают функции: f3 , f5 , f10 , f12.
4. Свойство монотонности. Функция обладает этим свойством, если на неубывающих наборах аргументов, значения функции не убывают.
Необходимо, чтобы при переходе к любому следующему набору, значения функции не убывали.
Свойством монотонности обладают функции: f0 , f1 , f3 , f5 , f7 , f15 .
5. Свойство линейности. Функция обладает этим свойством, если ее можно представить в виде:
Чтобы проверить свойство линейности логической функции, необходимо, используя выражение на наборе аргументов X1 =0, X2 =0 определить а0 , на наборе аргументов X1 =0, X2 =1 определить а2 , на наборе аргументов X1 =1, X2 =0 определить а1 , а затем полученные значения а0 , а1 , а2 подставить в выражение на наборе аргументов X1 =1, X2 =1, если в результате получается верное равенство, то функция линейная. Проверим свойство линейности функции f(x1 ,x2 )= Х1 
Х2.
Результаты вычислений представлены в таблице 2.1.4
Таблица 2.1.4. Проверка свойства линейности.
| Х1 | Х2 | Х1 Х2
| 
| |
| 0 = | 
| а0 =0 | ||
| 1 = |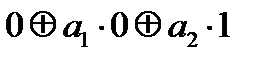 
| а2 =1 | ||
| 1 = | 
| а1 =1 | ||
| 0 = | 
| |||
| 0 = |
Функция линейная.
Свойством линейности обладают функции: f0 , f3 , f5 , f6 , f9 , f10 , f12 , f15.
