«Программное обеспечение по моделированию»
Задание: Составить реферат о программной обеспечении двух-и трехмерному моделированию, применимых при моделированию деталей машин. Студент может предложить свой вариант ПО (аналогичный).
Варианты программных обеспечений:
1. Autocad – двух- и трехмерная система автоматизированного проектирования и черчения;
2. Adams – программное обеспечение для виртуального моделирования машин, механизмов и изделий в сборе;
3. Компас – система трехмерного моделирования;
4. FreeCAD–мультиплатформенное приложение для работы с трехмерными объектами;
5. Rhinoceros 3D – программное обеспечение для трехмерного NURBS– моделирования.
Как написать реферат:
1. Четко сформулируйте тему реферата, которая бы кратко выразила его суть.
2. Подумайте, какие вопросы, и в какой последовательности вам необходимо раскрыть в процессе работы. Это поможет составить план реферата.
3. Изучите литературу по данной теме.
4. Читая выбранные вами книги и статьи, обратите внимание на ссылки авторов на источники, так как они могут заинтересовать вас уже в ходе детального знакомства с темой.
5. Выписки делайте на особых листах, карточках, удобных для последующей обработки и систематизации материала.
6. Классифицируйте выписки, сделанные при чтении литературы, в соответствии с пунктами плана.
7. Реферат пишется по следующему плану:
- во введении объясните, чем вы руководствовались, выбирая данную тему, покажите ее важность и актуальность;
- раскрывая содержание темы, пишите логично, последовательно, высказывания авторов не забывайте взять в кавычки, над которыми обязательно поставьте порядковый номер цитаты, а в примечании сделайте сноски: укажите фамилию, инициалы автора, полное название произведения, место, издательство и год издания, соответствующую страницу;
- в заключении сформулируйте основные выводы, к которым вы пришли. Постарайтесь обосновать, что дала вам работа над данной темой;
- в конце приложите список литературы, которую вы использовали.
8. Оформление должно соответствовать требованиям:
- Объем 20 стр.;
- Междустрочный интервал 1,5;
- Между абзацами 0;
- Шрифт Times New Roman 14;
- Выравнивание по ширине;
- Цвет текста черный, способ записи машинописный, на одной стороне листе;
- Нумерация арабскими цифрами внизу страницы по середине;
- Ссылки на источники указывать порядковым номером по списку источников.
Самостоятельная работа студента №4
Способы записи алгоритмов
Задание: Составить конспект на тему «Способы записи алгоритмов». В конспекте раскройте следующие способы записи алгоритмов:
1. на естественном языке (словесная форма);
2. в виде блок-схем (графическая форма);
3. на языке программирования (Pascal, C, VisualBasic и др.).
В каждой форме записи алгоритмов приведите не менее 3-х примеров записи.
Как составить конспект:
1. Запишите название произведения и его выходные данные.
2. Дайте краткую характеристику исторических условий появления произведения.
3. Составьте план произведения, пункты которого могут последовательно располагаться в тексте конспекта или же на его полях.
4. Запись ведите, как правило, своими словами.
5. Это способствует лучшему осмыслению текста.
6. Применяйте систему подчеркивания, выделяйте большими буквами наиболее важное, используйте условные обозначения и сокращения.
7. Оставляйте в конспекте широкие поля для дополнений, различных заметок, записи незнакомых имен и терминов, требующих разъяснения.
8. При составлении конспекта по нескольким источникам разложите источники после первичного их чтения по широте охвата изучаемой теоретической проблемы, составьте на левой стороне разворота тетради конспект по произведению, принятому за основу, а на правой запишите дополнения из других источников.
9. На полях конспекта делайте для себя краткие выводы, обращения к явлениям современной жизни.
10. Соблюдайте правило цитирования: цитату брать в кавычки, указывая в скобках источник и страницу
Программирование
Задание: Составить программу по каждому разделу. Задания разделены по следующим разделам:
1. Линейные уравнения (linear);
2. Графические уравнения (tree);
3. Массивы (array);
4. Циклы (cycle).
Всего 25 вариантов. Использовать язык программирования Pascalили VisualBasic.
I. Linear
Вариант 1
Определить удельный вес (U) зерновых (%) в площади пашни (S) по формуле:
 ,
где Z – площадь под зерновыми, га
|
| Вариант 2 Определить затраты на производство мяса (З) по формуле: З = Д + К + А + П, где Д – заработная плата, руб. К – затраты на корм, руб.; А – амортизация, руб. П – прочие затраты, руб. |
| Вариант 3 Определить среднемесячное количество работников за 1-й квартал года. Известно количество работников за январь, февраль и март. |
| Вариант 4 Вычислить урожайность ячменя по данной производственной функции: У = 2429,48 – 1,35N + 2,02Р + 4,22К, где У – урожайность, кг/га; N – доза внесения азота, кг д. в./га; Р – доза внесения фосфора, кг д. в./га; К – доза внесения калия, кг д. в. /га. |
| Вариант 5 Рассчитать вес сена (скирда плоская) по формуле: В = (П · 0,56 - Ш · 0,55) · Ш · Д · К, где В – вес сена, ц; П – перекидка, м; Ш – ширина, м; Д – длина, м; К – вес 1 куб. м, ц. |
Вариант 6
Рассчитать вес сена (скирда островерхая) по формуле:
где В – вес сена, ц;
П – перекидка, м;
Ш – ширина, м;
Д – длина, м;
К – вес 1 куб. м, ц.
|
| Вариант 7 Вычислить натуральный вес зерна ячменя (У) по формуле: У = 646,086 – 79.159N + 4,784Р + 32,922К + 0,104Н, где N – норма внесения азота, кг д. в./га; Р – норма внесения фосфора, кг д. в./га; К – норма внесения калия, кг д. в. /га; Н – норма внесения органических удобрений, т/га. |
| Вариант 8 Вычислить себестоимость молока по формуле: С = 3 + К + А + Р + П, где С – себестоимость 1 ц, руб.; 3 – зарплата в расчете на 1 ц, руб.; К – затраты на корм в расчете на 1 ц, руб.; А – амортизация в расчете на 1 ц, руб.; Р – затраты на ремонт в расчете на 1 ц, руб.; П – прочие затраты в расчете на 1 ц, руб. |
| Вариант 9 Вычислить массу 1000 зерен ячменя в г (У) по формуле: У = 44,131 – 3,428N + 1,459P + 2,911K + 0,035H, где N – норма внесения азота, кг д. в./га; Р – норма внесения фосфора, кг д. в./га; К – норма внесения калия, кг д. в./га; Н – норма внесения органических удобрений, т/га. |
Вариант 10
Определить долю пашни (%) в общей земельной площади по формуле:
 ,
где Р – площадь пашни, га;
У – общая площадь, га.
|
| Вариант 11 Рассчитать урожайность озимой пшеницы по данной производственной функции: Y = 1574,09 + 14,72N – 15,31P + 10,24К, где Y – урожайность, кг/га; N – норма внесения азота, кг д. в./га; Р – норма внесения фосфора, кг д. в./га; К – норма внесения калия, кг д. в./га. |
| Вариант 12 Рассчитать вес сена по формуле: В = (П · 0,52 – Ш · 0,46) · Ш · Д · К, где В – вес сена, ц; П – перекидка, м; Ш – ширина, м; Д – длина, м; К – вес 1 куб. м, ц. |
Вариант 13
Рассчитать вес сена (стог низкий) по формуле:
 ,
где В – вес сена, ц;
С – окружность, м;
П – перекидка, м;
К – вес 1 куб. м, ц.
|
| Вариант 14 Вычислить прибыль по формуле: П =Т – С, где П – прибыль, руб.; Т – стоимость товарной продукции, руб.; С – себестоимость товарной продукции, руб. |
Вариант 15
Определить рентабельность производства по формуле:
 ,
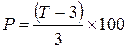где Р – рентабельность, %;
Т – стоимость товарной продукции, руб.;
3 – затраты на товарную продукцию, руб.
|
| Вариант 16 Рассчитать содержание кормовых единиц (Y) по данной производственной функции: Y = 1,2К+ 0,5S + 0,3L + 0,2U + 0,3G + 0,14V, где К – вес комбикорма, кг; S – вес сена, кг; L – вес соломы, кг; U – вес силоса, кг; G – вес сенажа, кг; V – вес кормовой свеклы, кг. |
Вариант 17
Определить среднюю норму внесения удобрений на 1 га пашни (U) по формуле:
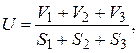где S1, S2, S3 – площади 1, 2, 3 полей (га);
V1, V2, V3 – количество удобрений, внесенное на каждое поле (ц).
|
| Вариант 18 Вычислить содержание сырого протеина в зерне (ц) по формуле: У = 9,438 + 4,759N + 1,163Р – 0,620К + 0,03Н, где N – норма внесения азота, кг д. в./га; Р – норма внесения фосфора, кг д. в./га; К – норма внесения калия, кг д. в./га; Н – норма внесения органических удобрений, т/га. |
| Вариант 19 Определить страховой фонд кормов, ц (S) и общий запас кормов, ц (Z) по формулам: S = P · D; Z=P+S, где Р – потребность в кормах, ц; D – доля страхового фонда, %. |
Вариант 20
Определить среднюю цену продажи зерна (С) по двум каналам реализации (государству и оптовой закупочной фирме):
где V1, V2 – объемы продаж, ц;
К1, К2 – вырученные средства, тыс. руб.
|
| Вариант 21 Определить среднюю зарплату одного работника (СЗР) при заданном фонде (ФЗП) и численности работников (ЧР). |
Вариант 22
Определить сумму вклада через t лет Кt (ден. ед.)по формуле
где К0– первоначальная сумма вклада(ден. ед.)
Е – ставка процента (в долях)
t- период времени
|
| Вариант 23 Рассчитать урожайность ячменя по данной производственной функции: У = 2429,48 – 1,35 · N - 2.02 · P + 4,22 · К, где У – урожайность, кг/га; N, P, K – дозы внесения удобрений: азота, фосфора, калия, кг действующего вещества. |
| Вариант 24 Определить остаток зерна на конец года (К), если известен остаток на начало года (Н), поступление зерна (П) и его расход (Р) за год. Единица измерения – тонна. |
| Вариант 25 Определить сумму отчислений (СО) в государственные фонды от фонда заработной платы предприятия (ФЗП) в соответствии с долей отчислений (Д). Единица измерения сумм – тыс. руб. |
II. Tree
Вариант 1
Составить программу проверки возможности построения параллелограмма из отрезков a, b, c, d.
Вариант 2
Составить программу проверки принадлежности точки М (X, Y, Z) внутренней области шара. X0, Y0, Z0 – координаты центра шара, R – радиус шара.
Вариант 3
Дано три отрезка a, b, c. Составить программу определения, могут ли они являться сторонами прямоугольного треугольника.
Вариант 4
Известны величины 2-х углов. Составить программу проверки возможности построения параллелограмма сданным углами.
Вариант 5
Дано три отрезка a, b, c. Составить программу определения, могут ли они являться сторонами равностороннего треугольника.
Вариант 6
Дано три отрезка a, b, c. Составить программу определения, могут ли они являться сторонами равнобедренного треугольника.
Вариант 7
Дано три значения – А, В, С. Составить программу определения наибольшего из них.
Вариант 8
Дано: R - радиус окружности, а1, а2, а3, а4, а5, а6 - отрезки прямой. Составить программу проверки возможности построения их этих отрезков вписанного в окружность правильного шестиугольника.
Вариант 9
Дано четыре отрезка a, b, c, d. Составить программу определения, могут ли они являться сторонами квадрата.
Вариант 10
Дано: S – площадь круга, С – длина окружности. Составить программу определения, построены ли эти геометрические фигуры на основе радиуса одной длины.
Вариант 11
Пусть в некоторой системе координат заданы своими координатами точка М и вершины A, B, C, D некоторого прямоугольника. Составить программу проверки, принадлежит ли точка М внутренней области прямоугольника.
Вариант 12
Известны величины 4-х углов. Составить программу проверки возможности построения квадрата с этими углами.
Вариант 13
Известны 4-е величины. Составить программу проверки возможности построения прямоугольника со сторонами заданных величин.
Вариант 14
Составить программу проверки возможности построения треугольника по данным о длинах его сторон.
Вариант 15
Известны величины 4-х углов. Составить программу проверки возможности построения четырехугольника с этими углами.
Вариант 16
Составить программу нахождения минимальной величины из 3-х заданных (без использования цикла).
Вариант 17
Составить программу нахождения максимальной величины из трех заданных (без использования цикла).
Вариант 18
Даны 2-е величины: площадь прямоугольника и периметр прямоугольника. Составить программу определения, соответствуют ли эти величины одной геометрической фигуре.
Вариант 19
Дано: S – площадь квадрата, R1 – радиус 1-й окружности, R2 – радиус 2-й окружности. Составить программу определения, можно ли разместить эти окружности внутри квадрата.
Вариант 20
Даны координаты 2-х точек. Составить программу определения, в одном ли квадранте размещены точки.
Вариант 21
Составить программу проверки принадлежности точки А (X, Y) внутренней области окружности. X0, Y0 – координаты центра окружности, R – радиус.
Вариант 22
Известны координаты начала и конца двух отрезков. Составить программу, дающую заключение: пересекаются ли отрезки.
Вариант 23
Известны координаты центра 2-х окружностей и длины их радиусов. Составить программу, дающую заключение: пересекаются ли окружности.
Вариант 24
Известны координаты центра 2-х окружностей и длины их радиусов. Составить программу, дающую заключение: входит ли одна окружность в другую.
Вариант 25
Известны координаты вершин 2-х прямоугольников. Составить программу, дающую заключение: размещается ли один прямоугольник в другом.
III. Array
Вариант 1
Дан числовой массив X(n). Расположить его элементы в порядке возрастания.
Вариант 2
Дан массив X(n). Найти минимальный и максимальный элементы и их координаты.
Вариант 3
Дано 2 одномерных массива. Вычислить новый одномерный массив, как произведение соответствующих элементов исходных массивов.
Вариант 4
Даны массивы X(n) и Y(n). Вычислить 
.
Вариант 5
Дан массив X(n). Умножить каждый элемент массива, равный вводимой величине А на вводимую величину В. Вывести преобразованный массив.
Вариант 6
Дан массив X(n). Преобразовать элементы массива по следующему правилу: если все Xi≤0, то элементы возвести во 2-ю степень, если нет, то каждый второй элемент умножить на 0,1.
Вариант 7
Дано: 2 одномерных массива A(m) и B(m). Вычислить новый одномерный массив C(m), элементы которого вычисляются по формуле:
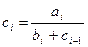
для i > 1, при этом с1 = 0.
Вариант 8
Значения компонент массива А(n) расположены в порядке возрастания. Составить программу, которая меняет массив А, исключая из него компоненту с номером q и вставляя на нужное место новую компоненту со значением d так, чтобы значения измененного массива А также оказались в порядке возрастания. Вывести массив А до и после преобразования.
Вариант 9
Составить программу для перестановки элементов массива X(m) так, чтобы в начале оказались все четные числа, а в конце – нечетные.
Вариант 10
Значения компонент массивов А(n) и B(m) расположены в неубывающем порядке. Составить программу слияния массивов A и B в один массив С(n+m), значения компонент которого также не убывают. Вывести массивы А, В, С.
Вариант 11
Составить программу, определяющую количество и координаты точек, заданных соответствующими компонентами массивов X(n) и Y(n), находящихся в пределах ±D относительно некоторой прямой. Уравнение прямой
Y = AX + B
Вариант 12
Даны массивы X(n) и Y(n). Методом наименьших квадратов определить коэффициенты А и В в линейной зависимости Y=A+BX по формулам
Вариант 13
Дано 2 одномерных массива. Вычислить новый одномерный массив, как разность соответствующих элементов исходных массивов
Вариант 14
Даны массивы X(n), Y(n)и Z(n).
Вычислить 
.
Вариант 15
Дан массив X(n). Умножить каждый элемент массива, равный вводимой величине А на величину А. Вывести преобразованный массив.
Вариант 16
Дан числовой массив X(n). Расположить его элементы в порядке убывания
Вариант 17
Дано 2 одномерных массива. Вычислить новый одномерный массив, как сумму соответствующих элементов исходных массивов.
Вариант 18
Дан массив X(n). Сложить каждый элемент массива, равный вводимой величине А с вводимой величиной В. Вывести преобразованный массив.
Вариант 19
Дан массив X(n). Преобразовать элементы массива по следующему правилу: если Xi≤0, то элементы возвести во 2-ю степень, если нет, то каждый элемент умножить на 0,1.
Вариант 20
Значения компонент массивов А(n) и B(m) расположены в неубывающем порядке. Составить программу слияния массивов A и B в один массив С(n+m), значения компонент которого расположены в убывающем порядке. Вывести массивы А, В, С.
Вариант 21
Дан массив X(n). Определить, сколько элементов массива удовлетворяют условию X(i)< вводимой величины В. Умножить каждый такой элемент массива на вводимую величину В. Вывести преобразованный массив.
Вариант 22
Даны массивы X(n), Y(n)и Z(n). Объединить их в один с чередованием элементов исходных массивов.
Вариант 23
Дан массив X(n). Исключить элементы массива, равные вводимой величине В. Вывести преобразованный массив.
Вариант 24
Дан массив X(n). Найти и напечатать минимальный и максимальный четные элементы и их координаты.
Вариант 25
Дан массив X(n). Расположить его элементы в обратном порядке. Вывести преобразованный массив.
IV. Cycle
Вариант 1
Напишите фрагмент программы, подсчитывающий сумму только положительных из трех данных чисел.
Вариант 2
Даны три числа. Напишите фрагмент программы, подсчитывающий количество чисел, равных нулю.
Вариант 3
Составьте программу возведения заданного числа в третью степень, используя следующую закономерность:
13 = 1
23 = 3 + 5
З3= 7 + 9 + 11
43= 13 + 15 + 17 + 19
53= 21 + 23 + 25 + 27 + 29
Вариант 4
Составьте программу, которая из трех введенных с клавиатуры чисел возводит в квадрат положительные, а отрицательные оставляет без изменения.
Вариант 5
Дана непустая последовательность натуральных чисел. Вычислите сумму положительных элементов последовательности, порядковые номера которых нечетны.
Вариант 6
От прямоугольника 324 х 141 отрезают квадраты со сторонами 141, пока это возможно. Затем вновь отрезают квадраты со стороной, равной 324 -2 х 141 = 42 и т.д. На какие квадраты и на сколько квадратов будет разрезан прямоугольник?
Вариант 7
Стороны прямоугольника заданы натуральными числами М и N. Составьте программу, которая будет находить, на сколько квадратов, стороны которых выражены натуральными числами, можно разрезать данный прямоугольник, если от него каждый раз отрезается квадрат максимально большой площади.
Вариант 8
Исходное данное - натуральное число q, выражающее площадь. Напишите программу для нахождения всех таких прямоугольников, площадь которых равна q и стороны выражены натуральными числами.
Вариант 9
Составьте программу нахождения произведения двух наибольших из трех введенных с клавиатуры чисел.
Вариант 10
Составьте программу для нахождения всех натуральных решений уравнения n2 + m2= k2 в интервале (1,10)
Примечание. Решения, которые получаются перестановкой n и m, считать совпадающими.
Вариант 11
Найдите все трехзначные числа, удовлетворяющие каждому из условий:
• любые две цифры различны;
• число равно среднему арифметическому всех трехзначных чисел (включая данное), имеющих тот же цифровой состав.
Вариант 12
Найдите натуральное число от 1 до 10000 с максимальной суммой делителей
Вариант 13
Дано натуральное число n. Можно его представить в виде суммы трех квадратов натуральных чисел? Если можно, то:
• укажите тройку х, у, z таких натуральных чисел, что х2 + у2 + z2 = n
• укажите все тройки х, у, z таких натуральных чисел, что х2 + у2 + z2 = n
Вариант 14
Даны натуральные числа n, m. Получите все меньшие n натуральные числа квадрат суммы цифр которых равен m.
Вариант 15
Произведение N первых нечетных чисел равно р. Сколько сомножителей взято?
Вариант 16
Даны натуральные числа n и m. Найдите все пары дружественных чисел, лежащих в диапазоне от n до m.
Вариант 17
Даны натуральные числа a, b (а< b). Получите все простые числа р, удовлетворяющие неравенствам а =< р =< b.
Вариант 18
Два числа называются взаимно простыми, если их наибольший общий делитель равен 1.
Проверьте, являются ли два данных числа взаимно простыми.
Вариант 19
Даны натуральные взаимно простые числа n, р. Найдите m такое, что, во-первых, m <р, во-вторых, произведение чисел m-n при делении на р дает остаток 1.
Вариант 20
Даны натуральные числа m и n. Найдите такие натуральные взаимно простые числа р и q, что p/q = m/n
Вариант 21
Даны натуральные числа N и p. Получите все натуральные числа, меньшие N и взаимно простые с р.
Вариант 22
Числа Фибоначчи - это такая последовательность целых чисел, в которой два первых числа равны 1, а каждое следующее число равно сумме двух предыдущих (Числа Фибоначчи: 1,1,2,3,5,8,...) Числа Фибоначчи (Fn) определяются формулами:F0= F1= 1; Fn=Fn-1+Fn-2 при n = 2, 3,... Составьте программу определения F — 40-е число Фибоначчи
Вариант 23
Составьте программу, проверяющую, является ли заданное натуральное число совершенным
Вариант 24
Составьте программу получения всех совершенных чисел, меньших заданного числа n
Вариант 25
Составьте программу вычисления s - суммы всех чисел Фибоначчи, которые не превосходят 1000
