Вопросы:
1. Сложение
2. Вычитание
3. Умножение
4. Деление
Сложение
Таблицы сложения легко составить, используя Правило Счета.
Сложение в двоичной системе

| Сложение в восьмеричной системе
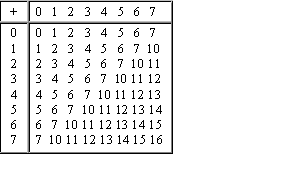
|
Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Примеры.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.


Шестнадцатеричная: F16+616

| Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2. 81 + 5. 80 = 16 + 5 = 21, 1516 = 1. 161 + 5. 160 = 16+5 = 21. |
Пример 2. Сложим числа 15, 7 и 3.


Шестнадцатеричная: F16+716+316
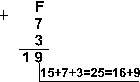
| Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка: 110012 = 24 + 23 + 20 = 16+8+1=25, 318 = 3. 81 + 1. 80 = 24 + 1 = 25, 1916 = 1. 161 + 9. 160 = 16+9 = 25. |
Пример 3. Сложим числа 141,5 и 59,75.




Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25
311,28 = 3. 82 + 181 + 1. 80 + 2. 8-1 = 201,25
C9,416 = 12. 161 + 9. 160 + 4. 16-1 = 201,25
Вычитание
Пример 4. Вычтем единицу из чисел 102, 108 и 1016


Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016.


Пример 6. Вычтем число 59,75 из числа 201,25.

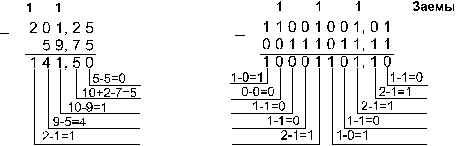
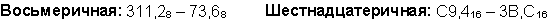

Ответ: 201,2510 - 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2. 82 + 1. 81 + 5. 80 + 4. 8-1 = 141,5;
8D,816 = 8. 161 + D. 160 + 8. 16-1 = 141,5.
Умножение
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение в двоичной системе

| Умножение в восьмеричной системе

|
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример 7. Перемножим числа 5 и 6.


Ответ: 5. 6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21 = 30;
368 = 381 + 680 = 30.
Пример 8. Перемножим числа 115 и 51.


Ответ: 115. 51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865;
133518 = 1. 84 + 3. 83 + 3. 82 + 5. 81 + 1. 80 = 5865.
Деление
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример 9. Разделим число 30 на число 6.


Ответ: 30: 6 = 510 = 1012 = 58.
Пример 10. Разделим число 5865 на число 115.


Восьмеричная: 133518:1638

Ответ: 5865: 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6. 81 + 3. 80 = 51.
Пример 11. Разделим число 35 на число 14.


Восьмеричная: 438: 168
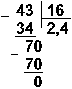
Ответ: 35: 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2. 80 + 4. 8-1 = 2,5.
Упражнения:
1. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
2. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
3. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:
| а) 10111012 и 11101112; | д) 378 и 758; | и) A16 и F16; |
| б) 1011,1012 и 101,0112; | е) 1658 и 378; | к) 1916 и C16; |
| в) 10112, 112 и 111,12; | ж) 7,58 и 14,68; | л) A,B16 и E,F16; |
| г) 10112, 11,12 и 1112; | з) 68, 178 и 78; | м) E16, 916 и F16. |
4. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:

5. Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами):

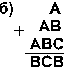

6.Вычтите:
| а) 1112 из 101002; | д) 158 из 208; | и) 1А16 из 3116; |
| б) 10,112 из 100,12; | е) 478 из 1028; | к) F9E16 из 2А3016; |
| в) 111,12 из 100102; | ж) 56,78 из 1018; | л) D,116 из B,9216; |
| г) 100012 из 1110,112; | з) 16,548 из 30,018; | м) ABC16 из 567816. |
7. Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения:
| а) 1011012 и 1012; | д) 378 и 48; |
| б) 1111012 и 11,012; | е) 168 и 78; |
| в) 1011,112 и 101,12; | ж) 7,58 и 1,68; |
| г) 1012 и 1111,0012; | з) 6,258 и 7,128. |
8. Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
9. Разделите 100110101002 на 11002 и затем выполните соответствующее десятичное и восьмеричное деление.
10. Вычислите значения выражений:
а) 2568 + 10110,12 . (608 + 1210) - 1F16;
б) 1AD16 - 1001011002: 10102 + 2178;
в) 101010 + (10616 - 110111012) 128;
г) 10112 . 11002: 148 + (1000002 - 408).
11. Расположите следующие числа в порядке возрастания:
а) 748, 1100102, 7010, 3816;
б) 6E16, 1428, 11010012, 10010;
в) 7778, 1011111112, 2FF16, 50010;
г) 10010, 11000002, 6016, 1418.






