Следствием двух основных теорем теории вероятностей – теоремы сложения и теоремы умножения – являются формула полной вероятности и формула Байеса.
Теорема: Если событие А может произойти при условии появления одного из несовместных событий (гипотез) Н 1, Н 2,…, Нn, образующих полную группу, то вероятность события А равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события А:
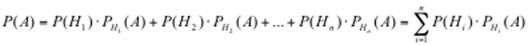
(13)
Формула (13) называется формулой полной вероятности.
Допустим, что произведено испытание, в результате которого появилось событие А. Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
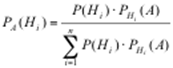
или 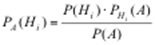
(14)
Формула (14) называется формулой Байеса.
Пример:
На первом заводе на каждые 100 изделий производится в среднем 90 стандартных изделий. На втором заводе на каждые 100 изделий – 95 стандартных и на третьем – 85 стандартных изделий. Продукция этих заводов составляет соответственно 50%, 30% и 20% всех изделий, поставляемых в магазин. Некто зашел в магазин и приобрел стандартное изделие. Найти вероятность того, что это изделие изготовлено на первом заводе.
Решение:
Событие А – приобретено стандартное изделие
Сформулируем гипотезы, при наступлении которых может произойти событие А:
Событие Н 1 –изделие изготовлено на первом заводе
Событие Н 2 –изделие изготовлено на втором заводе
Событие Н 3 –изделие изготовлено на третьем заводе
По условию задачи 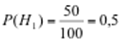
, 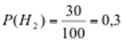
, 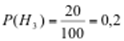
Р (Н 1)+ Р (Н 2)+ Р (Н 3)=1, следовательно, гипотезы образуют полную группу
Для отыскания вероятности того, что приобретенное стандартное изделие изготовлено на первом заводе, воспользуемся формулой Байеса 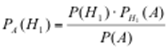
Условные вероятности (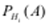
– это вероятность приобретения стандартного изделия, выпущенного i -тым заводом)
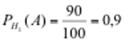
, 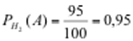
, 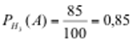
.
По формуле полной вероятности:
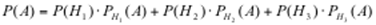
Р (А)=0,5∙0,9+0,3∙0,95+0,2∙0,85=0,905
Тогда искомая вероятность 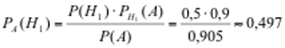
Ответ: 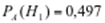
.
Задания для самостоятельной работы
Задача 1. В магазине выставлены для продажи n изделий, среди которых k изделий некачественные. Какова вероятность того, что взятые случайным образом m изделий будут некачественными?
Задача 2. В двух партиях k 1 и k 2 % доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное?
Задача 3. В магазин поступают однотипные изделия с трех заводов, причем i -й завод поставляет mi % изделий (i = 1, 2, 3). Среди изделий i -го завода ni % первосортных. Определить вероятность того, что купленное первосортное изделие выпущено j -м заводом.






