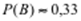РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА И ГОСУДАРСТВЕННОЙ СЛУЖБЫ при ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОРЛОВСКИЙ ФИЛИАЛ
Кафедра Социологии и информационных технологий
Типовой расчет №1
по дисциплине «Теория вероятностей и математическая статистика»
на тему «Основы теории вероятностей»
Орел – 2016.
Цель работы: закрепление теоретических знаний по теме основы теории вероятности, путем решения типовых задач. Усвоение понятий основных видов случайных событий и отработка навыков алгебраических действий над событиями.
Требования к оформлению работы: работа выполняется в рукописном виде, работа должна содержать все необходимые пояснения и выводы, формулы должны содержать расшифровку принятых обозначений, страницы должны быть пронумерованы.
Номер варианта соответствует порядковому номеру студента в списке группы.
Основные теоретические сведения
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений.
Понятие события. Классификация событий.
Одним из основных понятий теории вероятностей является понятие события. Обозначаются события большими латинскими буквами А, В, С,…
Событие – это возможный результат (исход) испытания или опыта.
Под испытанием понимается всякое целенаправленное действие.
Пример: стрелок стреляет по мишени. Выстрел – испытание, попадание в мишень – событие.
Событие называется случайным, если в условиях данного опыта оно может, как произойти так и не произойти.
Пример: Выстрел из ружья – испытание
Соб. А – попадание в цель,
Соб. В – промах – случайные события.
Событие называется достоверным, если в результате испытания оно обязательно должно произойти.
Пример: выпадение не более 6 очков при бросании игральной кости.
Событие называется невозможным, если в условиях данного опыта оно вообще не может произойти.
Пример: выпадение более 6 очков при бросании игральной кости.
События называются несовместными, если наступление одного из них исключает возможность наступления какого-либо другого. В противном случае события называются совместными.
Пример: Брошен игральный кубик. Выпадение 5 очков исключает выпадение 6 очков. Это несовместные события. Получение студентом на экзаменах оценок «хорошо» и «отлично» по двум различным дисциплинам – события совместные.
Два несовместных события, из которых одно должно обязательно произойти, называются противоположными. Событие противоположное событию А обозначают Ā.
Пример: Появление «герба» и появление «решки» при подбрасывании монеты – противоположные события.
Несколько событий в данном опыте называются равновозможными, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие.
Пример: извлечение из колоды карт туза, десятки, дамы – события равновозможные.
Несколько событий образуют полную группу, если в результате испытания обязательно должно произойти одно и только одно из этих событий.
Пример: Выпадение числа очков 1, 2, 3, 4, 5, 6 при бросании игральной кости.
Классическое определение вероятности события. Свойства вероятности
Для практической деятельности важно уметь сравнивать события по степени возможности их наступления.
Вероятностью события называется численная мера степени объективной возможности наступления события.
Назовем элементарным исходом каждый из равновозможных результатов испытания.
Исход называется благоприятствующим (благоприятным) событию А, если его появление влечет за собой наступление события А.
Классическое определение: вероятность события А равна отношению числа благоприятных для данного события исходов к общему числу возможных исходов.
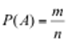
(1)
где P (A) – вероятность события А,
m – число благоприятных исходов,
n – число всех возможных исходов.
Пример: В лотерее 1000 билетов, из них 700 невыигрышных. Какова вероятность выигрыша по одному приобретенному билету.
Решение:
Событие А – приобретен выигрышный билет
Число возможных исходов n =1000 – это общее число билетов в лотерее.
Число исходов, благоприятствующих событию А – это число выигрышных билетов, т.е., m =1000-700=300.
По классическому определению вероятности: 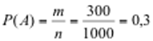
Ответ: 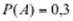
.
Отметим свойства вероятности события:
1) Вероятность любого события заключена между нулем и единицей, т.е. 0≤ P (A)≤1.
2) Вероятность достоверного события равна 1.
3) Вероятность невозможного события равна 0.
Кроме классического существуют еще геометрическое и статистическое определения вероятности.
Элементы комбинаторики.
Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа исходов широко используют формулы комбинаторики.
Пусть дано множество N из n различных элементов.
Определение 1: Комбинации, в каждую из которых входят все n элементов и которые отличаются друг от друга только порядком элементов называются перестановками из n элементов.
P n = n! (2), где n! (n -факториал) – произведение n первых чисел натурального ряда, т.е.
n! = 1∙2∙3∙…∙(n –1)∙ n
Так, например, 5!=1∙2∙3∙4∙5 = 120
Определение 2: Комбинации, каждая из которых содержит m элементов (m ≤ n) и отличающиеся друг от друга или составом элементов или их порядком называются размещениями из n по m элементов.
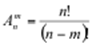
(3)
Определение 3: Комбинации, каждая из которых содержит m элементов (m ≤ n) и отличающиеся друг от друга только составом элементов называются сочетаниями из n по m элементов.
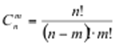
(4)
Замечание: изменение порядка элементов внутри одного сочетания не приводит к новому сочетанию.
Сформулируем два важных правила, часто применяемых при решении комбинаторных задач
Правило суммы: если объект А может быть выбран m способами, а объект В – n способами, то выбор либо А либо В может быть осуществлен m + n способами.
Правило произведения: если объект А может быть выбран m способами, а объект В после каждого такого выбора можно выбрать n способами, то пара объектов А и В в указанном порядке может быть выбрана m ∙ n способами.
Пример: В ящике находятся 6 синих и 8 белых шаров. Наудачу извлекают 3 шара. Найти вероятность того, что: а) выбраны только синие шары, б) выбрано 2 синих и 1 белый шар.
Решение:
а) Событие А – извлечено 3 синих шара.
Для отыскания вероятности события А воспользуемся классическим определением вероятности: 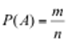
Число возможных исходов n – это число способов извлечения 3 шаров из имеющихся в ящике 14 шаров. Т.к. порядок извлечения шаров не важен, то такие комбинации представляют собой сочетания, т.е. n = 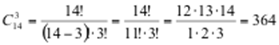
.
Число исходов, благоприятствующих событию А – число комбинаций из имеющихся 6 синих шаров по 3, равно m = 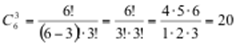
.
Значит, 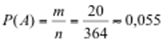
б) Событие В – извлечено 2 синих и один белый шар.
Число возможных исходов n =364
Число исходов, благоприятствующих событию В – число способов выбора из имеющихся 6 синих шаров двух шаров и из 8 белых шаров одного шара, равно
m = 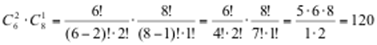
.
Значит, 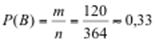
Ответ: а) 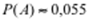
, б)