1. Определители, их свойства. Разложение определителя по элементам строки или столбца.
2. Решение системы линейных уравнений по правилу Крамера.
3. Решение системы линейных уравнений методом Гаусса.
4. Матрицы. Действия над матрицами: сложение, умножение на число, умножение матриц.
5. Векторы. Линейные операции над векторами. Проекция вектора на ось. Координаты векторов.
6. Обратная матрица. Решение систем линейных уравнений в матричном виде.
7. Прямоугольная декартова система координат на плоскости и в пространстве. Полярная система координат.
8. Скалярное произведение векторов, его свойства. Выражение скалярного произведения векторов через координаты перемножаемых векторов.
9. Векторное произведение векторов, его свойства, геометрический смысл, вычисление с помощью координат перемножаемых векторов.
10. Смешанное произведение векторов, его геометрический смысл и вычисление с помощью координат перемножаемых векторов.
11. Прямая на плоскости. Различные формы уравнения прямой на плоскости.
12. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых на плоскости.
13. Эллипс: фокусы, каноническое уравнение, форма. Каноническое уравнение окружности.
14. Каноническое уравнение гиперболы, фокусы гиперболы, асимптоты.
15. Каноническое уравнение параболы, ее фокус и директриса.
16. Плоскость в пространстве. Различные формы уравнения плоскости в пространстве.
17. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
18. Прямая в пространстве. Различные формы уравнений прямой в пространстве.
19. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых в пространстве.
20. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
21. Поверхности 2-го порядка: сфера, эллипсоид, гиперболоиды, параболоиды, конусы, цилиндры. Их канонические уравнения и изображения.
22. Определение функции одной переменной, способы их задания.
23. Основные элементарные функции: y=xn, у=аx, y=logax, y=ln х, y=sin х, y=cos х, y=tg х, y=ctg х,. y=arcsin х, y=arccos х, y=arctg х, y=arcctg х, гиперболические функции.
24. Предел последовательности.
25. Предел функции в точке и в бесконечности.
26. Теоремы о пределах функций одной переменной.
27. Первый замечательный предел.
28. Второй замечательный предел.
29. Понятие бесконечно малой функции. Теоремы о бесконечно малых функциях.
30. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
31. Непрерывность функции. Классификация точек разрыва.
32. Два определения непрерывности функции в точке и на отрезке.
33. Свойства непрерывности функций.
34. Точки разрыва и их классификация.
35. Определение производной функции y=f(x), ее геометрический и механический смыслы.
36. Производные элементарных функций.
37. Теоремы о производной суммы, произведения, частного двух функций.
38. Теорема о связи непрерывности и дифференцируемости функции y=f(x) в точке.
39. Теоремы Ферма, Ролля, Лагранжа, Коши. Их геометрическая интерпретация.
40. Производная функции, заданной параметрически.
41. Производная обратной функции, условия ее существования. Связь производных прямой и обратной функций.
42. Теорема о дифференцировании сложной функции.
43. Производная неявной функции.
44. Производная показательно − степенного выражения у = [u(x)]v(x).
45. Определение дифференциала функции.
46. Применение дифференциала к вычислению приближенного значения функции.
47. Производные и дифференциалы высших порядков.
48. Правило Лопиталя для раскрытия неопределенностей вида 0/0, ∞/∞.
49. Экстремумы функции y=f(x). Необходимое и достаточное условия существования экстремума. Критические точки.
50. Исследование функции на монотонность.
51. Наибольшее и наименьшее значения функции y=f(x) на [а,b].
52. Выпуклость и вогнутость кривой y=f(x). Необходимый и достаточный признаки выпуклости и вогнутости, точки перегиба.
53. Асимптоты кривой.
54. Понятие первообразной и неопределенного интеграла. Основные свойства неопределенного интеграла.
55. Метод замены (подстановки) в неопределенном интеграле.
56. Интегрирование по частям неопределенного интеграла.
57. Вычисление интегралов вида 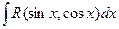 .
.
58. Вычисление интегралов вида 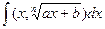 .
.
59. Вычисление интегралов вида 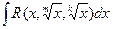 .
.
60. Вычисление интегралов вида 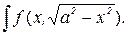
61. Вычисление интегралов вида 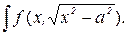
62. Вычисление интегралов вида  .
.
63. Определенный интеграл, его геометрический смысл и основные свойства.
64. Формула Ньютона-Лейбница.
65. Замена переменной в определенном интеграле.
66. Интегрирование определенного интеграла по частям.
67. Вычисление площади плоской фигуры в декартовой системе координат.
68. Вычисление площади плоской фигуры, ограниченной кривой, заданной в параметрическом виде.
69. Вычисление площади плоской фигуры в полярных координатах.
70. Вычисление длины дуги кривой, заданной в декартовой системе координат.
71. Вычисление длины дуги, заданной в полярной системе координат.
72. Вычисление длины дуги кривой, заданной параметрическими уравнениями.
73. Вычисление объема тела вращения.
74. Несобственный интеграл от разрывной функции.
75. Несобственный интеграл с бесконечными пределами интегрирования.
76. Интегрирование рациональных функций.
77. Понятие дифференциального уравнения. Порядок дифференциального уравнения. Интегральная кривая. Общее и частное решение дифференциального уравнения.
78. Задача Коши для дифференциального уравнения 1-го порядка. Формулировка теоремы о существовании и единственности задачи Коши, ее геометрический смысл. Дифференциальное уравнение первого порядка с разделяющимися переменными.
79. Интегрирование однородных дифференциальных уравнений 1-го порядка.
80. Решение линейных дифференциальных уравнений 1-го порядка.
81. Дифференциальные уравнения первого порядка в полных дифференциалах.
82. Интегрирование дифференциального уравнения вида y(n) = f(x).
83. Интегрирование дифференциальных уравнений вида F(x, у',у") = 0.
84. Интегрирование дифференциальных уравнений F(x, у',у") = 0.
________________________________________________________________






