ЗАДАНИЯ
ВсеРоссийской ОЛИМПИАДЫ школьников
ПО АСТРОНОМИИ
Уч. г.
(муниципальный этап)
Класс
- На сколько процентов меняется за сутки скорость наблюдателя, находящегося в Магадане, относительно Солнца вследствие осевого вращения Земли? Широта Магадана - 60 градусов северной широты.
- С какой стороны Земли - с дневной или ночной, энергетически выгодно запускать ракету к Меркурию?
- Оценить скорость расхода топлива (кг/с) в начальный момент запуска космического корабля. Масса корабля 10 тонн, температура сгорания топлива (водород) 1000 К, стартовое ускорение 3g.
- Определите период осевого вращения Солнца, если при наблюдениях в обсерватории солнечное пятно (вблизи центра Солнца на его экваторе) переместилось за 2 суток на 23 мм. Изображение Солнца на экране телескопа имело диаметр 10 см. Угловой радиус Солнца (средний) r =16’.
- Используя карту звездного неба, выполните для каждого рисунка (рис. 1-3) следующие задания:
a) напишите название созвездия, название самой яркой его звезды, ее буквенное обозначение и звездную величину;
б) в какое время года это созвездие лучше всего видно на широте Нижнего Новгорода?
г) какие интересные объекты в нем вы знаете?
| Рис. 1 |
| Рис. 2 |
| Рис. 3 |
- Проснувшись от летаргического сна, вы обнаружили, что находитесь на необитаемом острове, лежащем точно на экваторе. Светит Солнце, на вас – только купальный костюм. Сможете ли вы через час-другой сказать, что сейчас у вас дома в Нижнем Новгороде – зима или лето?
ПРИМЕРНЫЕ РЕШЕНИЯ ЗАДАНИЙ ПО АСТРОНОМИИ
Муниципальный этап 2013
Класс
1. Центр Земли движется по орбите со скоростью 2pR/T, а Магадан относительно центра Земли - со скоростью 2pr/t, где R - расстояние от Земли до Солнца, r - расстояние от Земной оси до Магадана, в точности равное половине радиуса Земли (поскольку широта Магадана - 60°), T - период обращения Земли вокруг Солнца, t - период суточного вращения Земли. Таким образом, скорость Магадана относительно Солнца меняется от 2pR/T-2pr/t до 2pR/T+2pr/t. Их разница по отношению к средней скорости составляет
(4pr/t) / (2pR/T) = 2 r / R × T/t = 6370/149600000 × 365» 1,55%
2. Чтобы ракета перешла на эллиптическую траекторию полета к Меркурию, ее скорость на орбите Земли должна быть меньше круговой. Следовательно, ракету нужно запускать в сторону, противоположную орбитальному движению Земли. Поскольку направления суточного вращения и орбитального обращения у Земли совпадают, при дневном запуске стартовая скорость ракеты складывается со скоростью вращения Земли. Это выгодно. Разница стартовых скоростей дневного и ночного запусков может составить до 1 км/с (поскольку скорость вращения Земли на экваторе 0,5 км/с). Довольно легко доказать, что запуск должен происходить в первой половине дня.
3. Для обеспечения стартового ускорения 3g необходимая сила тяги F должна быть равна 4 Мg, где М - начальная масса ракеты. С другой стороны, эта сила равна реактивной силе, возникающей в результате выброса продуктов сгорания. Пусть m - масса выброшенного газа из ракеты за время t. Тогда F = mv/t = 4Mg, откуда m/t = 4Mg/v. Скорость v - это тепловая скорость атомов водорода при Т =1000 К, поэтому v =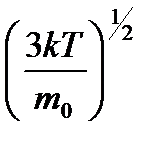 
@ 5Ч103 м/с. Окончательно получаем: m/t ~ 80 кг/с.
4. Смещение пятна за сутки составит r = 11,5 мм. Так как Солнце представляет собой сферическую поверхность, то длина экватора составит L = 2пR = 314 (мм). Следовательно, период осевого вращения Солнца будет S = L/r (суток) = 27,3 суток (без учёта движения Земли вокруг Солнца). С учётом движения Земли получим: 1/S = 1/P - 1/T, где S - продолжительность солнечных суток, P - период вращения Солнца Т - период обращения Земли вокруг Солнца. P = S×T/S+T P = 25,4 суток.
5. 1) Рис.1 – Орион, латинское название Orion, a Ориона (a Ori) – Бетельгейзе, звездная величина 0,42m; Рис.2 – Большая Медведица, латинское название Ursa Major, a Б.Медведицы (a UMa) – Дубхе, звездная величина 1,79 m; Рис.3 – Лебедь, латинское название Cygnus, a Лебедя (a Cyg) – Денеб, звездная величина 1,25 m.
2) Орион наблюдается в вечернее время зимой, Большая Медведица – незаходящее созвездие и наблюдается круглый год, Лебедь – летом и осенью.
3)Для Ориона - Большая туманность Ориона, туманность Конская Голова, кратная система Трапеция.
Для Большой Медведицы - оптически двойная Мицар – Алькор.
Для Лебедя – туманность Северная Америка, двойная Альбирео.
6. Если в северном полушарии зима, то склонение Солнца отрицательно, и при наблюдении с экватора его суточное движение происходит привычным для нас образом – слева направо. В летнее же для европейцев время года склонение Солнца положительно, и суточное перемещение Солнца по небу при наблюдении с экватора происходит справа - налево. Поэтому установить, что в Нижнем Новгороде – зима или лето, особого труда не составит.
Тренировочные задачи с ответами
48. Какую долю земной поверхности может охватить взглядом космонавт с высоты 400 км?
Пусть точка O – центр Земли, K – космонавт и Г – горизонт. Обозначим длины отрезков: ОГ через R и КГ через D. Тогда длина отрезка КО будет равна R + h, где h = 400 км – высота орбиты. Расстояние до горизонта определим из прямоугольного треугольника ГОК по теореме Пифагора: (R + h)2 = D 2 + R 2, откуда D 2 = 2 Rh + h 2 = 2 Rh (1 + h /2 R). Поскольку h << R, второе слагаемое в этой формуле много меньше первого, поэтому им можно пренебречь. В результате получаем формулу для расстояния до горизонта при высоте наблюдателя h << R: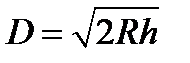 
. Поскольку D << R, площадь поверхности Земли, доступную взгляду космонавта можно вычислить как площадь круга: 
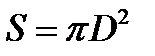, поскольку полная площадь поверхности Земли вычисляется как площадь шара: 
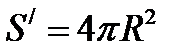. Отношение этих площадей составляет 
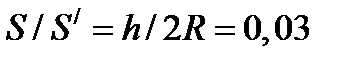(т.е. 3 %).
49. Две звезды имеют одинаковые размеры, но температура поверхности у первой звезды равна 30000 K, а у второй – 5000 K. Какая из этих звезд будет излучать больше энергии в синих лучах? В желтых? В красных?
Первая звезда излучает больше во всех диапазонах спектра. Это зависит только от температуры.
50. Будут ли одинаковы скорость вылета и дальность полета снаряда при выстреле из одной и той же пушки на Земле и на Луне? (сопротивлением земной атмосферы пренебречь)
Кинетическая энергия снаряда зависит только от энергии заряда и соотношения масс пушки (M) и снаряда (m). Если масса пушки велика, то снаряд уносит с собой всю энергию выстрела (E):
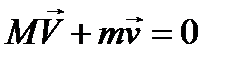– закон сохранения импульса.
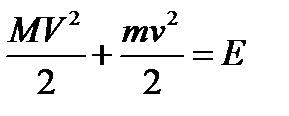– закон сохранения энергии.
откуда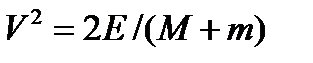 
, поэтому скорость вылета снаряда не зависит от того, на каком небесном теле произведен выстрел. А вот дальность его полета – зависит. Пусть a – угол наклона ствола пушки к горизонту. Тогда дальность полета
.
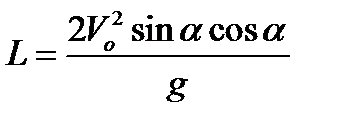Как видим, при одинаковых a и v дальность полета обратно пропорциональна значению g. Например, на Луне та же пушка выстрелит в 6 раз дальше, чем на Земле (а с учетом сопротивления воздуха – еще дальше!)
51. Можно ли увидеть созвездие Южного Креста с территории России? А из северного полушария Земли?
В России – нет, но из северного полушария – да, созвездие полностью видно южнее 27–й параллели.
52. Блеск Солнца равен –26,8 m. Найти блеск полной Луны, считая ее альбедо равным 0,1.
Задачу можно решить без сложных вычислений. Достаточно вспомнить, что видимые угловые диаметры Солнца и Луны практически совпадают, а плотность потока световой энергии, уходящего от Луны, равен 0,1 от плотности потока солнечной энергии на расстоянии Луны (или Земли), или 0,1×(r / R)2 от плотности потока солнечной энергии на поверхности Солнца (r – радиус Солнца, R – расстояние от Солнца до Луны (фактически равно 1.а. е). Подставляя значения и логарифмируя, получаем блеск полной Луны, равный –12,6 m – очень близкое к реальному значению.
53. Наблюдатель фиксирует вид неба регулярно в одно и то же звездное время и постоянно видит Солнце на горизонте. В каком месте Земли и в какое звездное время это может произойти?
Это происходит на северном полярном круге при звездном времени 18 часов или на южном полярном круге при звездном времени 6 часов.
54. Белый карлик имеет массу 0,6 M ã, светимость 0,001 L ã и температуру 2 T ã. Во сколько раз его средняя плотность выше солнечной?
Как известно, светимость пропорциональна R 2 T 4. Плотность, таким образом, пропорциональна M / R 3 или MT 6/ L 3/2. Плотность такого белого карлика в 1,2×106 раз превосходит солнечную.
56. Какова будет примерная форма большой медведицы через 50000 лет и почему?
Из-за прецессии земной оси полюсы мира описывают вокруг полюсов эклиптики малые круги радиусом около 23,5 градусов за период около 26000 лет. Это означает, что через 50000 лет полюс мира будет направлен в ту же точку, что и 2000 лет назад. Это недалеко от звезды альфа в созвездии Дракона. Смена «полярной звезды» не приведет к изменению формы Большой Медведицы: 50000 лет слишком малый срок для того, чтобы стали заметны относительные смещения сильно удаленных звезд.
6. Вычислить, во сколько раз Сириус ярче Полярной звезды.
Принято считать, что при разности в одну звездную величину видимая яркость звезд отличается примерно в 2,5 раза. Тогда разность в 5 звездных величин соответствует различию в яркости ровно в 100 раз. Так, звезды 1-й величины в 100 раз ярче звезд 6-й величины. Следовательно, разность видимых звездных величин двух источников равна единице, когда один из них ярче другого в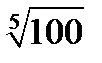 
(эта величина примерно равна 2,512). В общем случае отношение видимой яркости двух звезд I 1: I 2 связано с разностью их видимых звездных величин m1 и m2 простым соотношением
.
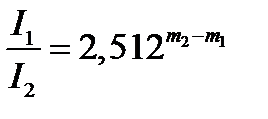Светила, яркость которых превосходит яркость звезд 1 m, имеют нулевые и отрицательные звездные величины (0 m, –1 m и т. д.). Звездные величины Сириуса m 1 и Полярной звезды m 2 находим из таблицы. m 1 = –1,6, а m 2 = 2,1. Прологарифмируем обе части указанного выше соотношения
.
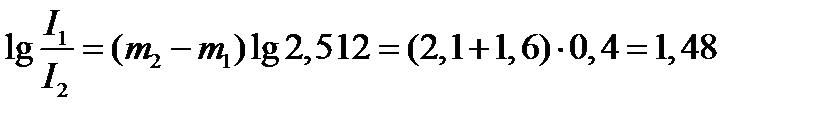Таким образом
.
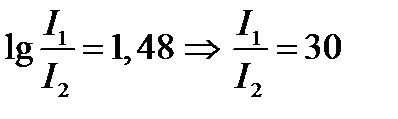Сириус ярче Полярной звезды в 30 раз.
7. Как вы думаете, можно ли долететь на ракете до какого-нибудь созвездия?
Созвездие – это условно определенный участок неба, в пределах которого оказались светила, находящиеся от нас на разных расстояниях. Поэтому выражение «долететь до созвездия» лишено смысла.
5. Какой наибольшей высоты достигает Вега (d = +38о42/) в Бобруйске (j = 53о)?
| Z |
| Z / |
| S |
| N |
| Q |
| Q / |
| P |
| P / |
| j |
| M |
| d |
| h |
| 90o – j |
| j |
| O |
h – высота светила M в верхней кульминации; d – склонение светила; j – широта местности.
Если географическая широта известна, то легко вычислить высоту светила в верхней кульминации:
h = 90o – j + d.
Тогда
h = 90o – 53o +38o42/ = 75o42/.
6. Почему в новолуние Луна с Земли не видна?
Луна в это время находится по туже сторону от Земли, что и Солнце, поэтому к нам обращена темная, не освещенная Солнцем половина лунного шара. В таком положении Земли, Луны и Солнца для жителей Земли может произойти солнечное затмение. Оно бывает не каждое новолуние, так как Луна проходит обычно в новолунии выше или ниже диска Солнца.
3. Определите синодический период обращения Меркурия, зная, что его звездный период обращения вокруг Солнца равен 0,24 года.
Угловая скорость вращения Земли (угол, описываемый ею за сутки) составляет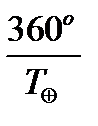 
, угловая скорость Меркурия – 
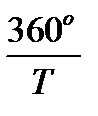, где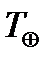 
– число суток в году (сидерический период Земли), T – звездный период обращения планеты, выраженный в сутках. Следовательно, за сутки Земля обгоняет планету на
.
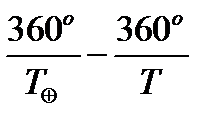Если S – синодический период планеты в сутках, то через S суток Земля обгонит планету на 360о, т. е.
.
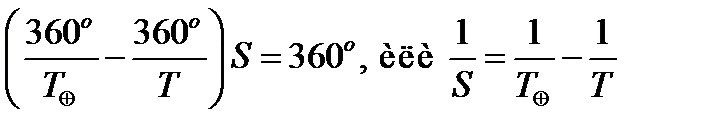Для внутренних планет, обращающихся быстрее, чем Земля,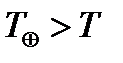 
(планета будет обгонять Землю), надо писать:
.
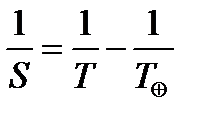Откуда получаем
.
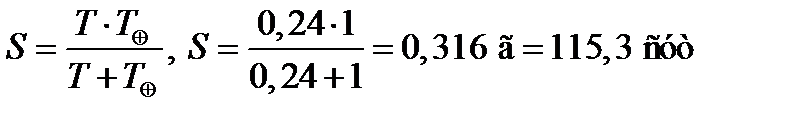4. Вычислите период обращения Нептуна вокруг Солнца, зная, что его среднее расстояние от Солнца равно 30 а. е.
Воспользуемся третьим законом Кеплера:
,
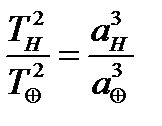где TH – звездный период Нептуна, aH – среднее расстояние от Солнца (большая полуось орбиты), 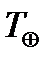– звездный период Земли, 
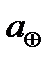– большая полуось земной орбиты (1 а. е.)
Тогда
.
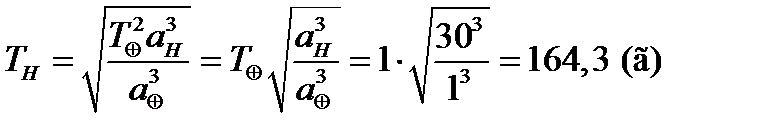5. В спектре звезды желтая линия паров натрия с длиной волны 586 нм смещена на 0,056 нм к красному концу спектра. Определите направление и модуль скорости звезды.
Лучевые скорости (скорости движения небесных светил относительно Земли по лучу зрения) определяются с помощью спектрального анализа. При этом используется эффект Доплера, суть которого состоит в том, что линии в спектре источника, приближающегося к наблюдателю, смещаются к фиолетовому концу спектра, а линии в спектре удаляющегося источника смещены к красному концу спектра.
Эта зависимость выражается формулой
,
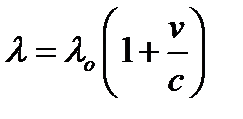где v – лучевая скорость, lо – длина волны, которую принимает наблюдатель от неподвижного источника, l – длина волны, которую наблюдатель принимает от движущегося источника, c – скорость света.
Лучевая скорость равна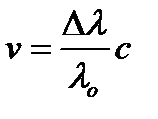 
,
откуда
.
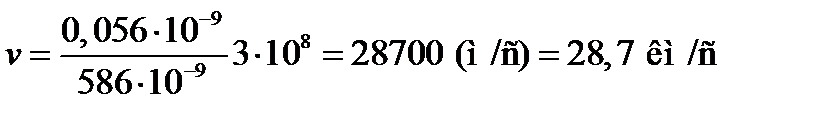6. Вычислите доплеровское смещение линии водорода (lо = 486,13 нм), вызванное приближением звезды вдоль луча зрения со скоростью 40 км/с.
Используя зависимость
,
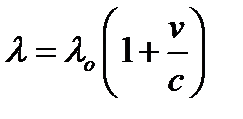находим, что
.
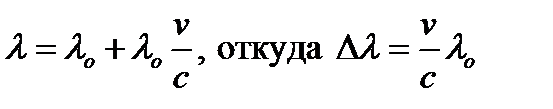Следовательно,
.
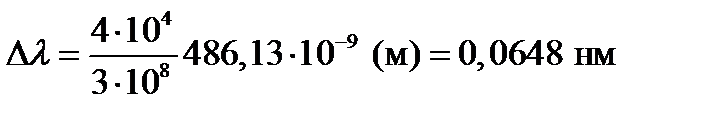Поскольку звезда приближается к наблюдателю, то смещение линии водорода происходит к фиолетовому концу спектра.
4. Масса голубой планеты в 6 раз больше массы Земли. Каков радиус этой планеты, если ускорение свободного падения на ее поверхности такое же, как на Земле.
Как следует из второго закона Ньютона и закона всемирного тяготения,
,
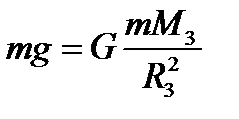m – масса тела, находящегося на поверхности Земли.
Отсюда
.
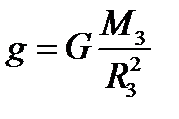Аналогично получаем
,
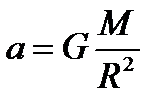здесь a – ускорение свободного падения на планете.
Приравняв выражения для a и g, находим
.
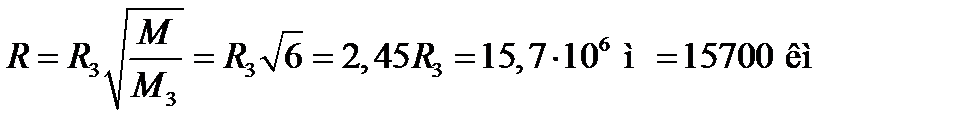Таким образом, радиус планеты равен 15700 км.
5.Во сколько раз надо увеличить скорость вращения Земли вокруг своей оси, чтобы тела на экваторе весили вдвое меньше, чем на полюсе? Считайте, что форма Земли не изменилась бы.
Тела на экваторе участвуют в суточном вращении Земли, при этом их центростремительное ускорение
,
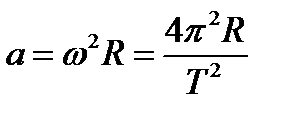направлено к центру Земли и вес тела равен N = m (g – a). Здесь w и T – угловая скорость и период суточного вращения Земли. Согласно условию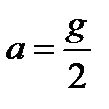 
, откуда 
.
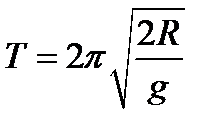Подставив числовые значения, получим T = 2 ч. Таким образом, чтобы тела на экваторе весили вдвое меньше, чем на полюсе, скорость вращения Земли необходимо увеличить в 12 раз.
Заметим, что на самом деле форма столь быстро вращающейся планеты сильно отличалась бы от сферической – планета была бы сильно сплюснута у полюсов.
