Объединение результатов, полученных выше, позволяет решить оптимизационную задачу по поиску наибольшего или наименьшего значения целевой функции среди множества значений х1, х 2, принадлежащих области допустимых решений.
Алгоритм нахождения оптимального решения в задачах линейного программирования с двумя переменными заключается в последовательной реализации следующих этапов.
1. Геометрическое представление области (множества) допустимых решений.
2. Определение направления возрастания (в задаче максимизации) или убывания (в задаче минимизации) целевой функции.
3. Нахождение оптимального решения — точки (точек), в которой (которых) достигается максимум или минимум целевой функции.
Пример 3.2.
Требуется найти такие значения (х1,х2), которые обращают в максимум целевую функцию
Z = 5х1 + x2 
max
и при этом удовлетворяют системе ограничений
3х1 + 2x2 
12,
x1 + 2х2 
4,
2x1 - х2 1,
и условиям неотрицательности
x1 
0, x2 0
Решение
Область допустимых решений, соответствующая данной системе ограничений, была найдена ранее (рис. 3.4). Исследуем поведение целевой функции в этой области и выясним, в какой из точек ОДР целевая функция достигнет наибольшего значения.
Вектор, указывающий направление роста целевой функции Z= 5x1 + х2, имеет координаты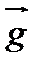 
= {5, 1}. Придадим Z какое-либо значение, например Z = 5. Уравнение линии уровня Z = 5 задает на графике прямую 5x1 + x2 = 5 (рис. 3.8). Очевидно, что чем далее будет перемещаться прямая в направлении 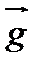, тем большие значения будет принимать Z. Область, в которой возможны перемещения, ограничена синим многоугольником ОДР. Следовательно, наибольшее значение будет достигнуто в крайней точке ОДР. Эта точка — (х1орt,x2opt). Именно в ней и достигается оптимальное решение, при котором Z будет наибольшим из всех возможных. Дальнейшее перемещение линии уровня за пределы ОДР будет приводить к росту Z, однако вне ОДР решения не имеют смысла, т. к. в этих точках будут нарушены ограничивающие условия. Содержательно это означает, что выполнение какой-либо производственной программы (x1, x2), «расположенной» вне области допустимых решений, невозможно из-за отсутствия достаточного для ее реализации запаса ресурсов.
| Z=13 |
| Z=5 |
 -Вектор-градиент
|
| X1 |
| X1+2x2=4 |
| 3x1+2x2=12 |
| 2x1-x2=1 |
Рис.3.8.
| а |
3х1 + 2х2 = 12
2x1 - х2 = 1
Решая ее, находим
x1opt = 2, x2opt =3
Тогда максимальное значение целевой функции будет равно
Zmax =5 x1opt + x2opt = 5 • 2 + 3= 13
Таким образом, оптимальному решению соответствуют следующие значения переменных: xlopt = 2, x2opt = 3. Они обращают целевую функцию в максимум (Zmax = 13) и при этом удовлетворяют системе исходных ограничений.
