В задаче с двумя переменными целевая функция имеет вид
Z=c1x1+ c2x2
Предположим, что Z = 3x1 + x2. Выясним, как графически можно представить целевую функцию в координатной плоскости Х10Х2. Для этого придадим Z какое-либо постоянное значение, например, Z= 3. Тогда получаем
3x1 + x2 =3, или x2 =3-3x1
Это уравнение задает в координатной плоскости Х10Х2 прямую с угловым коэффициентом, равным (-3). Напомним, что угловой коэффициент прямой — это коэффициент, стоящий при аргументе х1, который равен тангенсу угла наклона прямой к оси 0Х1 и, следовательно, задает ее наклон. Нанесем эту прямую на график, представленный на рис. 3.5. Заметим, что для всех точек, принадлежащих данной прямой, значение целевой функции одинаково (постоянно) и равно 3, поскольку все точки прямой удовлетворяют уравнению 3х1 + x2=3.
Положим теперь Z = 5. Тогда в Х10Х2 получаем новую прямую (рис, 3.5), уравнение которой
3x1 + x2 =5, или x2 = 5-3 x1
X2
| X1 |
| Z=5 |
| Z=3 |
Рис.3.5.
Заметим, что угловой коэффициент новой прямой, также как и первой (Z = 3), равен (-3). Следовательно, прямые Z=3и Z=5 параллельны друг другу.
Пусть теперь Z = 6. Рассуждая аналогично, можно построить на графике прямую, задаваемую и этим уравнением. Она также будет параллельна первым двум прямым линиям Z = 3 и Z = 5, поскольку угловой коэффициент и в этом случае остался равным (-3).
Причем по мере удаления от начала координат величина Z возрастает, а при перемещении к началу координат — уменьшается. Легко прийти к выводу: разным значениям целевой функции Z соответствует семейство параллельных прямых.
Для нахождения наибольших и наименьших значений целевой функции необходимо в первую очередь научиться определять, в каком направлении следует перемещать какую-либо линию Z = const, чтобы значение Z возрастало (убывало). Это можно сделать двумя способами. Первый рассмотрен выше: построив пару прямых для разных значений Z и сопоставив их взаимное расположение, определяют направление возрастания или убывания целевой функции. Однако сделать это удобнее на основе использования некоторых сведений из математического анализа, а именно:
• Если задана функция двух переменных Z = f(x1 х2), то линии в Х10Х2 для которых Z = f(x1 х2) = const, называют линиями уровня. Иначе говоря, это те линии, во всех точках которых величина Z постоянна.
• В задачах линейного программирования линиями уровня являются прямые Z = const. Во всех точках, принадлежащих какой-либо линии уровня, значение целевой функции одинаково.
• Важным свойством линий уровня для линейных целевых функций является то, что при их параллельном смещении в одну сторону величина Z только возрастает, а при перемещении в другую сторону — только убывает.
• Определить направление возрастания целевой функции можно с помощью специального вектора, называемого градиентом функции Z = f(x1 х2). Для его обозначения используют символ 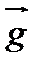 .
.
• Вектор-градиент обладает следующим свойством: в каждой точке он перпендикулярен соответствующей линии уровня и указывает направление ее возрастания.
• В задачах линейного программирования с целевой функцией Z = с1х1 + c2x2 координатами вектора 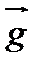 являются его коэффициенты:
являются его коэффициенты: 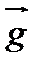 = (с1, c2) (рис. 3.6).
= (с1, c2) (рис. 3.6).
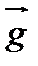 =(с1,с2) =(с1,с2)
|
| C2 |
| X1 |
| Z=const |
| C1 |
Рис.3.6.
Эти утверждения позволяют строить только одну прямую Z = const и далее определять с помощью вектора с координатами 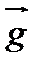 = (c1,c2), в каком направлении целевая функция Z будет возрастать, а в каком убывать.
= (c1,c2), в каком направлении целевая функция Z будет возрастать, а в каком убывать.
Проведенный анализ позволяет сделать следующие выводы.
• Эффективным инструментом для анализа поведения целевой функции являются линии уровня.
• Линии уровня в задачах линейного программирования с двумя переменными — это прямые, во всех точках которых величина Z постоянна.
• Вектор 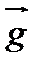 = (с1 ,c2), где с1, с2 — коэффициенты целевой функции, позволяет определить, в какую область значений параметров оптимизации x1 и х2 следует перемещаться, чтобы величина Z возрастала (при ее максимизации) либо убывала (при ее минимизации).
= (с1 ,c2), где с1, с2 — коэффициенты целевой функции, позволяет определить, в какую область значений параметров оптимизации x1 и х2 следует перемещаться, чтобы величина Z возрастала (при ее максимизации) либо убывала (при ее минимизации).
• При изменении коэффициентов (c1, c2) целевой функции Z = с1х1+ c2x2 линии уровня меняют наклон и направление возрастания.






