2.3.1. Основные принципы синтеза по рабочим параметрам
(полиномиального синтеза)
В данном методе синтеза так же, как и при синтезе по характеристическим параметрам, задаются требования к типу проектируемого фильтра, активному сопротивлению нагрузки, ослаблению или коэффициенту передачи мощности в полосе пропускания и задерживания. Однако учитывается, что входное и выходное сопротивления фильтра изменяются в полосе пропускания. В этой связи, фильтр синтезируется в несогласованном режиме, то есть по рабочим параметрам, что в исходных данных отражается требованием 
. Метод основан на обязательном расчете для любых типов фильтров низкочастотного фильтра – прототипа (фильтра нижних частот). В расчетах используется нормирование (
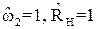) и частотные преобразования.
Эквивалентная схема фильтра разрабатывается не из отдельных одинаковых звеньев, а сразу полностью, обычно в виде схемы цепочной структуры. На рисунке 9 показан вид П-образной цепочной схемы фильтра нижних частот, а на рисунке 10 – вид Т-образной схемы такого же фильтра с ненормированными элементами.
|
|
Основные этапы расчетов, на которых основан данный синтез, следующие:
а) аппроксимация – замена графических требований к коэффициенту передачи мощности аналитическим выражением, например отношением полиномов по степеням 
, что соответствует формулам частотных характеристик реальных реактивных фильтров;
б) переход к операторной форме записи частотных характеристик (замена переменной 
на переменную 
в аналитическом выражении, аппроксимирующем коэффициент передачи мощности);
в) переход к выражению для входного сопротивления фильтра, используя взаимосвязь коэффициента передачи мощности, коэффициента отражения и входного сопротивления фильтра:
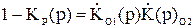, (43)
. (44)
В выражении (44) применяется лишь один коэффициент отражения 
, который соответствует устойчивой электрической цепи (полюса этого коэффициента не имеют положительной действительной части);
г) разложение аналитического выражения для входного сопротивления, полученного из (44), на сумму дробей или в цепную дробь для получения эквивалентной схемы и значений элементов.
Полиномиальный синтез в практических разработках обычно проводится с использованием справочников по фильтрам, в которых выполнены расчеты для данного метода синтеза. В справочниках приведены аппроксимирующие функции, эквивалентные схемы и нормированные элементы фильтров нижних частот. В большинстве случаев в качестве аппроксимирующих функций применяются полиномы Баттерворта и Чебышева.
Ослабление фильтра нижних частот с аппроксимирующей функцией Баттерворта описывается выражением:
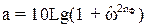, (45)
где 
– порядок фильтра (положительное целое число, численно равное количеству реактивных элементов в эквивалентной схеме фильтра).
Порядок фильтра определяется выражением
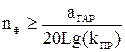. (46)
В таблицах 1, 2 приведены значения нормированных реактивных элементов при аппроксимации Баттерворта, рассчитанные для разных порядков фильтра нижних частот (для схем, аналогичных схемам на рисунках 9, 10).
Таблица 1
Значения нормированных элементов ФНЧ Баттерворта П-образной схемы
| 
| 
| 
| 
| 
| 
| 
|
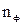
| 1,414 | 1,414 | ||||||
| 0,765 | 1,848 | 1,848 | 0,765 | ||||
| 0,618 | 1,618 | 1,618 | 0,618 | ||||
| 0,518 | 1,414 | 1,932 | 1,932 | 1,414 | 0,518 | ||
| 0,445 | 1,242 | 1,802 | 1,802 | 1,242 | 0,445 |
Таблица 2
Значения нормированных элементов ФНЧ Баттерворта Т-образной схемы
|
| 
| 
| 
| 
| 
| 
| 
|
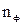
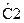
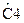
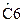
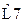
| 1,414 | 1,414 | ||||||
| 0,765 | 1,848 | 1,848 | 0,765 | ||||
| 0,618 | 1,618 | 1,618 | 0,618 | ||||
| 0,518 | 1,414 | 1,932 | 1,932 | 1,414 | 0,518 | ||
| 0,445 | 1,242 | 1,802 | 1,802 | 1,242 | 0,445 |
При синтезе следует учитывать, что для аппроксимации Баттерворта ослабление на границе полосы пропускания обязательно равно 3 дБ.
Ослабление фильтра нижних частот с аппроксимирующей функцией Чебышева описывается выражением
, (47)
где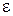 
– коэффициент неравномерности, величина которого зависит от значения неравномерности ослабления в полосе пропускания
. (48)
Для полосы задерживания существуют более простые варианты записи ослабления ФНЧ с аппроксимацией Чебышева, например:
. (49)
По формуле (49) проще определить требуемый порядок фильтра:
. (50)
При аппроксимации Чебышева значения нормированных элементов для электрических схем, показанных на рисунках 9, 10, различаются при разной неравномерности в полосе пропускания, даже при неизменном порядке фильтра. В таблицах 3, 4 приведены рассчитанные нормированные элементы для таких схем ФНЧ, но лишь для одного варианта – для неравномерности в полосе пропускания 
, при 
.
Таблица 3
Значения нормированных элементов ФНЧ Чебышева П-образной схемы
|
|
|
|
|
|
|
|
|
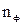
| 0,4668 | |||||||
| 1,3034 | 1,1463 | 1,3034 | |||||
| 1,3824 | 1,3264 | 2,2091 | 1,3264 | 1,3824 | |||
| 1,4468 | 1,3560 | 2,3476 | 1,4689 | 2,3476 | 1,3560 | 1,4468 |
Таблица 4
Значения нормированных элементов ФНЧ Чебышева Т-образной схемы
|
|
|
|
|
|
|
|
|
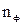
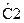
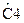
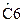
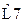
| 0,4668 | |||||||
| 1,3034 | 1,1463 | 1,3034 | |||||
| 1,3824 | 1,3264 | 2,2091 | 1,3264 | 1,3824 | |||
| 1,4468 | 1,3560 | 2,3476 | 1,4689 | 2,3476 | 1,3560 | 1,4468 |
Больше информации можно получить из справочников по синтезу ФНЧ [4], где приводятся не только значения нормированных элементов для разных соотношений сопротивлений внешних цепей, но также коэффициенты и полюса аппроксимирующих полиномов.
2.3.2. Последовательность синтеза ФНЧ по рабочим параметрам
При синтезе по рабочим параметрам, с использованием справочников нормированных реактивных фильтров нижних частот, применяются формулы
(45)–(49) данных методических указаний. Последовательность расчетов для ФНЧ следующая:
а) требования задания к синтезу ФНЧ нормируются, то есть принимается
, 
, 
;
б) определяется порядок фильтра (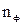) для одного или нескольких видов аппроксимации коэффициента передачи по формулам (46), (50) данных методических указаний. Порядок фильтра в рассматриваемых аппроксимациях равен числу идеальных реактивных элементов в схеме фильтра.
Выбирается Т-образная или П-образная эквивалентная схема, соответствующая рассчитанному порядку. Из справочников нормированных ФНЧ или из таблиц 1–4 п. 2.3.1 данных методических указаний выбираются значения нормированных реактивных элементов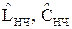 
для рассчитанного порядка фильтра;
в) рассчитываются значения ослабления для нескольких значений нормированных частот в полосе пропускания и в полосе задерживания (без учета тепловых потерь) по формулам (45), (47). Для использования при построении графиков обычных рабочих частот значения нормированных частот необходимо умножать на множитель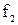 
;
г) элементы эквивалентной схемы ФНЧ денормируются, то есть пересчитываются к требованиям задания:
, (51)
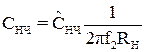; (52)
д) далее проводятся расчеты по пунктам д–ж п. 2.2.2 методики проектирования ФНЧ (ФВЧ) по характеристическим параметрам.
2.3.3. Последовательность синтеза ФВЧ по рабочим параметрам
Для обеспечения возможности синтеза фильтров верхних частот с помощью справочников нормированных ФНЧ применяют следующую методику:
а) нормируются требования задания к синтезу ФВЧ, то есть принимается 
, 
, . С помощью частотного преобразования 
(преобразование ‘ФВЧ – ФНЧ’) требования задания к фильтру верхних частот преобразуются в требования к фильтру нижних частот. При этом 
;
б) проводится синтез эквивалентной схемы ФНЧ с нормированными элементами 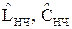по методике пункта б п. 2.3.2;
в) с помощью обратного частотного преобразования ‘ФНЧ – ФВЧ’ схема фильтра нижних частот преобразуется в схему фильтра верхних частот с нормированными элементами 
, причем
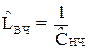, (53)
; (54)
г) рассчитываются значения ослабления для нескольких значений частот в полосе пропускания и в полосе задерживания без учета тепловых потерь для нормированных частот. Для ФВЧ Баттерворта – по формуле
. (55)
Для ФВЧ Чебышева – по формуле
. (56)
Для перехода от нормированных частот к обычным рабочим, как и ранее для ФНЧ, значения нормированных частот необходимо умножить на множитель ;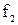
д) элементы эквивалентной схемы ФВЧ денормируются, то есть пересчитываются к требованиям задания:
, (57)
; (58)
е) далее проводятся расчеты по пунктам д–ж п. 2.2.2 методики проектирования ФНЧ (ФВЧ) по характеристическим параметрам.
2.3.4. Последовательность синтеза ПФ (РФ) по рабочим параметрам
При синтезе схем ПФ или РФ по рабочим параметрам так же, как и при синтезе подобных фильтров по характеристическим параметрам, вначале рекомендуется рассчитать эквивалентные схемы фильтров-прототипов для ПФ (фильтра нижних частот) и РФ (фильтра верхних частот). В связи с этим:
а) на первом этапе синтеза, как и в п. 2.2.3, необходимо применить частотное преобразование ПФ – ФНЧ или РФ – ФВЧ, то есть пересчитать заданные требования по ослаблению в требования по ослаблению фильтра-прототипа, используя соотношения между частотами
,
;
б) далее, в зависимости от задания, разрабатывается схема нужного фильтра-прототипа (либо схема ФНЧ по методике п. 2.3.2 (для ПФ), либо схема ФВЧ по методике п. 2.3.3 (для РФ)). Для фильтра-прототипа рассчитываются и строятся графики ослабления и коэффициента передачи по напряжению;
в) для заключительных этапов синтеза ПФ или РФ применяется методика п. 2.2.3, по которой эквивалентные схемы фильтров-прототипов преобразуются в соответствующие эквивалентные схемы полосового или режекторного фильтра. Затем по этой же методике разрабатываются схемы электрические принципиальные ПФ или РФ и пересчитываются графики ослабления и коэффициента передачи по напряжению фильтров-прототипов в графики ПФ или РФ (формулы (41), (42)).
