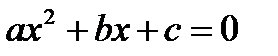(1)
D 
· при D > 0 уравнение (1) имеет два корня: 
, 
(2)
Если а > 0, то вершина расположена ниже оси абсцисс, а ветви параболы направлены вверх, т.е. парабола пересечёт ось в двух точках. Если a < 0, то вершина расположена выше оси абсцисс, и ветви параболы направлены вниз, значит, парабола опять же пересекает ось ОX в двух точках.
· при D = 0 два корня совпадают: 
Вершина параболы у = 
лежит на оси абсцисс, а ветви направлены вверх или вниз в зависимости от знака числа а.
· при D < 0 действительных корней нет, но есть два комплексных корня, которые также вычисляются по формулам (2).
Если а > 0, то ветви параболы направлены вверх, и, следовательно, вся парабола лежит выше оси абсцисс. Если же а < 0, то ветви параболы направлены вниз, и парабола лежит ниже оси абсцисс.
Теорема Виета (если x1, х2 существуют)
Также справедлива формула:
= 
Вершина параболы: 
Наибольшее и наименьшее значение квадратного трёхчлена:
Если a > 0, то квадратный трёхчлен у = 
при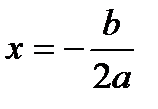 
имеет наименьшее значение, равное 
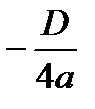(где D 
). Если a < 0, то квадратный трёхчлен имеет при 
наибольшее значение, равное .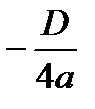
Базовая математика.
Семинар по теме 2.
| Решить уравнение: (х - 1)(х - 2)(х - 3)(х - 4) = 15 | ||
Решить неравенство: 
| ||
Пусть числа x1 и x2 являются корнями квадратного уравнения  . Вычислить, чему равно выражение  .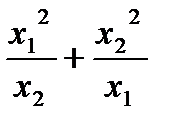
| ||
| Найти значения параметра а, при каждом из которых уравнение 2 х2 + 3 х + а = 0 имеет два различных отрицательных корня. | ||
| Для всех значений параметра а решить неравенство x 2 + ax + 1 > 0 | ||
Найти все значения параметра а, при которых наибольшее значение квадратного трехчлена  на отрезке  не превосходит 2.
| ||
При каких значениях параметра а сумма S квадратов корней уравнения 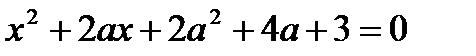 является наибольшей? Чему равна эта сумма?
| ||
При каких значениях параметра а уравнение  имеет единственное решение? Указать эти решения для каждого значения параметра.
| ||
Найти минимальное и максимальное значение параметра а, при которых неравенство  выполняется для всех  .
| ||
| При каких значениях параметра а корни х1, и х2 многочлена 2 х2 – 2(2 а + 1) х + а (а – 1) удовлетворяют неравенствам х1 < а < х2? |
Домашнее задание по теме 2.
Используя теорему Виета, найти сумму квадратов корней уравнения 
| ||
| Найти значения параметра а, при каждом из которых оба корня уравнения х2 – 5 ах + 6 а2 = 0 будут больше 100. | ||
Укажите значение параметра 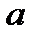 , при котором сумма квадратов всех различных корней уравнения  принимает наименьшее возможное значение.
| ||
Решить для всех значений параметра  :  .
| ||
Для всех значений параметра решить неравенство 
| ||
| При каких значениях параметра а из неравенства х2 – 3 х + 2 < 0 следует неравенство ах2 – (3 а + 1) х + 3 ≥ 0? | ||
| Расположить в порядке возрастания числа 1, 4 и корни уравнения х2 – 2 ах + 2 а2 – 4 а + 3 = 0 | ||
Найти все значения параметра а, при которых все корни уравнения  лежат в отрезке [-1;1]
| ||
Найти все значения параметра а, при которых оба корня уравнения  больше 1
| ||
| При каких значениях параметра а уравнение (а + 4) х2 + 6 х – 1 = 0 имеет единственное решение? |
