Створные наблюдения широко применяют для исследования деформаций сооружений прямолинейной формы (ряда фундаментов или колонн зданий, плотин и т.п.) и определения смещений оползневых пород, то есть когда смещения достаточно знать по одному направлению. При этом координатную систему выбирают так, чтобы с направлением смещений совпадала ось ординат, а с направлением створа – ось абсцисс.
Применяемые в практике высокоточных створных измерений программы можно разделить на простые (программы с необходимым числом измерений) и сложные (программы с избыточным числом независимых измерений). В простых программах нестворность каждой промежуточной точки измеряется относительно одного створа (общего или частного) в прямом и обратном направлениях. В сложных программах нестворности одних и тех же точек определяются независимо от нескольких частных створов в прямом или обратном ходе. Сложные программы, как правило, являются сочетанием нескольких простых программ.
В практике инженерно-геодезических работ при строительстве ряда уникальных сооружений наибольшее распространение получили простые программы створных измерений, основными из которых являются программы общего створа; частей створа; последовательных створов; частных створов [3].
Простейшая из них – программа общего створа (рис.8.8,а), когда нестворности всех точек определяются относительно общего створа между концевыми (опорными) пунктами створа.
Программа общего створа реализуется в двух вариантах:
в створе двух крайних пунктов последовательно определяют нестворности всех промежуточных точек непосредственным (сквозным) визированием;
в створе двух крайних пунктов определяют нестворности промежуточных пунктов, начиная с середины на себя; затем, меняя местами створный прибор и ориентируя визирную цель, также определяют нестворности точек, расположенных во второй части створа; для контроля средняя точка определяется дважды с обоих опорных пунктов створа.
I I΄ II΄ II
Во втором варианте средняя точка определяется с такой же точностью, что и в первом. Нестворности остальных промежуточных точек получаются с более высокой точностью. Однако второй вариант имеет существенный недостаток. Из-за отсутствия обратного хода в нем не исключаются систематические погрешности (инструментальные, личные и т. п.).
По программе частных (пересекающихся) створов (рис.8.8,б) прибор ориентируют относительно всего створа при определении первой промежуточной точки, а нестворности остальных измеряют от створов предыдущей и последующей точек створа: например, частную нестворность второй точки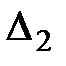 
определяют от створа 1—3, третьей – от створа 2—4 и так далее. В этом случае можно использовать оптический метод визирования по программе равных частных створов. Для измерений по этой программе створ I—II разбивают на равные части и в створе I—2 определяют частную нестворность точки 1. Затем инструмент переносят в точку 1 и в створе 1—3 определяют частную нестворность, 
точки 2 и так далее до створа (п—1)—II. Величина нестворности 
i -й промежуточной точки является функцией измеренных частных нестворностей 
относительно каждого из частных створов, т. е. 
, и может быть получена из следующей системы уравнений:
; 
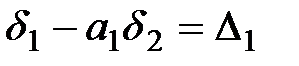где п — число определяемых пунктов створа; i — номер пункта, нестворность которого вычисляется;
Приняв точность измеренных частных нестворностей 
одинаковой, получим формулу для вычисления средней квадратической погрешности определения искомой нестворности
, (8.9)
где k — номер частного створа.
Из изложенного следует, что при одной и той же длине створа погрешность определения средней точки меньше, когда створ разделен на меньшее число частей.
Преимущества программы равных частных створов заключаются в следующем:
она позволяет выполнять измерения даже при неблагоприятных внешних условиях, когда просматривается лишь несколько точек створа;
с большей точностью определяется взаимное положение смежных пунктов, что в ряде случаев является наиболее важным, например, при установке оборудования ускорителей;
практически полностью исключаются погрешности за перефокусировку для средних значений нестворностей, полученных из прямого и обратного ходов.
Программа последовательных створов (рис. 8.8, в). Частную нестворность 
пункта 1 определяют относительно створа I—II, затем относительно частного створа 1 — II измеряют 
и так далее до последнего частного створа (п -1)— II, относительно которого определяют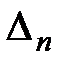 
точки п. Затем аналогично измерения производят в обратном направлении.
. (8.16)
Для повышения точности определения нестворностей бi промежуточных точек по программе последовательных створов необходимо стремиться к уменьшению длины визирного луча независимо от расстояния между конечными пунктами створа. Практически длину визирного луча или шага перестановки прибора можно уменьшать до тех пор, пока суммарное влияние систематических погрешностей на точность створных измерений будет меньше влияния погрешностей визирования. Выбор оптимального шага перестановки инструмента зависит главным образом от заданной точности измерений, конкретной длины и конструкции створа, точности применяемых приборов.
Расчеты показывают, что чем длиннее створ, тем эффективнее применять эту программу при сохранении одной и той же длины шага. Отсюда можно сделать важный практический вывод: чем больше длина створа, тем меньше относительная погрешность 
створных измерений при одной и той же длине шага.
Программа последовательных створов по частям (рис. 8.8, г). В определенных условиях целесообразно применять программу измерений, выгодно сочетающую преимущества программ последовательных створов и равных частных створов.
Пусть створ I—II разбит на три части с узловыми пунктами I’ и II' и промежуточными пунктами 1, 2,... 9. Сущность рассматриваемой программы заключается в следующем:
1) в створе I – II' определяется точка 1, затем в створе 1–II' определяется точка 2, в створе 2—II’ – точка 3;
2)затем в створе I'—II определяется точка 5, в створе 5—II — точка 6 и так далее все точки (7,..., 12), т. е. ориентирование зрительной трубы производится на 2/з общей длины створа;
3) дополнительно определяется нестворность точки I' относительно полного створа I – II.
Приведение узловых точек I' и II' соответственно к створам I—II' и I'—II выполняется по формуле (8.11). Нестворности этих точек относительно общего створа I—II вычисляют по формуле (8.8). Анализ результатов измерений, выполненных по программе последовательных створов по частям, позволяет отметить следующее: чем меньше узловых точек I', II', тем ближе по точности эта программа к программе последовательных створов, и чем больше узловых точек, тем ближе к программе равных частных створов.
Таким образом, приведенный анализ основных программ створных измерений методами оптического визирования позволяет сделать следующие основные выводы:
наиболее точные результаты обеспечивает программа последовательных створов коротким визирным лучом;
если створ разбит на части, то оптимальной является программа последовательных створов по частям, когда в створе минимальное число частей (три части), а все основные и промежуточные точки определяются по программе последовательных створов с ориентированием зрительной трубы на (2/з) L.
Наблюдения створным методом отличаются удобством, простотой, производительностью и достаточной точностью результатов измерений. Этому методу присущи недостатки в том, что смещения определяются только в одном направлении (по оси X), перпендикулярном к створу АВ, а близкое, к наблюдаемым точкам расположение опорных пунктов не дает полной уверенности в их неподвижности, а значит, и надежности результатов измерений.
Наиболее простыми способами измерения нестворностей являются способы подвижной марки, малых (параллактических) углов при неподвижной визирной и измерения угла на контрольном пункте.
Способ подвижной марки.
На определяемых пунктах устанавливается подвижная марка и ее, с помощью микрометренного винта, вводят в створ I-II, заданный оптической линией теодолита, и берут отсчеты по шкале подвижной марки. До начала наблюдений необходимо определить место нуля (МО) подвижной марки. МО является такой отсчет, при котором ось симметрии визирной цели проходит через центр знака. Таких определений необходимо сделать два-три и взять среднее между ними.
Нестворность контрольного пункта вычисляется по формуле
или 
, (8.17)
где 
- средний отсчет по шкале подвижной марки при ее введении в створ.
Ожидаемую погрешность 
определения нестворности пункта подсчитывают по формуле
, (8.18)
где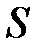 
– расстояние от инструмента до контрольного пункта; 
– погрешности ориентирования створа и фиксирования марки в створе; 
- число приемов определения нестворности; 
- число фиксирований марки в приеме.
Способ подвижной визирной цели следует применять для
непосредственного измерения отклонения деформационной марки
от створа в линейных величинах.
Визирование на подвижную визирную цель, строго центрированную на марке, необходимо осуществлять точными и высокоточными теодолитами, снабженными накладными уровнями.
При использовании в качестве визирной линии луча лазера роль подвижной визирной цели должен осуществлять приемник света с отчетным приспособлением.
Измерения способом подвижной визирной цели следует проводить при двух кругах теодолита в прямом и обратном направлениях, при этом, число приемов должно быть не менее 5. Расхождения между отдельными приемами не должны превышать 1 мм.
Отсчет положения подвижной визирной цели по микрометру теодолита необходимо производить не менее 3 раз, а расхождения в отсчетах не должны превышать 0,3 мм.
Способ малых углов.
теодолит устанавливают на одном опорном пункте, а на втором опорном пункте и на контрольных точках визирные марки.
Измеряют малый угол βi между опорной линией и каждой контролируемой точками. Значения нестворностей вычисляются по формуле:
где 
– расстояние от определяемого пункта до контрольного (определяется с точностью 1:1000).
Для определения отклонения деформационной марки от створа при способе измерения малых (параллактических) углов необходимо провести измерение расстояний от пункта стояния инструмента до марки.
Измерение угла отклонения марки от створа следует проводить точным или высокоточным теодолитами (Tl, T2 и др.), снабженными окулярным или оптическим микрометрами. Малые углы измеряют способом отдельного угла или способом круговых приемов, но используется только оптический микрометр, и сохраняют во всех циклах одну и ту же установку лимба. Половину приемов выполняют при КП, половину – при КЛ.
При измерениях малых углов окулярным микрометром теодолита расхождения не должны превышать:
– между тремя наведениями в полуприемах, а также между значениями одного и того же угла, выведенного из полуприемов – 1,5 деления окулярного микрометра;
– между значениями одного и того же угла из разных приемов в прямом и обратном ходах –1 деление окулярного микрометра.
При измерениях малых углов оптическим микрометром теодолита расхождения не должны превышать:
– между значениями одного и того же угла, выведенного из полуприемов – 3";
– между значениями одного и того же угла из разных приемов в прямом и обратном хода – 1,5".
Среднюю квадратическую погрешность направления из одного приема определяют по формуле Петерса:
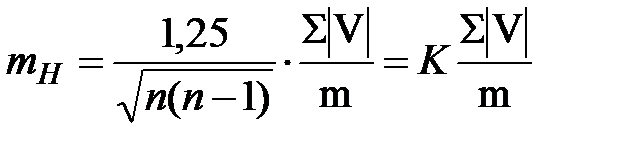(8.20)
Где n – число приемов; m – число направлений; 
– сумма абсолютных значений измеренных направлений от их средних значений, вычисленная по всем направлениям и по всем приемам.Надежность определений зависит от точности измерения малого параллактического угла 
, а расстояние Si может быть измерено нитяным дальномером. При расчете необходимой точности измерения параллактического угланужно учитывать, что ошибка в 1" вызывает ошибку в величине поперечного смещения 0,5 мм на каждые 100 м расстояния.
