РАЗДЕЛ 7. НЕЯВНАЯ ФУНКЦИЯ И ПРИЛОЖЕНИЯ
· Излагается теория неявных функций
· Рассматриваются задачи теории неявных функций, условного экстремума
НЕЯВНАЯ ФУНКЦИЯ. ТЕОРЕМА О СУЩЕСТВОВАНИИ, НЕПРЕРЫВНОСТИ И ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ  , ОПРЕДЕЛЯЕМОЙ УРАВНЕНИЕМ
, ОПРЕДЕЛЯЕМОЙ УРАВНЕНИЕМ 
Термин «неявная функция» относится к способу задания функциональной зависимости между  и
и  и означает, что вместо явной формулы
и означает, что вместо явной формулы  эта зависимость представлена уравнением
эта зависимость представлена уравнением  .
.
Следует отметить, что уравнение  не всегда определяет функцию
не всегда определяет функцию  . Например, уравнение
. Например, уравнение  функцию
функцию  не определяет.
не определяет.
Кроме того, уравнение  не всегда позволяет однозначно выразить
не всегда позволяет однозначно выразить  через
через  . Например, уравнение
. Например, уравнение  , задающее окружность на плоскости, определяет при
, задающее окружность на плоскости, определяет при  две непрерывные функции
две непрерывные функции  и
и  .
.
В этом примере можно например дополнительно потребовать чтобы выполнялось неравенство  . Тогда мы получим только
. Тогда мы получим только  .
.
В общей ситуации условия, при которых существует единственная функция  , задаваемая уравнением
, задаваемая уравнением  дает следующая теорема.
дает следующая теорема.
Теорема. Пусть 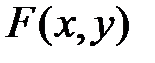 определена и непрерывна вместе с частными производными
определена и непрерывна вместе с частными производными  и
и  в окрестности U точки
в окрестности U точки  такой, что
такой, что  и
и 

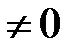 . Тогда существуют числа
. Тогда существуют числа  и
и 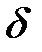 такие, что на множестве
такие, что на множестве  уравнение
уравнение  равносильно уравнению
равносильно уравнению  где
где 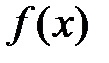 непрерывная и дифференцируемая на
непрерывная и дифференцируемая на  функция, и
функция, и  .
.
Замечание. Равносильность  и
и  означает, что уравнение
означает, что уравнение  однозначно определяет в рассматриваемой области дифференцируемую функцию
однозначно определяет в рассматриваемой области дифференцируемую функцию  такую, что
такую, что  , вообще,
, вообще,  при
при 
 .
.
Теорема. Пусть функция  непрерывна и имеет все непрерывные частные производные в окрестности точки
непрерывна и имеет все непрерывные частные производные в окрестности точки  такой, что
такой, что  , причем
, причем  . Тогда существуют числа
. Тогда существуют числа  такие, что в области
такие, что в области  ,
,  ,
,  уравнение
уравнение  равносильно уравнению
равносильно уравнению  , причем функция
, причем функция  непрерывна и имеет непрерывные частные производные, причем
непрерывна и имеет непрерывные частные производные, причем
 .
.
ФОРМУЛИРОВКА ТЕОРЕМЫ О СУЩЕСТВОВАНИИ, НЕПРЕРЫВНОСТИ И ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ ОПРЕДЕЛЯЕМОЙ УРАВНЕНИЕМ. ФОРМУЛИРОВКА ТЕОРЕМЫ О НЕЯВНЫХ ФУНКЦИЯХ, ОПРЕДЕЛЯЕМЫХ СИСТЕМОЙ УРАВНЕНИЙ
Теорема. Пусть функция  непрерывна и имеет все непрерывные частные производные в окрестности точки
непрерывна и имеет все непрерывные частные производные в окрестности точки  такой, что
такой, что  , причем
, причем  . Тогда существуют числа
. Тогда существуют числа  такие, что в области
такие, что в области  ,
,  ,
,  уравнение
уравнение  равносильно уравнению
равносильно уравнению  , причем функция
, причем функция  непрерывна и имеет непрерывные частные производные, причем
непрерывна и имеет непрерывные частные производные, причем
 .
.
Рассмотрим систему уравнений
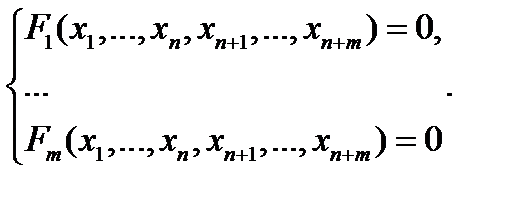
Эта система задаёт совокупность неявных функций. Рассмотрим частный случай такой системы.
Теорема. Пусть  ,
,
где функции  ,
,  ,
,  непрерывны и имеют непрерывные производные в некоторой области
непрерывны и имеют непрерывные производные в некоторой области  (точки
(точки  ). Пусть матрица Якоби
). Пусть матрица Якоби  имеет в этой области ранг 2. Тогда, если, например, минор
имеет в этой области ранг 2. Тогда, если, например, минор  , то в области
, то в области 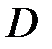 систему можно преобразовать к уравнению
систему можно преобразовать к уравнению
 ,
,  ,
,
где  есть непрерывно дифференцируемая функция от
есть непрерывно дифференцируемая функция от  в области
в области  и
и
 ,
, 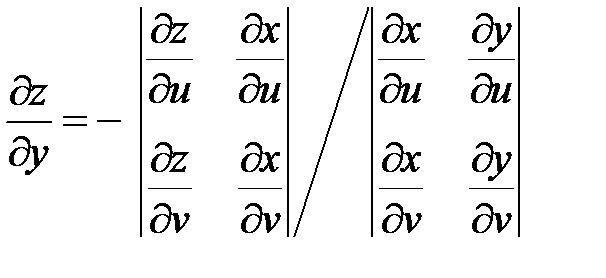 ,
,
Замечание. Уравнения системы определяют в  некоторую поверхность
некоторую поверхность  и называются параметрическими уравнениямиэтой поверхности. Теорема утверждает, что поверхность
и называются параметрическими уравнениямиэтой поверхности. Теорема утверждает, что поверхность  есть график функции
есть график функции  . Обозначают
. Обозначают  ,
,  и уравнения принимают вид
и уравнения принимают вид  .
.
Если зафиксировать  , то
, то 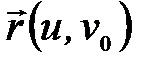 – уравнение координатной линии на
– уравнение координатной линии на  (аналогично,
(аналогично,  при фиксированном
при фиксированном  также представляет собой уравнение координатной линии на
также представляет собой уравнение координатной линии на  ). Векторы
). Векторы 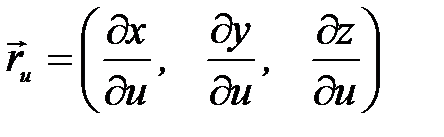 и
и  – касательные векторы к координатным линиям. Если взять точку поверхности, соответствующую параметрам
– касательные векторы к координатным линиям. Если взять точку поверхности, соответствующую параметрам  и рассмотреть касательную плоскость в этой точке, то векторы
и рассмотреть касательную плоскость в этой точке, то векторы  и
и  лежат в этой плоскости. Если ранг матрицы
лежат в этой плоскости. Если ранг матрицы  равен 2, это означает, что
равен 2, это означает, что  и
и  не параллельны и их векторное произведение представляет собой нормальный вектор к касательной плоскости и
не параллельны и их векторное произведение представляет собой нормальный вектор к касательной плоскости и

 ,
,
где буквы  ,
,  ,
,  обозначают соответствующие определители. В этих обозначениях формулы принимают вид
обозначают соответствующие определители. В этих обозначениях формулы принимают вид
 ,
,  ,
,
а единичный вектор  нормали, получаемый при делении вектора на его модуль
нормали, получаемый при делении вектора на его модуль  , равен
, равен
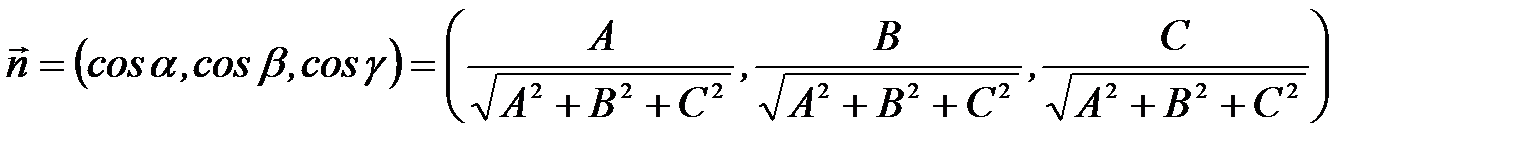
Преобразуем выражение  . По определению векторного произведения,
. По определению векторного произведения, 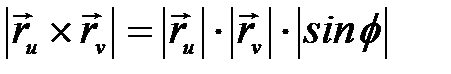 , где
, где  – угол между
– угол между  и
и  . Тогда
. Тогда

 ,
,
где  ,
,  ,
, 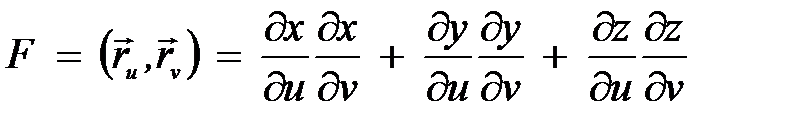 .
.






