Назовём множество выпуклым, еслидля любых двух точек этого множества отрезок, соединяющий их, весь принадлежит этому множеству.
Наглядное определение выпуклости функции можно сформулировать так: функция выпукла вверх(вниз), если она определена на выпуклом множестве и для любых двух точек графика этой функции отрезок, соединяющий их, лежит под(над) графиком этой функции.
Переформулируем это определение в виде, более удобном для проверки и пригодном для функции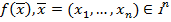 
. Пусть 
, 
, 
, 
). Любую точку 
отрезка, соединяющего точки , можно представить в виде 
, 
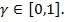Соответствующую ей точку 
графика 
можно представить в виде 
. То, что точка 
лежит над 
, означает, что
()
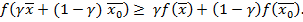Если это неравенство выполнено для всех , 
из некоторого выпуклого множества 
и любого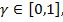 
то мы говорим, что выпукла вверх на 
Выпуклость вниз означает смену неравенства () на противоположный. Если нестрогие неравенства при 
заменяются строгими, то говорят о строгой выпуклости. Легко видеть, что выпуклость вверх функции равносильна выпуклости вниз функции 
, и наоборот.
Если функция имеет непрерывные вторые производные, то условия выпуклости можно представить в удобном для проверки виде.
Теорема. Пусть 
выпуклое подмножество 
. Тогда
-
выпукла вниз тогда и только тогда, когда для любой точки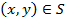 
выполнены неравенства 
. - выпукла вверх тогда и только тогда, когда для любой точки 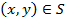выполнены неравенства
. - Если для любой точки 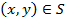выполнены неравенства
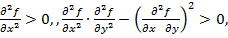то строго выпукла вниз. - Если для любой точки 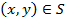выполнены неравенства
то строго выпукла вверх.
В качестве примера применения этой теоремы рассмотрим функцию Кобба-Дугласа
на выпуклом множестве 
= 
.
Так как 
выполнены неравенства 
Кроме того,
По второму пункту теоремы, выпукла вверх. Если 
, то строго выпукла вверх.
Теорема допускает обобщение на функции от большего количества переменных.
Теорема. Пусть 
выпуклое подмножество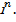 
Рассмотрим матрицу её второго дифференциала (матрицу Гессе)
и её главные угловые миноры
.
Если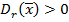 
для всех 
S и всех 
то строго выпукла вниз.
Если 
для всех S и всех то строго выпукла вверх.
Перейдём к случаю нестрогой выпуклости. Назовём главным минором матрицы порядка 
любой её минор, полученный вычеркиванием из исходной матрицы 
строк и столбцов с одинаковыми номерами. Без ограничения общности обозначим 
произвольный главный минор рассматриваемой матрицы.
Теорема. выпукла вниз тогда и только тогда, когда 
для всех S и всех главных миноров порядка 
выпукла вверх тогда и только тогда, когда 
для всех S и всех главных миноров порядка
Результаты этих теорем можно переформулировать в терминах второго дифференциала функции 
Теорема. Пусть выпуклое подмножество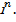
Если 
положительно определённая квадратичная форма, то строго выпукла вниз.
Если 
отрицательно определённая квадратичная форма, то строго выпукла вверх.
выпукла вниз тогда и только тогда, когда 
положительно полуопределённая квадратичная форма.
выпукла вверх тогда и только тогда, когда отрицательно определённая квадратичная форма.
Сформулируем ещё две полезные теоремы.
Теорема. Если 
выпуклы вверх(вниз) и 
то 
выпукла вверх(вниз).
Теорема. Пусть выпуклое подмножество 
, 
определена на интервале, содержащем множество значений 
S. Тогда:
- Если выпукла вверх и
выпукла вверх и возрастает, то 
выпукла вверх. - Если выпукла вниз и выпукла вниз и возрастает, то выпукла вниз.
- Если выпукла вверх и выпукла вниз и убывает, то выпукла вниз.
- Если выпукла вниз и выпукла вверх и убывает, то выпукла вверх.
& Пусть , 
выпуклое подмножество 
. Тогда, в первом случае,
(
) 
( + 
,
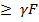что и требовалось доказать. Остальные случаи рассматриваются вполне аналогично.%
Примечание. В этой теореме все условия существенные. Например, если 
,
, то, хотя обе эти функции строго выпуклы вверх, функция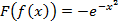 
выпукла вниз в некоторой окрестности точки 
Следовательно, условие возрастания функции в первом утверждении теоремы отбросить нельзя. Условие выпуклости функции тоже нельзя отбросить, как показывает следующий пример. Пусть 
, 
. При этом первая функция выпукла вверх, а вторая возрастает. Однако 
выпуклая вниз функция.
