РАЗДЕЛ 6. ВЫПУКЛОСТЬ
· Излагается важное в дальнейшем понятие выпуклости
· Рассматриваются вопросы выпуклости функций одной и нескольких переменных
ВЫПУКЛОСТЬ НЕПРЕРЫВНОЙ ФУНКЦИИ
Определение. Непрерывная на интервале (a,b) функция f, называется выпуклой вниз (соответственно, выпуклой вверх), если для любых точек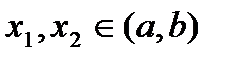 
, 
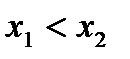, и любого числа 
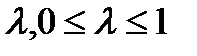справедливо неравенство
(1)
(соответственно, неравенство
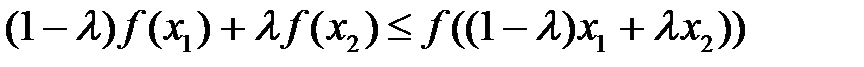. (1’)
В правой части неравенства (1) стоит значение функции f в произвольной точке 
, расположенной на отрезке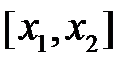 
, содержащемся в интервале (a,b). Левая часть в (1) выражает собой ординату точки координатной плоскости, абсцисса которой равна , 
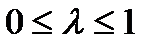, и которая лежит на прямолинейном отрезке (хорде), соединяющем точк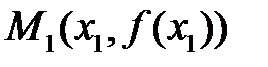и 
и 
графика функции f.
Итак, если непрерывная функция f выпукла вниз на интервале (a,b), то для любых его точек 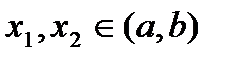, , 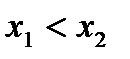график функции f на отрезке 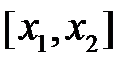расположен ниже хорды, стягивающей концевые точки графика на этом отрезке (см. рис.1, а)).
Рис.1
Аналогично, заключаем, что если непрерывная функция f выпукла вверхна интервале (a,b), то для любых его точек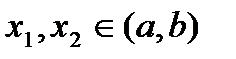 
, 
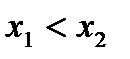, график функции f на отрезке 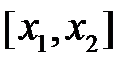расположен выше хорды, стягивающей концевые точки графика на этом отрезке (см. рис.1, b)).
Обозначим 
. Тогда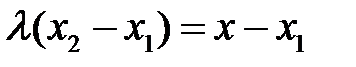 
, откуда 
.
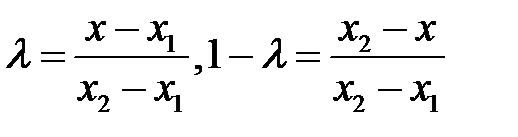Неравенство (1) принимает вид
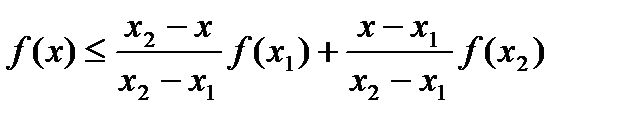, (2)
или, после умножения обеих частей его на множитель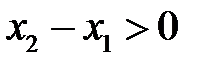 
,
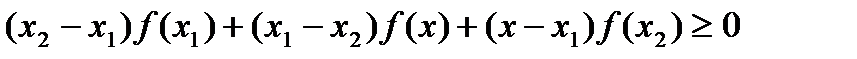. (3)
Поскольку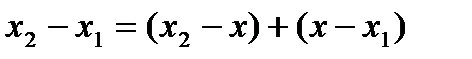 
, то после элементарных преобразований неравенство (4) переходит в неравенство
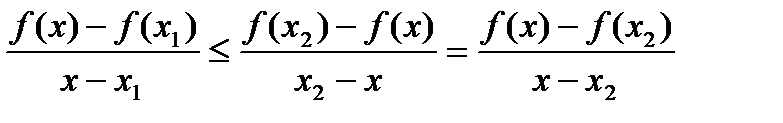, (4)
справедливое для любого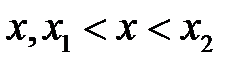 
.
Итак, условие (1) равносильно неравенству (4).
В случае выпуклости вверх знаки неравенств (2)-(4) следует сменить на противоположные.
ВЫПУКЛОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ
Теорема. Для того, чтобы дифференцируемая на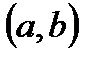 
функция f была выпукла вниз (вверх) на этом интервале, необходимо и достаточно, чтобы её производная функция 
не убывала (не возрастала) на этом интервале.
◄Доказательство проведём для выпуклой вниз функции. Докажем сначала, что её производная не убывает.
Пусть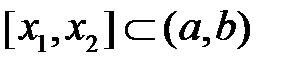 
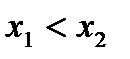, . Переходя в неравенстве (4) к пределу при 
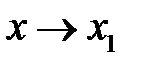, получим:
. (5)
Переходя в неравенстве (4) к пределу при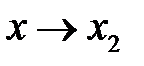 
, получим:
. (6)
Из неравенств (5) и (6) следуют неравенства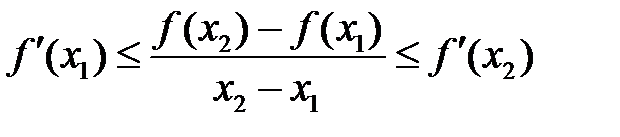 
, что и требовалось доказать.
Обратно, пусть производная функция не убывает на 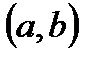. Пусть 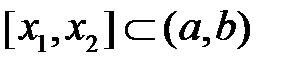, 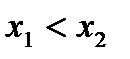. Следует доказать, что выполняется неравенство (4). Для этого заметим, что 
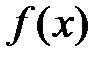дифференцируема на 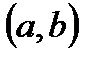, следовательно, непрерывна на 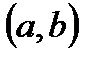и непрерывна на 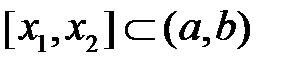. Тогда по теореме Лагранжа, применённой к отрезку 
где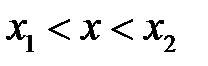 
, находим:
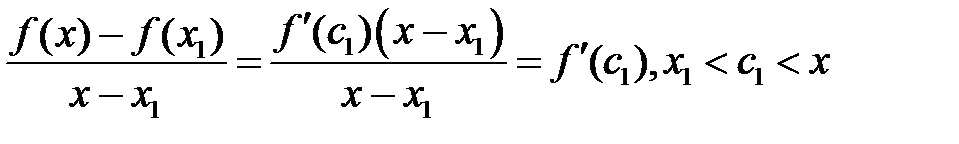. (7)
Аналогично, по теореме Лагранжа, применённой к отрезку 
. 
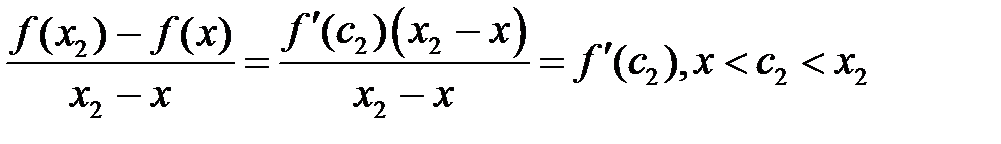. (8)
Так как не убывает на 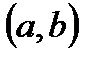, выполняется неравенство 
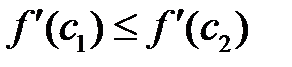, из которого следует, ввиду (7) и (8), неравенство (4), равносильное выпуклости вниз рассматриваемой функции.►
Теорема. Функция 
, дифференцируемая на интервале 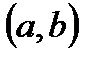,тогда и только тогда выпукла вниз на этом интервале, когда для любой точки 
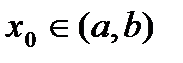и любой точки 
справедливо неравенство
.
Противоположное неравенство
,
справедливо для всех,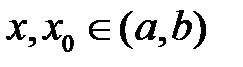 
тогда и только тогда, когда функция выпукла вверх на .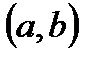
◄ Доказательство проведём для случая выпуклой вниз функции. Пусть сначала дифференцируемая функция выпукла вниз на 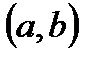. Тогда, какустановлено в теореме 30.1, справедливы неравенства (5) и (6).Неравенство (5) можно преобразовать к равносильному виду
. (9)
Преобразование состоит в умножении обеих частей неравенства (5) на положительный знаменатель и замене обозначений: точку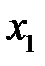 
заменяем на 
, а точку 
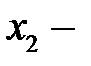на точку 
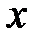, считая, что 
. Точно также, при 
, преобразуем неравенство (6), заменяя точку 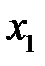на точку 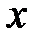, а точку 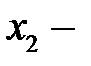на . После этого преобразования снова получим неравенство (9).
Таким образом, если дифференцируемая функция выпукла вниз на интервале 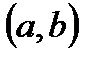, то для всех 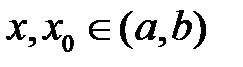выполняется неравенство (9). Для выпуклой вверх функции имеем, соответственно,
.
Обратно, пусть для всех 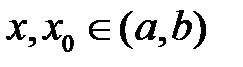выполняется неравенство (9).
Рассмотрим произвольные точки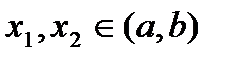 
, 
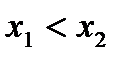. Применяя неравенство (9) к точке 
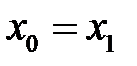и считая 
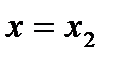, получим неравенство 
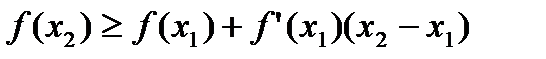, а применяя его к точке 
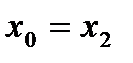и считая 
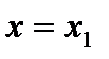, получаем неравенство 
, на основании которых, с учётом условия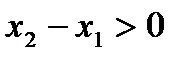 
, имеем
.
Следовательно, производная функции 
не убывает на 
. По теореме 30.1 функция выпукла вниз на . ►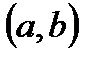
Геометрически свойство выпуклости вниз дифференцируемой функции f на 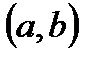означает, что её график в пределах этого интервала располагается выше касательной, проведенной в любой точке графика; для выпуклой вверх дифференцируемой функции картина противоположная (см. рис. 2).
Рис.2
Замечание 1. Если обозначить
,
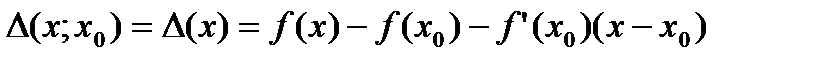то свойство выпуклости вниз(вверх) дифференцируемой функции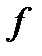 
на 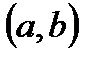равносильно тому, что для любой точки 
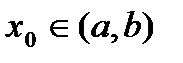неравенство 
(
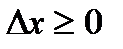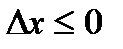) справедливо для всех 
. Отметим, что 
