
Найдем токи:

Задача 3.2

Электрическая цепь, изображенная на левом рисунке, состоит из источника постоянного напряжения Е = 3В, миллиамперметра с очень маленьким внутренним сопротивлением, четырех постоянных и одного переменного резистора. На правом рисунке приведен график зависимости показаний миллиамперметра от величины переменного сопротивления R. Найти величины сопротивлений постоянных резисторов R1 и R2.
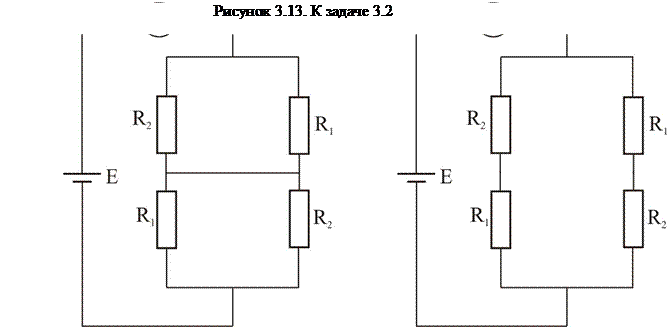
Решение. Заметим, что приведенная зависимость является скорее «устрашающим», чем заметно усложняющим элементом задачи. Для решения нам понадобятся только две точки приведенной зависимости, при R=0 и очень большом R. Пусть сопротивление переменного резистора R=0. Тогда схему можно перерисовать в виде, показанном на рисунке 3.12 слева. Полное сопротивление такой цепи равно r1, а текущий через амперметр ток I1.


Если сопротивление переменного резистора наоборот, очень велико, то схему можно перерисовать как на правом рисунке 3.13.Полное сопротивление такой цепи равно r2, а текущий через амперметр ток I2.


Исключая из полученной системы уравнений, например, величину R2, приходим к квадратному уравнению, позволяющему определить R1.

Откуда

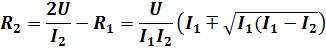
Заметим, что формулы симметричны - выражения для R1 и R2 переходят друг в друга при замене знака перед квадратным корнем. Это связано с тем, что исходная схема соединения резисторов, также симметрична.
Из графика, приведенного в условии на правом рисунке, видно, что I1=1*10-3A, I2 = 0,75*10-3 A. Подставляя эти значения в полученные формулы и выбирая в первой перед корнем знак <+>, а во второй знак <->, получим R1=6 кОм, R2=2 кОм. При противоположном выборе знаков получим: R2=6 кОм, R1=2 кОм.
Задача 3.3
Найти эквивалентное сопротивление изображенной на рисунке 3.14 цепи при условии, что R1=R2=R3=R, а R4= 2R.
 |
Решение. Прежде чем приступим к решению задачи перерисуем её в более удобный вид. Расставим точки равного потенциала. Входную точку назовем точкой A,а выходную точкой В. Отметим, что оба конца резистора R4 имеют один и тот же потенциал А, а значит ток через него не пойдет. Из точки А в точку В можно попасть как через резистор R1, так и через резисторы R2 и R3. В перерисованной схеме они будут соединены параллельно. В итоге цепь будет выглядеть как на рисунке 3.15.
 |
Получившаяся схема представляет собой три параллельно соединенных резистора, а полное сопротивление получившейся цепи равно R/3.
Задачи для самостоятельного решения.
Задача D.3.1(a) Найти полное сопротивление цепи представленной на рисунке 3.16.
 |
Задача D.3.2(a) Найти полное сопротивление цепи представленной на рисунке 3.17.
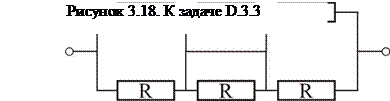 |
Задача D.3.3 (a)Найти полное сопротивление цепи представленной на рисунке 3.18.
 |
Задача D.3.4(b) Найти силу тока, текущего через сопротивление R5(рисунок 3.19), если R1=R2=R3=R4=10 Ом, R5= 3 Ом, U=12 В. Найти также общее сопротивление цепи.
Задача D.3.5 (g)Электрическая цепь состоит из семи последовательно соединенных резисторов: R1=1кОм, R2=2кОм, R3=3кОм, R4=4кОм, R5=5 кОм, R6=6 кОм, R7=7 кОм и четырех перемычек.(рисунок 3.20). Входное напряжение U= 53,2 В. Укажите, в каком из резисторов сила тока минимальна. Найдите эту силу тока. В каком из резисторов сила тока максимальна? Найдите ее.
Задача D.3.6 (g)
 |
В электрических цепях(рисунок 3.21) электрические сопротивления RAB между зажимами A и B и RCD между зажимами C и D равны, а сопротивления R1,R2 и R3 заданы. Найдите все возможные сопротивления Rx и докажите,что других решений нет.
 |
Указание: Можно воспользоваться тем фактом, что для всякой схемы соединенной «треугольником» существует эквивалентная схема «звезда»
Задача D.3.7 (g)В цепи, изображенной на рисунке 3.22 два резистора из трех с неизвестными сопротивлениями R1,R2 и R3 имеют одинаковое сопротивление. Напряжение между точками 2 и 0 равно 6 В, а между точками 3 и 1 равно 10 В. Определите неизвестные сопротивления.

 |
Задача D.3.8 (b)Закрытый непрозрачный ящик содержит внутри электрическую цепь, состоящую лишь из резисторов. От трех точек этой цепи имеются выводы 1,2 и 3 снаружи ящика. Омметр присоединенный к выводам 1 и 2,показывает 3 Ом, присоединенный к выводам 2 и 3 – 5 Ом, к выводам 1 и 3 -6 Ом. Нарисовать, какие цепи с наименьшим возможным числом резисторов могут находиться внутри ящика.
Ответы:
D.3.1 7/5 R
D.3.2 14/23 R
D.3.3 R
D.3.4 I5=0,R=10 Ом
D.3.5 Imax=I4=13.3 мА Imin=I5=2 мА
D.3.6 RX=R1 и RX=R3
D.3.7 R3=R2= 5 Ом R1=2,5 Ом или R3=R1=10 Ом R2=20 Ом






