«Исследование функции и построение графика»
П р и м е р 3.11. Провести исследование функций и построить их графики. а) 
Решение.
Будем проводить исследование в последовательности, которая предлагалась в общей схеме (подразд. 2.2).
I. Элементарные исследования.
1. Область определения функции (подразд. 2.3) 
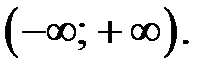
2. Исследуем функцию на четность (нечетность) (подразд. 2.4).
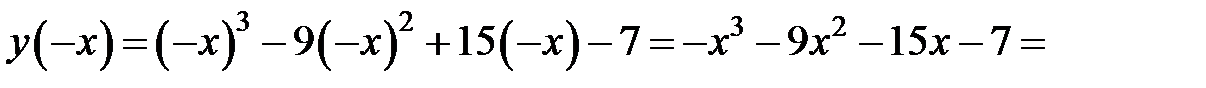


 − следовательно, это функция общего положения.
− следовательно, это функция общего положения.
3. Очевидно, что данная функция не является периодической (подразд. 2.5).
4. Точки пересечения графика функции с осями координат (подразд. 2.6).
При  (нули функции)
(нули функции)  Разложим левую часть уравнения на множители, разделив многочлен
Разложим левую часть уравнения на множители, разделив многочлен  на
на  без остатка (следствие теоремы Безу), где
без остатка (следствие теоремы Безу), где  − корень уравнения, найденный подбором из чисел:
− корень уравнения, найденный подбором из чисел:  (целые делители числа
(целые делители числа  − свободный член многочлена). Уравнение принимает вид:
− свободный член многочлена). Уравнение принимает вид:  тогда
тогда 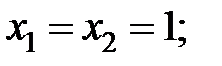
 Таким образом,
Таким образом, 
 − точки пересечения графика функции с осью
− точки пересечения графика функции с осью 
При 

 − точка пересечения графика функции с осью Оу.
− точка пересечения графика функции с осью Оу.
5. Находим интервалы знакопостоянства (подразд. 2.7). Отметим нули функции на оси Ох и найдем знаки функции на каждом из интервалов (рис.1).
| + |
| _ |
| _ |
| х |
| Знак функции |

|

|
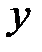
|
| Рис. 1. Интервалы знакопостоянства |
Получаем, что при  график функции лежит ниже оси абсцисс, при
график функции лежит ниже оси абсцисс, при  − выше нее.
− выше нее.
6. Исследуем функцию на непрерывность (подразд. 2.8). Учитывая область определения (см. выше), можно утверждать, что данная элементарная функция является непрерывной на всей числовой оси.
7. Асимптоты графика функции (подразд. 2.9):
а) вертикальных асимптот нет, так как нет точек разрыва 2-го рода;
б) наклонная асимптота: 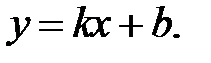



следовательно, наклонных асимптот нет.
На эскиз графика функции нанесем точки пересечения с осями координат 
 ,
, 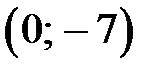 , отметим участки, где график лежит выше и ниже оси Ох.
, отметим участки, где график лежит выше и ниже оси Ох.
II. Исследование функции по первой производной.
Исследуем функцию на монотонность и экстремум (подразд. 2.10).
Находим критические точки 1-го рода:
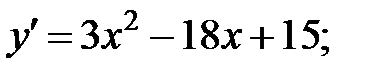

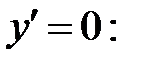


 − критические точки 1-го рода.
− критические точки 1-го рода.
| Знак производной |
| + |
| + |
| _ |
| х |
| Поведение функции |
| max |
| min |

|

|

|

|
| Рис. 2. Интервалы монотонности, точки экстремума |
Из диаграммы на рис. 2 видно: 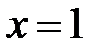 − точка максимума,
− точка максимума,  − точка минимума.
− точка минимума.
Значения функции в точках экстремума: 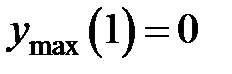 ,
, 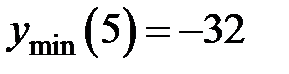 , тогда координаты точки максимума функции:
, тогда координаты точки максимума функции: 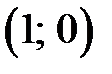 , а координаты точки минимума:
, а координаты точки минимума:  . Интервалы монотонности: при
. Интервалы монотонности: при  − функция возрастает, при
− функция возрастает, при  − убывает.
− убывает.
На эскиз графика функции нанесем точки экстремума 

III. Исследование функции по второй производной.
Исследуем функцию на выпуклость и точки перегиба (подразд. 2.11).
Находим критические точки 2-го рода.



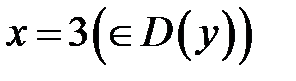 − критическая точка 2-го рода.
− критическая точка 2-го рода.
| + |
| Точка перегиба |
| х |
| Поведение функции |
| Знак второй производной |

|

|
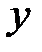
|
| Рис. 3. Интервалы выпуклости, точки перегиба |
| _ |
| О |
| у |
| -32 |
| -7 |
| пер |
| max |
| min |
Рис. 4. График функции
  . .
|

|
| х |
| -16 |
 − точка перегиба. Значение функции в точке перегиба:
− точка перегиба. Значение функции в точке перегиба:  . Координаты точки перегиба графика функции
. Координаты точки перегиба графика функции 
Интервалы выпуклости и вогнутости: при  график функции обращен выпуклостью вверх (выпуклый); при
график функции обращен выпуклостью вверх (выпуклый); при 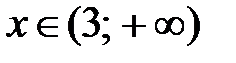 график функции обращен выпуклостью вниз (вогнутый).
график функции обращен выпуклостью вниз (вогнутый).
На эскиз графика функции (рис. 4) нанесем точку перегиба  .
.
IV. Построение графика функции.
На основании проведенного исследования строим график функции (см. рис. 4). Дополнительные точки:  ;
;  .
.
б) 
Решение.
I. Элементарные исследования.
1. Область определения функции 
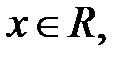 кроме точек
кроме точек 

т. е. 
2. Четность, нечетность функции.

 Следовательно, функция нечетная, график функции будет симметричен относительно начала координат.
Следовательно, функция нечетная, график функции будет симметричен относительно начала координат.
3. Функция непериодическая.
4. Точки пересечения графика с осями координат: при 
 при
при 
 Следовательно,
Следовательно,  − точка пересечения с осями координат
− точка пересечения с осями координат  и
и 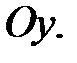
| Знак функции |
| -1 |
| _ |
| + |
| + |
| _ |
| х |

|

|

|

|
| Рис. 5. Интервалы знакопостоянства |
Таким образом, при  − график функции выше оси абсцисс, при
− график функции выше оси абсцисс, при  − ниже нее.
− ниже нее.
6. Исследуем функцию на непрерывность.
В точках 
 функция терпит разрыв (см. подразд. 2.8, теорема 3). Выясним поведение функции вблизи точек разрыва (характер разрыва).
функция терпит разрыв (см. подразд. 2.8, теорема 3). Выясним поведение функции вблизи точек разрыва (характер разрыва).




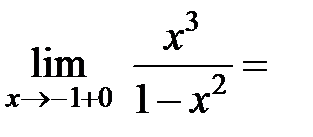



В точке  функция терпит разрыв 2-го рода.
функция терпит разрыв 2-го рода.






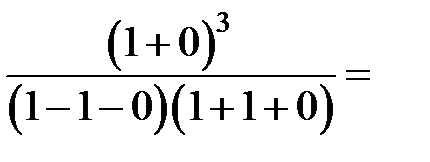

В точке  функция терпит разрыв 2-го рода.
функция терпит разрыв 2-го рода.
7. Найдем асимптоты графика функции.
а) 
 − вертикальные асимптоты, так как в этих точках функция имеет бесконечные разрывы (см. п. 6).
− вертикальные асимптоты, так как в этих точках функция имеет бесконечные разрывы (см. п. 6).
б) Наклонная асимптота: 

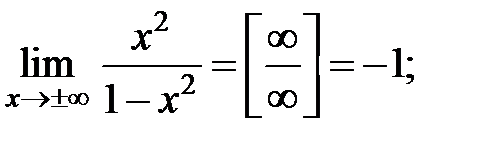
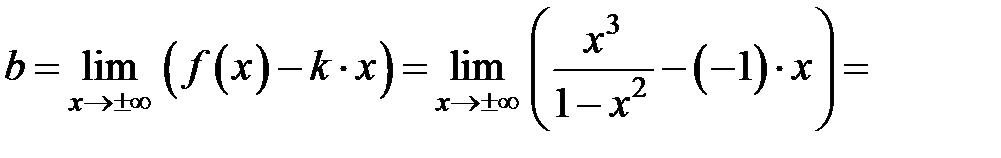
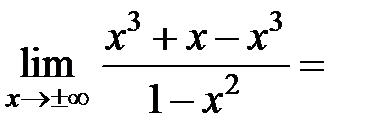
= 
 (Пределы нашли по правилу Лопиталя.)
(Пределы нашли по правилу Лопиталя.)
Следовательно,  − наклонная асимптота.
− наклонная асимптота.
На эскиз графика функции нанесем точку пересечения с осями координат  отметим участки, где график лежит выше и ниже оси Ох, пунктиром проведем асимптоты
отметим участки, где график лежит выше и ниже оси Ох, пунктиром проведем асимптоты 
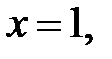
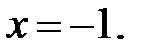
II. Исследование функций по первой производной.
Исследуем функцию на монотонность и экстремум.




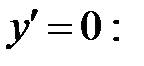
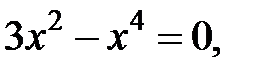
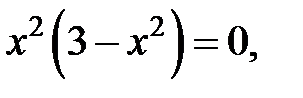

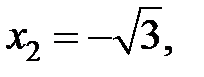

Производная  не существует в точках
не существует в точках  . Следовательно,
. Следовательно, 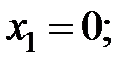


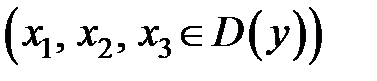 − критические точки 1-го рода. Точки
− критические точки 1-го рода. Точки  не принадлежат
не принадлежат  и поэтому не являются критическими.
и поэтому не являются критическими.
Из диаграммы на рис. 6 видно:  − точка минимума,
− точка минимума, 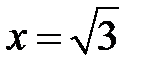 − точка максимума, в точках
− точка максимума, в точках 
 нет экстремума (подразд. 2.10).
нет экстремума (подразд. 2.10).
| Знак производной |
| + |
| + |
| _ |
| x |
| Поведение функции |
| -1 |
| max |
| min |
| -1,7 |
| 1,7 |
| _ |
| + |
| + |

|

|

|

|

|

|

|
| Рис. 6. Интервалы монотонности, точки экстремума |
Значения функции в точках экстремума: 
 Точки
Точки  − точка минимума графика функции,
− точка минимума графика функции,  − точка максимума графика функции.
− точка максимума графика функции.
Интервалы монотонности:  − интервалы убывания функции;
− интервалы убывания функции;  − интервалы возрастания функции.
− интервалы возрастания функции.
На эскиз графика функции нанесем точки минимума  и максимума
и максимума  .
.
III. Исследование функции по второй производной.
Исследуем функцию на выпуклость и точки перегиба.


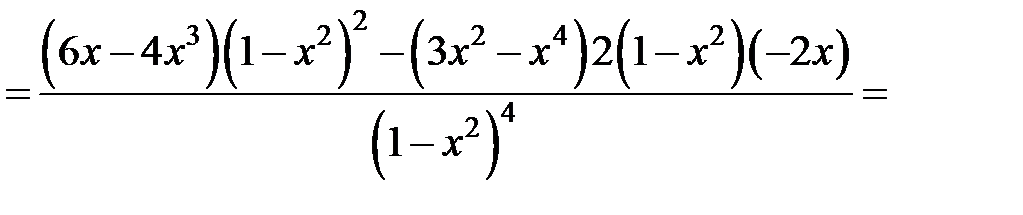

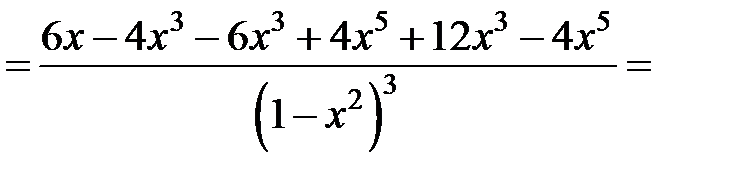

| + |
| Перегиб |
| _ |
| х |
| Поведение функции |
| Знак второй производной |
| _ |
| + |
| -1 |
| Нет перегиба, разрыв |
| Нет перегиба, разрыв |

|

|

|

|

|
| Рис. 7. Интервалы выпуклости, точки перегиба |

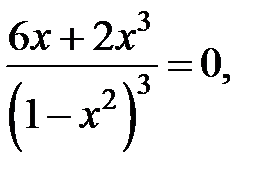

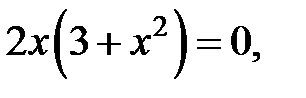
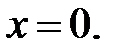 Вторая производная
Вторая производная  не существует в точках
не существует в точках  Следовательно, точка
Следовательно, точка 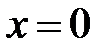
 − критическая точка 2-го рода, точки
− критическая точка 2-го рода, точки 
 и поэтому таковыми не являются.
и поэтому таковыми не являются.| О |
| у |
| х |
| -2,6 |
| -2 |
| -1 |
| пер |
| max |
Рис. 8. График функции 
|
| 1,7 |
| -1,7 |
| min |
| 2,6 |
| у = - х |
| х =1 |
| х = -1 |
 − абсцисса точки перегиба, а в точках
− абсцисса точки перегиба, а в точках 
 точек перегиба график функции не имеет. Значение функции в точке перегиба:
точек перегиба график функции не имеет. Значение функции в точке перегиба:  , следовательно,
, следовательно,  − точка перегиба графика функции. Интервалы вогнутости:
− точка перегиба графика функции. Интервалы вогнутости:  , выпуклости:
, выпуклости: 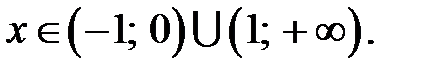
На эскиз графика функции нанесем точку перегиба 
IV. Построение графика функции (рис. 8).
Дополнительные точки:

в) 
Решение.
I. Элементарные исследования.
1. 

2. 



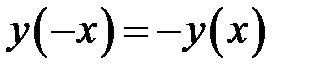
 функция общего положения.
функция общего положения.
3. Функция не является периодической.
4. Точки пересечения с осями координат: при 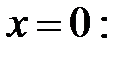

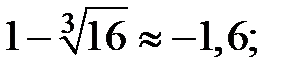
 точка пересечения с осью
точка пересечения с осью  при
при 





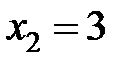 ,
,  и
и  − точки пересечения с осью
− точки пересечения с осью 
| Знак функции |
| _ |
| + |
| _ |
| х |

|

|
| у |
| Рис. 9. Интервалы знакопостоянства |
Значит, на интервалах  график функции ниже оси
график функции ниже оси 
 − выше оси
− выше оси 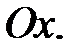
6. Функция является непрерывной на всей числовой оси, так как 

7. Асимптоты графика функции:
а) вертикальных асимптот нет;
б) наклонная асимптота: 

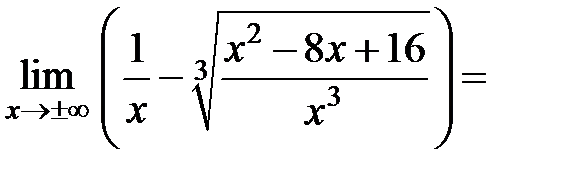
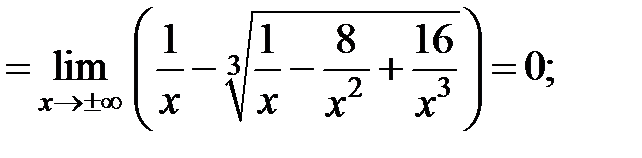

Следовательно, наклонных асимптот нет.
На эскиз графика функции нанесем точки пересечения с осями координат 
 ,
,  , отметим участки, где график лежит выше и ниже оси Ох.
, отметим участки, где график лежит выше и ниже оси Ох.
II. Исследование функции по первой производной.

 .
.
Нет точек, в которых 
 не определена в точке
не определена в точке 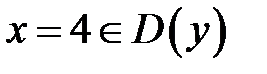 , следовательно,
, следовательно,  − критическая точка 1-го рода.
− критическая точка 1-го рода.
| Знак производной |
| х |
| Поведение функции |
| max |
| _ |
| + |

|
| у |

|
| Рис. 10. Интервалы монотонности,точки экстремума |
 наносим область определения функции и найденные крити-ческие точки. Строим диаграмму исследования функции на экстремум и интервалы монотонности (рис. 10).
наносим область определения функции и найденные крити-ческие точки. Строим диаграмму исследования функции на экстремум и интервалы монотонности (рис. 10).
В точке  − максимум функции;
− максимум функции; 

Интервалы монотонности: при  функция возрастает, при
функция возрастает, при  − убывает.
− убывает.
На эскиз графика функции нанесем точку максимума 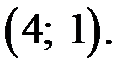
III. Исследование функции по второй производной.

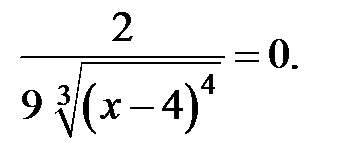 Нет точек, в которых
Нет точек, в которых 
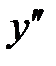 не определена в точке
не определена в точке 

 − критическая точка 2-го рода.
− критическая точка 2-го рода.
На ось 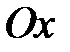 наносим область определения функции и найденные крити-ческие точки. Строим диаграмму исследования функции на точки перегиба и интервалы вогнутости, выпуклости (рис. 11).
наносим область определения функции и найденные крити-ческие точки. Строим диаграмму исследования функции на точки перегиба и интервалы вогнутости, выпуклости (рис. 11).
Точек перегиба нет. На интервалах 
 график функции вогнутый.
график функции вогнутый.
| + |
| + |
| х |
| Поведение функции |
| Знак второй производной |
| Нет перегиба |

|

|

|
| Рис. 11. Интервалы выпуклости, точки перегиба |
Дополнительные точки:
при 
 ; при
; при 
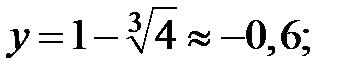
при 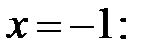
 при
при 

| О |
| у |
| х |
| -1,6 |
| max |
Рис. 12. График функции 
|

г) 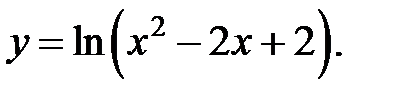
Решение.
I. Элементарные исследования.
1. 
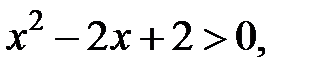
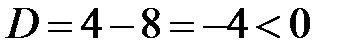
 действительных корней нет.
действительных корней нет.
Следовательно, 
2. Четность, нечетность.





 функция общего положения.
функция общего положения.
3. Функция непериодическая.
4. Точки пересечения с осями координат.
При 

 − точка пересечения с осью
− точка пересечения с осью  (ноль функции).
(ноль функции).
При 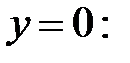


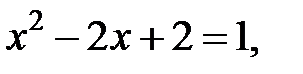
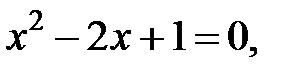



 − точка пересечения с осью
− точка пересечения с осью 
| Знак функции |

|
| + |
| + |
| х |

|
| у |
| Рис. 13. Интервалы знакопостоянства |
Функция принимает положительные значения при любых  Следовательно, график функции выше оси
Следовательно, график функции выше оси 
6. Функция является непрерывной на всей числовой оси.
7. Асимптоты графика функции:
а) вертикальных асимптот нет;
б) наклонная асимптота 



 (воспользовались правилом Лопиталя).
(воспользовались правилом Лопиталя).


 наклонных асимптот нет.
наклонных асимптот нет.
На эскиз графика функции нанесем точки пересечения с осями координат 
 , отметим участки, где график лежит выше и ниже оси Ох.
, отметим участки, где график лежит выше и ниже оси Ох.
II. Исследование функции с помощью первой производной.



 Точек, в которых производная
Точек, в которых производная  не определена, нет, так как
не определена, нет, так как  при
при  . Следовательно,
. Следовательно,  − критическая точка 1-го рода.
− критическая точка 1-го рода.
| Знак производной |
| х |
| Поведение функции |
| min |
| _ |
| + |

|
| у |

|
| Рис. 14. Интервалы монотонности, точки экстремума знакопостоянства |


 − точка минимума.
− точка минимума.
При  − функция убывает, при
− функция убывает, при  − возрастает.
− возрастает.
На эскиз графика функции нанесем точку минимума 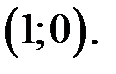
III. Исследование функции с помощью второй производной.







Точек, в которых вторая производная 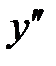 не определена, нет. Следовательно,
не определена, нет. Следовательно, 
 − критические точки 2-го рода.
− критические точки 2-го рода.
| + |
| _ |
| х |
| Поведение функции |
| Знак второй производной |
| Перегиб |

|

|

|
| _ |
| Перегиб |
| Рис. 15. Интервалы выпуклости, точки перегиба |
| у |
| у |
| х |
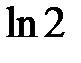
|
| -1 |
| min |
| -2 |
| -3 |
| пер |
| пер |
| О |

|

|
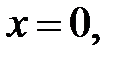
 − абсциссы точек перегиба. Значения функции в точках перегиба
− абсциссы точек перегиба. Значения функции в точках перегиба 
 Следовательно,
Следовательно, 
 − точки перегиба графика функции.
− точки перегиба графика функции.Рис. 16. График функции 
|

 интервал вогнутости:
интервал вогнутости: 
На эскиз графика функции нанесем точки перегиба 

IV. Построение графика функции (рис. 16).
Дополнительные точки: 
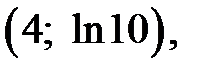

Библиографический список
1. Ф и х т е н г о л ь ц Г. М. Курс дифференциального и интегрального исчисления / Г. М. Ф и х т е н г о л ь ц. М.: Физматлит, 2001. Т. 1. 616 с.
2. П и с ь м е н н ы й Д. Т. Конспект лекций по высшей математике / Д. Т. П и с ь м е н н ы й. М.: Айрис-пресс, 2006. Ч. 1. 288 с.
3. В ы г о д с к и й М. Я. Справочник по высшей математике / М. Я. В ы-
г о д с к и й. М.: Астрель, 2006. 991 с.
4. Б а р а н о в а Е. С. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие / Е. С. Б а р а н о в а, Н. В. В а с и л ь е в а, В. П. Ф е д о т о в. СПб: Питер, 2009. 320 с.
5. К у з н е ц о в а Л. Г. Элементы математического анализа для экономис-тов: Учебное пособие / Л. Г. К у з н е ц о в а / Омский экон. ин-т. Омск, 2005. 184 с.
Учебное издание
АВИЛОВА Лиана Валериевна,
ДОЛГОВА Лариса Вячеславовна
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Часть 2
Учебно-методическое пособие
_______________________________
Редактор Н. А. Майорова
Корректор И. А. Сенеджук



Подписано в печать 29. 10. 2015. Формат 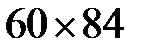 1/16.
1/16.
Офсетная печать. Бумага офсетная. Усл. печ. л.. Уч.-изд. л.
Тираж 1000 экз. Заказ.


Редакционно-издательский отдел ОмГУПСа
Типография ОмГУПСа

644046, г. Омск, пр. Маркса, 35






