Рассмотрим поведение векторов E и D на границе раздела двух однородных изотропных диэлектриков с проницаемостями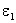 
и 
при отсутствии на границе свободных зарядов.
Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 2.6).
Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность
.
Выделяя потоки через основания и боковую поверхность цилиндра
,
где 
- значение 
касательной составляющей усредненное по боковой поверхности 
. Переходя к пределу при 
(при этом также стремится к нулю), получаем 
, или окончательно для нормальных составляющих вектора электрической индукции 
.
Для нормальных составляющих вектора напряженности поля получим 
.
Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора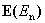 
терпит разрыв, а нормальная составляющая вектора 
непрерывна.
Граничные условия для касательных составляющих векторов D и E следуют из соотношения, описывающего циркуляцию вектора напряженности электрического поля. Построим вблизи границы раздела прямоугольный замкнутый контур длины l и высоты h (рис. 2.7).
Учитывая, что для электростатического поля
,и обходя контур по часовой стрелке, представим циркуляцию вектора E в следующем виде:
,
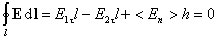где 
- среднее значение En на боковых сторонах прямоугольника. Переходя к пределу при , получим для касательных составляющих E 
Для касательных составляющих вектора электрической индукции граничное условие имеет вид 
Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора 
непрерывна, а касательная составляющая вектора 
терпит разрыв.
Преломление линий электрического поля. Из граничных условий для соответствующих составляющих векторов E и D следует, что при переходе через границу раздела двух диэлектрических сред линии этих векторов преломляются (рис. 2.8). Разложим векторы E1 и E2 у границы раздела на нормальные и тангенциальные составляющие и определим связь между углами 
и 
при условии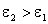 
. Легко видеть, что как для напряженности поля, так и для индукции справедлив один и тот же закон преломления линий напряженности и линий смещения
.
При переходе в среду с меньшим значением 
угол, образуемый линиями напряженности (смещения) с нормалью, уменьшается, следовательно, линии располагаются реже. При переходе в среду с большей линии векторов E и D, напротив, сгущаются и удаляются от нормали.
