Прямая и обратная геодезические задачи
Вычислительная обработка результатов измерений на местности, проводимая при составлении планов, решение ряда землеустроительных задач, подготовка данных для выноса проектов в натуру непосредственно связаны с прямой и обратной геодезическими задачами на координаты.
Прямая геодезическая задача. Сущность данной задачи (рис.2) в следующем: по известным координатам точки 1 (x1, y1), линии 1-2, дирекционному углу этой линии а1-2 и ее горизонтальному проложению d1-2 требуется определить координаты точки 2.

Рис. 2. Прямая и обратная геодезические задачи
Проведя через точки 1 и 2 линии, параллельные координатным осям, получим прямоугольный треугольник 1-2'-2, в котором известны гипотенуза d1-2 и острый угол r = a1-2. Катеты этого треугольника есть приращения координат Δ x и Δ y, которые могут быть получены по формулам:
Δ x = d1-2 cos a1-2 ; Δ y = d1-2 sin a1-2 ; (1)
Контроль: d = 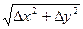 .
.
Следует помнить, что в общем случае знаки приращений координат зависят от четверти, определяемой дирекционным углом заданного направления (см. табл. 1).
Тогда координаты искомой точки 2 определятся по формулам:
x2 = x1 + Δx; y2 = y1 + Δy;
или
x2 = x1 + d1-2 cos a1-2 ; y2 = y1 + d1-2 sin a1-2 .
Приращения координат и координаты искомой точки вычисляются с точностью, соответствующей точности измерения горизонтальной длины линии.
Обратная геодезическая задача. По известным координатам точек 3 (x3, y3) и 4 (x4, y4) требуется определить горизонтальное проложение стороны d3-4 и дирекционный угол направления a3-4.
Согласно рис.2 и формуле (1) можно записать
Δ x = x4 - x3; Δ y = y4 - y3.
По найденным значениям приращений координат Δ x и Δ y, решая прямоугольный треугольник, вычисляют табличный угол:
tg r = 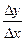 ,
,
отсюда
r = arctg  .
.
По знакам приращений координат Δ x и Δ y определяют, в какой четверти находится данное направление. Затем, руководствуясь соотношением между табличным и дирекционным углами (см. табл. 1), находят дирекционный угол направления. Например, в рассматриваемом случае знаки приращений координат показывают, что направление 3-4 находится в IV четверти, тогда
a3-4. = 360° - r.
Зная дирекционный угол направления и приращения координат, определяют горизонтальное проложение стороны
d3-4 =  =
=  =
= 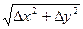 .
.
По этой формуле значение горизонтального проложения стороны определяется трижды; сходимость результатов служит надежным контролем решения задачи. Наибольшее внимание при решении обратной задачи следует уделять вычислению приращений координат Δ x и Δ y
Вычисление длин линий и дирекционных углов по координатам начала и конца линии
| Название отрезков линий | Название концов отрезков | Координаты (м) | Длина линии (м) | Дирекционный угол a° | |||
| Хм | Ум | ОГЗ | Через ГУ | По карте | |||
| 1-2 | |||||||
| 2-3 | |||||||
| 3-4 | |||||||
| 4-1 | |||||||






