Текущие дисконтированные стоимости

РАЗДЕЛ 14. ЭЛЕМЕНТЫ ТЕОРИИ РАЗНОСТНЫХ УРАВНЕНИЙ

· Исследуются разностные уравнения

· Рассматриваются разностные уравнения первого, второго и высших порядков, вопросы устойчивости

РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Для функции , определённой при используем обозначение Пусть функция определена для и всех Будем далее рассматривать разностные уравнения первого порядка, имеющие вид

. (1)

Это уравнение позволяет последовательно находить значения при заданном значении . Однако в ряде случаев удаётся получить формулу, дающую явное значение . Рассмотрим, например, уравнение

(2)

из которого, при заданном значении , находим и далее,

, . (3)

(Проверьте, что равенство (3) справедливо при всех методом математической индукции, используя (2)). В частном случае, когда формула (3) при даёт

, . (4)

Если же 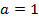, то формула (3) принимает вид

Например, уравнение согласно формуле (4) имеет решение

, а уравнение имеет решение

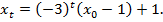
Следующий пример – модель роста экономики. Пусть национальный доход, инвестиции, 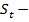сбережения, и пусть , . Тогда

Задачи. Решить следующие разностные уравнения с начальным условием:

ПОЛОЖЕНИЯ РАВНОВЕСИЯ И УСТОЙЧИВОСТЬ

Из формулы (4) следует, что если , то для всех выполняется равенство

. (5)

Более того, из уравнения (2) следует, что если (5) выполняется при некотором значении , то оно выполняется и для остальных значений. Будем говорить, что представляет собой положение равновесия для уравнения .

Пусть в этом уравнении Тогда из (4) следует, что

При этом рассматриваемое уравнение называется глобально асимптотически устойчивым. Отметим, что если , то стремление монотонное, а в случае имеют место затухающие колебания.

Если же в уравнении …, , то

Рассмотрим так называемую паутинообразную модель, в которой и каждому из участников требуется максимизировать .

Для этого должно выполняться условие 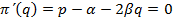, откуда, при . Это даёт величину . Величины изменяются при в соответствии с законом 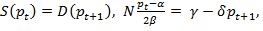откуда

. (6)

Положение равновесия описывается равенством

Решение уравнения (6), по формуле (4), имеет вид

Уравнение (6) устойчиво, если . Если же то в некоторый момент перестанет выполняться неравенство , что будет означать выход участников из процесса. Если же, наконец, , то пара , в зависимости от чётности , принимает два значения ,

ТЕКУЩИЕ ДИСКОНТИРОВАННЫЕ СТОИМОСТИ

Пусть обозначает стоимость активов в конце периода . Если процентная ставка за период времени постоянна и равна , обозначает изъятые средства, а вложенные средства, то

и согласно формуле (32) имеем

, .

или

, .

В нулевой момент времени левая часть этой формулы называется текущей дисконтированной стоимостью.