ОТЧЕТ
По лабораторной работе № 12
Тема: Измерение взаимной индуктивности катушек баллистическим методом
Выполнили студенты группы 33212/3 Бекетаева К. М.
Бокарев И. Д.
Золотухин Е. О.
Руководитель Р.П. Кияткин
«___» _________________ 2016 г.
Санкт-Петербург
Цель и задачи, решаемые в работе:
Целью работы является ознакомление с баллистическим методом измерения взаимной индуктивности, а также с общими принципами расчета взаимной индуктивности катушек.
| 110 B |
| r |
| Вторичная обмотка образцового соленоида |
| Образцовый соленоид |
| Исследуемая катушка |
| Гальванометр |
| Исследуемая катушка |
| mA |
| G |
| К1 |
| К2 |
| К3 |
Рис 1. Схема исследуемой цепи.
Исходные данные: образцовый соленоид
длина l = 1000мм
первична обмотка w1 = 820
вторичная обмотка w2 = 1000
средний диаметр d = 63мм
Постоянная гальванометра: I=200 mA 

 14,586*10-6
14,586*10-6
Снятие баллистическим методом зависимости взаимной индуктивности для двух прямоугольных катушек.
Параметры:
прямоугольные катушки
средняя длина сторон а = 100мм
b = 200мм
ширина катушки с = 22мм
Катушка 1
число витков подвижной катушки w1 = 1000
число витков неподвижной катушки w2 = 475
I=20 mA
Таблица 1. Результаты измерений и расчёта при снятии зависимости взаимной индуктивности для двух прямоугольных катушек от расстояния между ними, в цепи гальванометра неподвижная катушка.
| x, см |  , дел , дел
| Мэксп, Гн | Mтеор, мГн |
| 2,3 | 0,0627 | 65.55 | |
| 2,5 | 0,0620 | 61.6 | |
| 0,0540 | 53.23 | ||
| 3,5 | 0,0467 | 46.48 | |
| 4,5 | 0,0365 | 36.23 | |
| 5,5 | 0,0299 | 28.85 | |
| 7,5 | 0,0219 | 19.14 | |
| 10,5 | 0,0139 | 11.19 | |
| 14,5 | 0,0088 | 6.08 | |
| 19,5 | 0,0066 | 3.2 | |
| 25,5 | 0,0051 | 1.68 | |
| 30,5 | 0,0044 | 1.07 |

Теоретический расчет:
В данной модели каждая из прямоугольных катушек заменяется прямоугольными витками со сторонами a0 и b0, расчет производится методом участков.
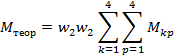


Пример расчета для 1 столбца (расчетный):
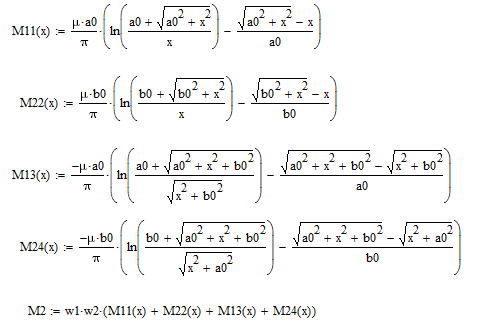
По результатам, представленным в таблице 1, были построены графические зависимости взаимной индуктивности от расстояния между катушками для разных способов расчета:

Катушка 2
число витков подвижной катушки w1 = 1500
число витков неподвижной катушки w2 = 300
I=15 mA
Таблица 2. Результаты измерений и расчёта при снятии зависимости взаимной индуктивности для двух прямоугольных катушек от расстояния между ними, в цепи гальванометра неподвижная катушка.
| x, см |  , дел , дел
| Мэксп, Гн | Mтеор, мГн |
| 2,5 | 0,0652 | 58.36 | |
| 0,0574 | 50.43 | ||
| 3,5 | 0,0486 | 44.03 | |
| 4,5 | 0,0370 | 34.32 | |
| 5,5 | 0,0301 | 27.33 | |
| 7,5 | 0,0194 | 18.13 | |
| 10,5 | 0,0117 | 10.6 | |
| 14,5 | 0,0058 | 5.76 | |
| 19,5 | 3,5 | 0,0034 | 3.03 |
| 25,5 | 0,0019 | 1.59 | |
| 30,5 | 1,5 | 0,0015 | 1.01 |

Теоретический расчет:
В данной модели каждая из прямоугольных катушек заменяется прямоугольными витками со сторонами a0 и b0, расчет производится методом участков.
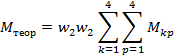


Пример расчета для 1 столбца (расчетный):
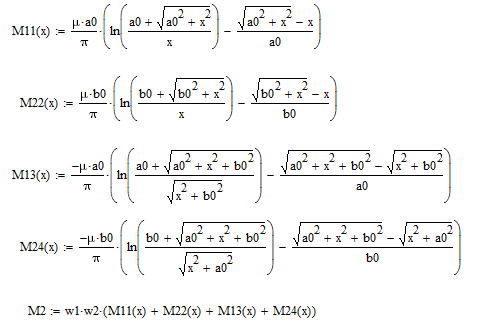
По результатам, представленным в таблице 2, были построены графические зависимости взаимной индуктивности от расстояния между катушками для разных способов расчета:

Снятие баллистическим методом зависимости взаимной индуктивности для двух круглых катушек.
Параметры: круглые катушки
средний диаметр d1 = d2 = 162мм
число витков w1 = w2 = 338
ширина катушки с = 29мм
I=70 mA
Таблица 3. Результаты измерений и расчёта при снятии зависимости взаимной индуктивности для двух круглых катушек.
| Эксперимент | Теоретический расчет | ||||
| x, см | 
| Mэксп,Гн | k^2 | f(k) | Мтеор,Гн |
| 4,3 | 0,0127 | 0,93 | 0.76 | 0,0088 | |
| 4,5 | 0,0117 | 0,93 | 0.76 | 0,0088 | |
| 0,0104 | 0,91 | 0.7 | 0,0081 | ||
| 5,5 | 0,0096 | 0,90 | 0.64 | 0,0074 | |
| 6,5 | 0,0077 | 0,86 | 0.55 | 0,0064 | |
| 8,5 | 0,0054 | 0,78 | 0.35 | 0,0041 | |
| 11,5 | 0,0031 | 0,66 | 0.22 | 0,0026 | |
| 15,5 | 0,0023 | 0,52 | 0.14 | 0,0016 | |
| 21,5 | 0,0015 | 0,36 | 0.06 | 0,0007 | |
| 28,5 | 0,0010 | 0,24 | 0.04 | 0,0005 | |
| 0,0006 | 0,20 | 0.02 | 0,0002 |
Пример расчета для первой строки (экспериментальный):
 =
= 
Теоретический расчет:
Теоретическое значение индуктивности исходной системы было найдено с помощью представления каждой круглой катушки в виде тонкого витка радиуса R0=81 мм
 , где
, где  ,
,  ,
,
По результатам, представленным в таблице 3, были построены графические зависимости взаимной индуктивности от расстояния между катушками для разных способов расчета:

Вывод:
В данной работе были построены экспериментальные и теоретические графики зависимости взаимной индуктивности катушек прямоугольных и круглых сечений от расстояния между ними.
Причиной некоторого расхождения опытных и расчетных кривых, помимо неизбежных погрешностей измерений, может явится сделанная при расчете замена катушек с конечным сечением обмоток эквивалентными весьма тонкими контурами. Очевидно, погрешности, возникающие в результате такого упрощения, будут иметь наибольшее значение при малых расстояниях x между катушками.






