Контрольные работы по РТЦиС
(Баскей В.Я. и др.Радиотехнические цепи и сигналы. Задачи и задания – Новосибирск: Изд-во НГТУ, 2002)
Варианты: Номер варианта контрольного задания определяется по последней цифре номера студента в списке группы. Номер подварианта - по предпоследней цифре номера. Например, студент с №=16 решает вариант 6, подвариант 1; №=6 решает вариант, подвариант 0, студент с №=10 решает вариант 0, подвариант 1, студент с №=20 решает вариант 0, подвариант 2 и т.д.
КОНТРОЛЬНОЕ ЗАДАНИЕ
МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛА
В табл. 1.2 и 1.3 заданы варианты и подварианты импульсного сигнала.
Требуется:
Записать математическую модель сигнала S(t)через временные интервалы и на непрерывной оси времени с помощью комбинаций (суммы и произведений) функций Хевисайда.
Таблица 1.2
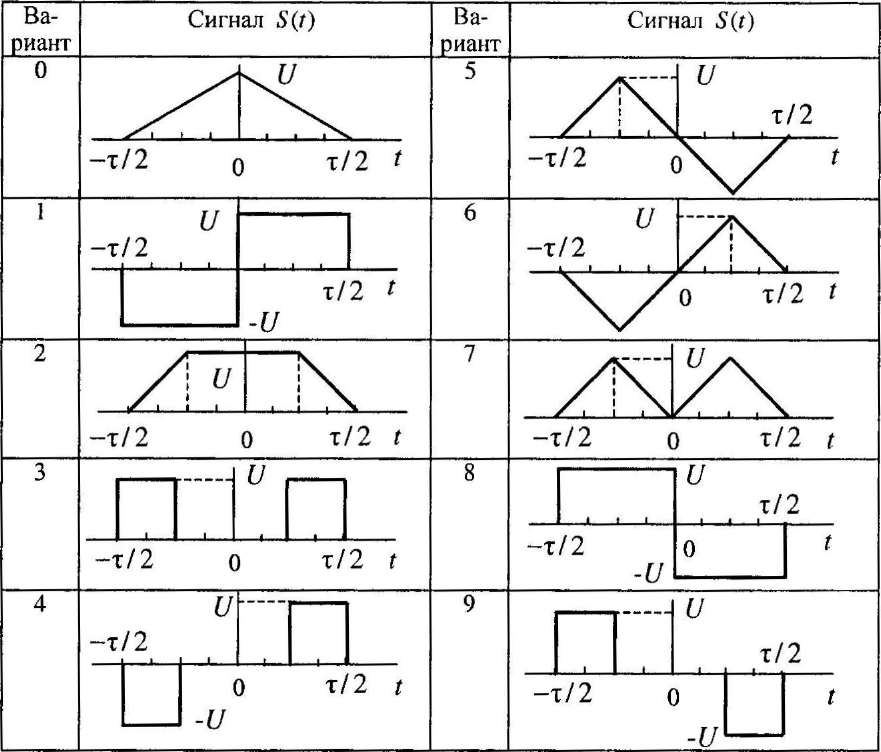
Таблица 1.3
| Подвариант | ||||||||||
| U, В | ||||||||||
| τ, мс | ||||||||||
| T, мс |
ПРЕДСТАВЛЕНИЕ СИГНАЛА В БАЗИСЕ ФУНКЦИЙ УОЛША
Аппроксимируйте сигнал 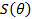 в базисе 8 ФУ wal(n,
в базисе 8 ФУ wal(n, 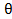 ), п = О,...,7. Форма сигнала задана в табл. 1.4, а параметры приведены в табл. 1.5.
), п = О,...,7. Форма сигнала задана в табл. 1.4, а параметры приведены в табл. 1.5.
Требуется:
а) определить спектр и построить спектральную диаграмму для заданного 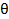 0 и
0 и 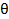 0 = 0;
0 = 0;
б) синтезировать сигнал на интервале [0, 1] и построить на одном графике заданную и аппроксимированную функцию для  0 = 0;
0 = 0;
в) рассчитать норму и энергию (на сопротивлении 1 Ом) исходного и аппроксимированного сигнала;
г) определить относительную среднеквадратическую ошибку аппроксимации.
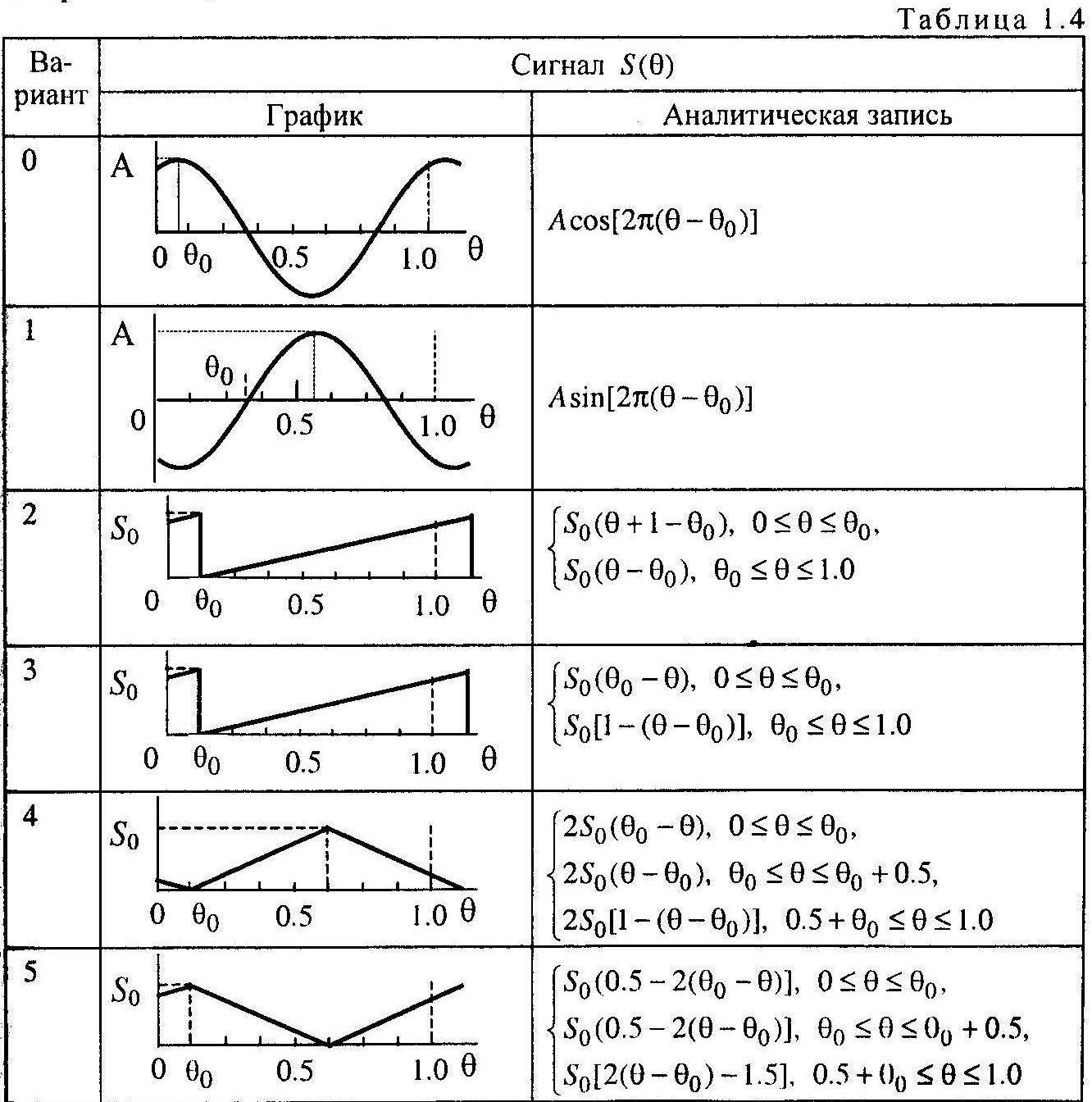

Таблица 1.5
| Вариант | ||||||||||

| 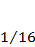
| 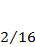
| 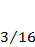
| 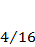
| 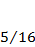
| 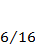
| 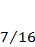
| 
| 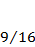
| 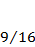
|
 или или 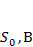
|
КОНТРОЛЬНОЕ ЗАДАНИЕ
Спектральный анализ сигналов
В табл. 1.2 заданы варианты импульсных сигналовS(t), а в табл.1.3 - их параметры.
Требуется:
а) определить спектральную плотность 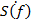 сигналаS(t). Построить спектральные диаграммы модуля|S(f)|и фазы φ(f), диаграмму энергетического спектра |S(f)|2;
сигналаS(t). Построить спектральные диаграммы модуля|S(f)|и фазы φ(f), диаграмму энергетического спектра |S(f)|2;
б) найти ширину "лепестка" спектра сигнала; для вариантов 1, 3...9 также ширину "лепестка" спектра одиночного импульса, входящего в состав сигнала;
в) вычислить энергию сигнала;
г) рассчитать коэффициенты 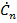 и
и 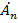 комплексного и тригонометрического ряда Фурье для периодического сигналаST(t), полученного путем повторения заданного сигнала S(t)с периодом Тп. Построить соответствующие спектральные диаграммы |
комплексного и тригонометрического ряда Фурье для периодического сигналаST(t), полученного путем повторения заданного сигнала S(t)с периодом Тп. Построить соответствующие спектральные диаграммы |  |,
|, 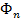 и |
и | 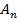 |,
|, 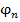 .
.
МЕТОДИЧЕСКАЕ УКАЗАНИЯ
При выполнении первого пункта задания следует иметь в виду, что непосредственное применение прямого преобразования Фурье для некоторых вариантов приводит к сложному и громоздкому интегрированию. Поэтому для получения результата наиболее простым путем целесообразно использовать теоремы о спектрах (см. прил. П.4), например теоремы о спектре суммы и производной сигналов. После n-кратного дифференцирования сигнала, описываемого кусочно-линейными функциями времени, результат выражается с помощью различных комбинаций функций Хевисайдаσ(t) и Диракаδ(t), спектральные плотности которых хорошо известны [1]. Кратность дифференцирования n следует выбирать такой, чтобы не потребовалось дифференцировать функцию δ(t).
При выполнении четвертого пункта следует учесть известную связь между спектральной плотностью одиночного импульса и спектром периодического сигнала (см. формулы (2.10) и (2.5)).
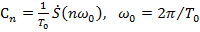 (2.10)
(2.10)
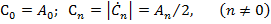 ; (2.5)
; (2.5)
ЭЛЕМЕНТЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
В табл. 1.2 и 1.3 заданы варианты и подварианты импульсных сигналов S(t).
Требуется:
а) вычислить автокорреляционную функцию (АКФ) и построить графикК(τ);
б) рассчитать энергетический спектр импульса |S(f)|2с помощью АКФ.






