Для построения термодинамической теории процесса ректификации требуется определенная его идеализация, различная для тарельчатой и насадочной колонны. Для тарельчатой колонны используется концепция теоретической тарелки; для насадочной эта концепция заменяется концепцией единицы переноса, потому что в насадочной колонне, в отличие от тарельчатой, происходит непрерывный контакт фаз.
Число единиц переноса (ЧЕП) по i-тому компоненту N pi определяется, как известно, следующим образом:
 (1)
(1)
где y* - равновесная концентрация;
y – рабочая концентрация;
yн yк – начальная и конечная концентрации.
В дифференциальной форме:
 (2)
(2)
Вывод расчетного уравнения для режима полного орошения сложной насадочной колонны предложен Андервудом. На любом уровне насадочной колонны в режиме полного орошения встречные фазы должны максимально отступать от состояния равновесия, поэтому составы газовой и жидкой фазы одинаковы. Для произвольного компонента это запишется в виде:
 (3)
(3)
Из уравнения фазового равновесия:
 (4)
(4)
Заменяя константу равновесия относительной летучестью, получим
 (5)
(5)
где kэ – константа равновесия эталонного компонента. С учетом уравнений (3-5) можем преобразовать уравнение (2) к виду:
 (6)
(6)
Если написать n уравнений (6) по числу компонентов системы, то правые части всех этих уравнений будут одинаковы. Поэтому можно попарно приравнять их левые части и для двух любых произвольных компонентов записать:
 (7)
(7)
Интегрируя уравнение (7) и решая его относительно ЧЕП, получаем:
 (8)
(8)
Если допустить, что по какому-либо компоненту i продуктовые концентрации известны, то можно определить продуктовые концентрации неизвестного компонента k. Рассчитывая из уравнения:
 (9)
(9)
отношение концентраций xWk и xDk, можно итерационным методом определить состав дистиллята и кубового остатка:
 (10)
(10)
Итерации заканчиваются, если для значений продуктовых концентраций выполняются равенства:
 (11)
(11)
Это означает, что предварительно принятые величины xDi и xWi были выбраны правильно.
Расчет диаметра 1
Диаметр насадочной колонны можно определять по скорости паров в свободном сечении колонны в точке захлебывания по эмпирической корреляции Шервуда:
 (12)
(12)
где:


a – удельная поверхность насадки, м2/м3;
Vc –свободный объем насадки.
Значение коэффициента А, соответствующее точке захлебывания определяется типом насадки, так для керамических колец Рашига А =1,2.
Рабочая скорость пара в свободном сечении колонны должна составлять 65-85% от скорости захлебывания, то есть:
 (13)
(13)
Диаметр любой из частей колонны:
 или
или  (14)
(14)
где V – объемный расход пара.
Режимы работы колонн
В насадочной колонне потоки жидкости и пара взаимодействуют в противотоке. При малых нагрузках взаимодействие между фазами незначительно и сопротивление насадки пропорционально сопротивлению сухой насадки. Такой режим называют пленочным. При дальнейшем увеличении скоростей потоков возрастает трение между фазами, происходит торможение жидкости и увеличение времени ее пребывания в насадке. Этот режим характеризует начало подвисания жидкости, он принимается в качестве нижнего предела устойчивой работы колонны. При больших нагрузках по жидкости его не всегда легко выявить. Сопротивление насадки в этом режиме пропорционально скорости пара в 3-4 степени. Интенсивность массопередачи в этом режиме значительно возрастает. Дальнейшее увеличение скоростей фаз приводит к захлебыванию колонны. Эта нагрузка считается верхним пределом устойчивой работы колонны. Вблизи точки захлебывания происходит инверсия фаз, которая сопровождается резким ростом интенсивности массопередачи. Такой режим работы называют режимом эмульгирования. Работа насадочной колонны в этом режиме требует качественной автоматизации процесса и применения тонкостенных насадок. Аналогичные режимы работы характерны и для тарельчатой колонны.
Расчет диаметра 2
Кроме метода, описанного выше, диаметр насадочной колонны можно рассчитать с использованием эмпирических корреляций для гидравлических сопротивлений слоя насадки http://www.cisp.spb.ru/solutions-chemical-engineering/

Для этого рассчитывается значение:
 (15)
(15)
где:
ρV, ρL – плотности жидкого и парового потоков при средних температуре и давлении в колонне, кг/м3;
LW, VW – массовые расходы жидкого и парового потоков в соответствующей части колонны, кг/с.
На рисунке под кривыми приведены значения потерь напора в мм Н2О на 1м высоты слоя насадки. Для предварительных расчетов рекомендуется принять это значение в интервале (20-40). По номограмме определяют коэффициент К4 для заданного значения сопротивления и К4f в режиме захлебывания (верхняя кривая). Далее вычисляется значение, %:
 (16)
(16)
рассчитывается массовый расход паровой фазы на единицу площади поверхности насадки:
 (17)
(17)
где а – удельная поверхность насадки, м-1; μL – вязкость жидкости при средних температуре и давлении в колонне, Н*с/м2.
Рассчитываем необходимую площадь поперечного сечения насадочной колонны, м2:
 (18),
(18),
после чего определяется диаметр колонны:
 (19)
(19)
Диаметр колонны округляют до ближайшего стандартного, как правило, меньшего, для которого проверяется выполнение условия:
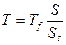 (20),
(20),
где Ss – площадь поперечного сечения колонны ближайшего стандартного диаметра. Параметр Т должен лежать в пределах 50-85% поперечного сечения колонны, работающей в режиме захлебывания. Если условие (20) не выполняется, выбирается насадка большего размера (с меньшей удельной поверхностью) и/или больший стандартный диаметр колонны и расчет повторяется.






