Пример
Для заданного стержня построить эпюры поперечных сил и изгибающих моментов.
Решение.
1. Рассмотрим стержень, нагруженный силами, лежащими в одной плоскости (рис. 3а). Эту плоскость называют силовой. Предположим, что силовая плоскость совпадает с плоскостью, проходящей через ось стержня и одну из главных центральных осей сечения, т.е. является главной плоскостью. Понятие о главных центральных осях вводится при рассмотрении геометрических характеристик сечения. Данное предположение необходимо, чтобы правильно определить вид нагружения, и в дальнейшем специально оговариваться не будет.
Выберем расчетную схему в виде оси стержня, на которую перенесем все действующие внешние силовые факторы (рис. 3б).
Найдем равнодействующую нагрузки, распределенной на участке СВ (на рис. 3б изображена пунктиром):
Р1 = 40 · 2 = 80 кН.
Напомним, что равнодействующую параллельных сил прикладывают в центре тяжести участка, на котором действует распределенная нагрузка. В нашем примере – по середине участка СВ.
| z |
| y |
| x |
| z |
| 2 м |
| 2 м |
| q=40 кН/м |
| М1=20 кН·м |
| а) |
| 15 |
| M1=20кН·м |
| Pq |
|
| 3 м |
| z |
| у |
| q=40 кН/м |
| z |
| А |
| B |
| С |
| P1 |
| RB |
| z |
| 2 м |
| 2 м |
| 2,375 м |
| Q ,кН |
| 65 |
| 20 |
| 50 |
| 52,8 |
| б) |
|
| М, кН·м |
Рис. 3
В соответствии с видом связей изображаем реакции, выбираем систему координат и составляем уравнения статики, из которых определяем величину и направление реакций связей:
ΣМА = - М1 - Р1 · 3 + RВ · 4 = – 20 – 80 · 3 + RВ · 4 = 0; RВ =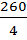 
= 65 кН.
ΣМВ = - М1 - 
· 4 + Р1 · 1 = – 20 – · 4 + 80 · 1 = 0; = 
= 15 кН.
ΣFZ = 
= 0; = 0.
Для проверки правильности полученных значений реакций можно использовать условие равенства нулю суммы проекций всех сил на вертикальную ось и условие равенства нулю суммы моментов всех силовых факторов относительно любой точки, отличной от точек А и В, например, относительно точки С.
Получаем: ΣFY = - Р1 + RВ = 15 – 80 + 65 = 0;
ΣМC = - М1 - · 2 + Р1 · 1 + RВ · 2 = - 20 – 15 · 2 - 80 · 1 + 65 · 2 = 0.
2. Разбиваем стержень на участки. В рассматриваемом примере два участка АС и СВ.
3. На каждом участке методом сечений определяем внутренние силовые факторы.
Рассмотрим участок АС. Рассечем стержень на две части сечением на расстоянии z от начала координат (от т. А) и правую часть мысленно отбросим. Вся нагрузка расположена в плоскости yz (рис. 3), причем силы параллельны оси у (учтено, что = 0), поэтому при составлении условий равновесия отсеченной части внешние силовые факторы не дают проекции на оси z и х (на рисунке не показана) и не создают моменты относительно осей у и z (рис. 3а). Следовательно, в любом сечении стержня равны нулю четыре внутренних силовых фактора:
N = QX = MY = MZ = 0.
Отличными от нуля остаются только поперечная сила QY и изгибающий момент MХ. Эти внутренние силовые факторы лежат в силовой плоскости (в плоскости yz). Их часто обозначают без индекса осей.
Таким образом, в рассматриваемом примере в любом поперечном сечении стержня могут возникать только два внутренних силовых фактора – поперечная сила QY и изгибающий момент MХ, т.е. имеет место поперечный изгиб.
Из метода сечений следуют следующие правила определения внутренних силовых факторов при поперечном изгибе:
Поперечная сила Q в рассматриваемом сечении равна алгебраической сумме проекций на поперечную ось (ось y ) всех сил, действующих на рассматриваемую часть стержня.
Изгибающий момент в рассматриваемом сечении равен алгебраической сумме моментов относительно рассматриваемого сечения (относительно оси х, перпендикулярной плоскости чертежа на рис. 3б) от всех силовых факторов, действующих на рассматриваемую часть стержня.
Правила знаков для поперечной силы Q и изгибающего момента М удобно пояснить графически (рис. 4).
Q  0
|
Q  0
|
| M 0
|
| M 0
|
| Mвнешн. |
| Mвнешн. |
| Mвнешн. |
| Mвнешн. |
Рис. 4
Если внешняя сила расположена слева от сечения и направлена вверх (отбрасывают правую часть стержня), то поперечную силу в сечении считают положительной, если сила направлена вниз – отрицательной (рис. 4а). Для сил, расположенных справа от сечения, правило знаков обратное.
Для изгибающих моментов правило знаков следующее:
Если момент от внешнего силового фактора (от сосредоточенной силы, от распределенной нагрузки, от сосредоточенного момента), действующего на левую часть стержня, направлен по ходу часовой стрелки, то внутренний изгибающий момент в сечении считают положительным, если против хода часовой стрелки – отрицательным (рис. 4б). Для моментов, расположенных справа от сечения, правило знаков обратное.
При использовании приведенных правил знаки поперечных сил и изгибающих моментов не зависят от того, какую часть стержня отбрасывают.
Запишем аналитические выражения для поперечной силы и изгибающего момента на участке АС, пользуясь сформулированными выше правилами. Рассмотрим сечение в пределах участка АС на расстоянии z от начала координат (от т. А). Правую часть отбрасываем. Абсцисса сечения z изменяется в пределах 0 ≤ z ≤ 2 м. Для поперечной силы получаем:
Q = = 15 кН.
Знак «плюс», т.к. была отброшена правая часть стержня и реакция направлена вверх (рис. 4).
Изгибающий момент будет равен:
М = М1 + · z = 20 + 15 · z (кН·м).
Знаки выбраны в соответствии с рис. 4.
Изгибающий момент на участке АС изменяется по линейному закону. График – прямая линия. Для ее построения достаточно найти две точки. Получаем:
МZ=0 = 20 кН·м; МZ=2 = 20 + 15 · 2 = 50 кН·м.
Выбираем ось отсчета и строим эпюры. Положительные значения внутренних силовых факторов откладываем от оси сечения вверх. Отрицательные – вниз (рис. 3б).
Рассмотрим участок СВ. Проведем сечение в пределах этого участка (рис. 3б). Абсцисса z на этом участке изменяется в пределах 2 ≤ z ≤ 4 м. Так как участок стержня длиной z включает часть распределенной нагрузки, то заменяем эту нагрузку ее равнодействующей Рq = q (z – 2). Равнодействующую Рq помещаем в центр тяжести учитываемой распределенной нагрузки, т.е. по середине отрезка (z - 2).
Для поперечной силы получаем:
Q = - Рq = 
q (z – 2) = 15 - 40· (z – 2).
Изгибающий момент равен:
М = М1 + · z - Рq · 
= 20 + 15z – 40 · (z – 2) · = 20 + 15z – 20(z – 2)2.
Поперечная сила изменяется по линейному закону. Вычисляем ее значения в начале и в конце участка:
QZ=2 = 15 кН; QZ=4 = 15 – 40 · (z - 2) = 15 – 40 · (4 - 2) = - 65 кН.
По полученным значениям строим эпюру поперечных сил.
Изгибающий момент изменяется по закону квадратной параболы. Определяем значения изгибающего момента в начале и в конце участка:
МZ=2 = 20 + 15 · 2 = 50 кН·м; МZ=4 = 20 + 15 · 4 – 20 · (4 – 2)2 = 0.
Для определения абсциссы точки экстремума вычисляем первую производную от функции, характеризующей закон изменения изгибающего момента на участке СВ, и приравниваем ее к нулю:
= 15 – 40 · (z – 2) = 0; z = 2,375 м.
Вычисляем изгибающий момент в точке экстремума и строим эпюру изгибающих моментов:
МZ=2,375 = 20 + 15 · 2,375 – 20 · (2,375 – 2)2 = 52,8 кН·м.
Для контроля правильности построения эпюр поперечных сил и изгибающих моментов используем дифференциальные зависимости:
= q (1), = Q (2).
Рассмотрим эпюру поперечных сил. На участке АС распределенная нагрузка отсутствует, т.е. q = 0, поэтому тангенс угла наклона касательной к графику поперечной силы, равный первой производной от поперечной силы, согласно формуле (1) должен быть равен нулю. Следовательно, касательная и весь график должны быть параллельны оси отсчета, что и имеет место. На участке СВ
тангенс угла наклона касательной к графику поперечной силы отрицателен и постоянен в пределах этого участка. Согласно формуле (1) и интенсивность распределенной нагрузки q должна быть отрицательной (направленной вниз) и по длине участка не изменяться, что и соответствует расчетной схеме.
Рассмотрим эпюру изгибающих моментов. На участке АС тангенс угла наклона касательной к графику изгибающего момента положителен и постоянен в пределах участка. Следовательно, согласно зависимости (2) должна быть положительна и постоянна поперечная сила на этом участке, что соответствует эпюре поперечных сил. На участке СВ тангенс угла наклона касательной к графику изгибающего момента уменьшает свое положительное значение до нуля (в точке максимума), а затем становится отрицательным, изменяясь в пределах участка. Следовательно, и поперечная сила должна изменять свое положительное значение до нуля, а затем становиться отрицательной, изменяясь в пределах участка. Именно такой характер изменения поперечной силы и имеет место.
Обратим внимание, что в соответствии с формулой (2) первая производная от изгибающего момента равна поперечной силе и, следовательно, в сечениях, где поперечная сила равна нулю, на эпюре изгибающих моментов имеет место экстремум. Поэтому при построении эпюры изгибающих моментов исследование на экстремум можно не проводить (не вычислять первую производную, приравнивать ее нулю и т.д.), а определять абсциссы сечений, где имеет место экстремум, приравнивая поперечную силу нулю.
В заключении отметим общие закономерности при построении эпюр поперечных сил и изгибающих моментов:
1. Если прямой стержень нагружен силами и парами сил, лежащими в главной плоскости, причем сосредоточенные и распределенные силы перпендикулярны к оси стержня, то имеет место поперечный изгиб, т.е. в поперечных сечениях возникают только два внутренних силовых фактора – поперечная сила Q и изгибающий момент М;
2. В сечениях, где приложены сосредоточенные силы, перпендикулярные к оси стержня, на эпюре поперечных сил имеет место скачок на величину этих сил.
3. В сечениях, где приложены сосредоточенные моменты, на эпюре изгибающих моментов имеет место скачок на величину этих моментов.
4. В сечениях, где поперечная сила равна нулю, на эпюре изгибающих моментов имеет место экстремум, т.е. изгибающий момент достигает максимума или минимума.
Содержание
1 Введение ………………………………………………………………………3
2 Алгоритм определения внутренних силовых факторов…………………….4
3 Построение эпюр внутренних силовых факторов
3.1 Построение эпюр продольных сил……………………………………….4
3.2 Построение эпюр крутящих моментов………………………..………...7
3.3 Построение эпюр продольной силы и изгибающих моментов………..10
