МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ
С.П. Борисов, Т.Н. Хромых
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ПОСОБИЕ
по проведению практических занятий
для студентов II курса
направления 25.03.01
всех форм обучения
Москва - 2015
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА)
Кафедра технической механики и инженерной графики
С.П. Борисов, Т.Н. Хромых
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ПОСОБИЕ
по проведению практических занятий
для студентов II курса
направления 25.03.01
всех форм обучения
Москва - 2015
Рецензент д-р техн. наук, профессор Ю.В. Петров
Борисов С.П., Хромых Т.Н.
Сопротивление материалов: пособие по проведению практических занятий «Построение эпюр внутренних силовых факторов при растяжении-сжатии, кручении и поперечном изгибе». – М.: МГТУ ГА, 2015. – 15 стр.
Данное пособие издается в соответствии с рабочей программой учебной дисциплины «Сопротивление материалов» по учебному плану для студентов II курса направления 25.03.01 всех форм обучения.
Рассмотрено и одобрено на заседаниях кафедры 28.04.15 г. и методического совета по направлению 12.05.2015 г.
Введение
Пособие предназначено для студентов при их самостоятельной подготовке к практическим занятиям и при выполнении контрольных домашних заданий по курсу «Сопротивление материалов» в соответствии с учебной программой курса. В пособии рассмотрены методики построения эпюр внутренних силовых факторов при растяжении-сжатии, кручении и поперечном изгибе. Определение внутренних силовых факторов является необходимым элементом расчетов на прочность и жесткость. В зависимости от того, сколько и какие внутренние силовые факторы возникают в поперечном сечении, квалифицируют и виды нагружения.
Алгоритм определения внутренних силовых факторов
Эпюрой внутреннего силового фактора называют график, изображающий закон изменения рассматриваемого силового фактора по длине стержня. Для построения эпюр внутренних силовых факторов необходимо:
1. Определить все внешние силовые факторы, действующие на рассматриваемый стержень, включая реакции связей.
2. Выбрать расчетную схему обычно в виде осевой линии стержня, на которую перенести все силы.
3. Разбить расчетную схему на участки. Границами участков являются места приложения сосредоточенных сил и моментов или изменения закона распределения нагрузок, заданных интенсивностью q.
4. Для каждого участка методом сечений определить внутренние силовые факторы, записав математически законы изменения силовых факторов по длине участка.
5. Выбрать оси отсчета в виде линий, параллельных оси стержня. По математическим выражениям для законов изменения внутренних силовых факторов с учетом специально вводимых правил знаков построить графики, изображающие изменение внутренних силовых факторов по длине стержня, т.е. эпюры.
Напомним метод сечения. Для определения внутренних силовых факторов этим методом необходимо:
1. Рассечь стержень в рассматриваемом сечении на две части…….(Р).
2. Одну из частей (любую) отбросить ……..………………...............(О).
3. Заменить действие отброшенной части на оставшуюся внутренними силовыми факторами…………….…….………..………………………..………(З).
4. Составить условия равновесия рассматриваемой части стержня (уравновесить)………...……….………………………………………………...(У).
Записанный алгоритм для запоминания можно сформулировать как правило РОЗУ по первым буквам слов, обозначающих необходимые действия.
Рассмотрим примеры построения эпюр внутренних силовых факторов при растяжении-сжатии, кручении и изгибе.
Построение эпюр внутренних силовых факторов
Построение эпюр продольных сил
Пример
Для заданного стержня построить эпюру продольных сил (рис. 1а).
Решение.
1. В соответствии с общим алгоритмом прежде всего определяем все внешние силовые факторы, действующие на рассматриваемый стержень (рис. 1а).
Активные силы заданы. Определим реакции связей. В рассматриваемом примере связью является заделка. В заделке при плоской системе сил в общем случае возникают три реакции – две силы и момент. Однако, в данном примере активные силы приложены на оси стержня и действуют вдоль оси, представляющей прямую линию. Равнодействующая активных сил направлена вдоль этой прямой и может быть уравновешена силой, действующей также вдоль этой прямой. Таким образом, возникает только одна реакция, направленная вдоль оси стержня. Выбираем систему координат YOZ, изображаем реакцию связи  , и так как направление ее неизвестно, предварительно направляем ее слева направо. Величину и истинное направление реакции
, и так как направление ее неизвестно, предварительно направляем ее слева направо. Величину и истинное направление реакции  определяем из уравнения статики (рис. 1а):
определяем из уравнения статики (рис. 1а):
ΣFZ = 0;  – P3 – P2 + P1 =
– P3 – P2 + P1 =  – 7 – 3 + 5 = 0;
– 7 – 3 + 5 = 0;  = 5 кН.
= 5 кН.
Если при решении уравнения результат получают со знаком «минус», то направление реакции  изменяют на обратное (влево от т. А).
изменяют на обратное (влево от т. А).
2. Так как в рассматриваемом примере все силы приложены на оси и действуют вдоль нее, то уточнять расчетную схему не следует.
3. Разбиваем стержни на участки, проводя вертикальные линии через точки приложения сосредоточенных сил. Получаем три участка АВ, ВС и СD.
4. На каждом участке методом сечений определяем внутренние силовые факторы.
Рассмотрим участок АВ. Рассечем стержень на две части поперечным сечением на расстоянии z от начала координат (от т. А) и правую часть отбросим (рис. 1б). Абсцисса z в пределах участка АВ изменяется от 0 до 1 м, т.е. 0 ≤ z ≤ 1. На рассматриваемую часть стержня действует только внешняя сила  , направленная вдоль оси стержня. Эта сила может быть уравновешена силой, также действующей вдоль оси стержня, т.е. продольной силой N. Прикладываем в рассматриваемом сечении продольную силу N. Так как направление силы N неизвестно (от сечения или на сечение), то направляем ее вдоль оси произвольно, например, от сечения. Записываем уравнение статики (составляем условие равновесия) для
, направленная вдоль оси стержня. Эта сила может быть уравновешена силой, также действующей вдоль оси стержня, т.е. продольной силой N. Прикладываем в рассматриваемом сечении продольную силу N. Так как направление силы N неизвестно (от сечения или на сечение), то направляем ее вдоль оси произвольно, например, от сечения. Записываем уравнение статики (составляем условие равновесия) для
рассматриваемой части стержня:
ΣFZ = 0;  + N = 5 + N = 0; N = - 5 кН.
+ N = 5 + N = 0; N = - 5 кН.
| y |
| A |
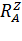
|
| P3=7 кН |
| P2=3 кН |
| P1=5 кН |
| z |
| B |
| C |
| D |
| I |
| I |
| II |
| II |
| III |
| III |
| 1 м |
| 0,5 м |
| 0,5 м |
| z |
| а) |
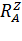 =5 кН =5 кН
|
| N |
| б) |
| z |
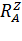 =5 кН =5 кН
|
| P3=7 кН |
| N |
| в) |
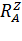 =5 кН =5 кН
|
| P3=7 кН |
| P2=3 кН |
| N |
| г) |
| z |
| N, кН |
| д) |
Рис. 1
Знак «минус» означает, что сила N должна действовать на сечение. Так как сила N не зависит от абсциссы z, то продольная сила по длине участка АВ не изменяется.
5. Выбираем ось отсчета в виде линии, параллельной оси стержня. При построении эпюры продольных сил принимают следующее правило знаков:
Продольную силу N считают положительной, если имеет место растяжение ( N направлена от сечения) и отрицательной, если сжатие ( N направлена на сечение).
При горизонтальном расположении оси отсчета положительные значения продольной силы откладывают вверх, отрицательные – вниз. Так как на участке АВ сила N действует на сечение, т.е. имеет место сжатие, то график изменения N на участке АВ представляет собой прямую, параллельную оси отсчета в отрицательной области значений (рис. 1д).
Рассмотрим участок ВС (рис. 1в, сеч. II-II). Абсцисса z при начале координат в т. А будет изменяться от 1 м до 1,5 м. Рассуждая так же, как и в предыдущем случае, убеждаемся, что в сечении II-II действует только продольная сила N. Записываем уравнение статики для рассматриваемой части стержня:
ΣFZ = 0;  – P3 + N = 5 – 7 + N = 0; N = 7 – 5 = 2 кН.
– P3 + N = 5 – 7 + N = 0; N = 7 – 5 = 2 кН.
Эпюра продольной силы на участке ВС представляет собой прямую, параллельную оси отсчета в положительной области значений (рис. 1д).
Аналогично можно найти продольную силу и на участке СD.
Из эпюры продольных сил следует (рис. 1д), что в точках А, В, С и D значения продольной силы изменились скачком на величину сосредоточенных сил в этих точках. Эта закономерность справедлива при действии любой сосредоточенной силы и значительно облегчает построение эпюр продольных сил для стержней, нагруженных сосредоточенными силами.
Так, для рассмотренного примера можно было бы поступить следующим образом.
Рассмотрим стержень, начиная с т. А (слева направо). В т. А в соответствии с отмеченной закономерностью должен быть скачок на величину  . Сила
. Сила  в сечении I-I (рис. 1а) может быть уравновешена внутренней силой N, равной по модулю
в сечении I-I (рис. 1а) может быть уравновешена внутренней силой N, равной по модулю  и направленной на сечение, т.е. имеет место сжатие и ординату откладываем вниз от оси отсчета (скачок направлен вниз). Если выбрать другое сечение в пределах участка АВ, то результат не изменится. Таким образом, на участке АВ имеем:
и направленной на сечение, т.е. имеет место сжатие и ординату откладываем вниз от оси отсчета (скачок направлен вниз). Если выбрать другое сечение в пределах участка АВ, то результат не изменится. Таким образом, на участке АВ имеем:
NАВ = -  = - 5 кН.
= - 5 кН.
График представляет собой прямую, параллельную оси отсчета.
В т. В должен быть скачок на величину силы P3. Так как сила P3 направлена в сторону, противоположную силе  , то скачок направлен вверх и продольная сила на участке ВС равна:
, то скачок направлен вверх и продольная сила на участке ВС равна:
NВС = NАВ + 7 = -5 + 7 = 2 кН.
Учитывая скачок в т. С, для участка CD получаем:
NCD = NВС + 3 = 2 + 3 = 5 кН.
Если учесть скачок в точке D от силы P1, то находим:
NCD - P1 = 5 – 5 = 0,
что и должно быть, т.к. Σ FZ = 0.
В заключении отметим основные закономерности:
1. В поперечных сечениях прямого стержня, нагруженного силами, приложенными на оси стержня и направленными вдоль оси, возникает только один внутренний силовой фактор – продольная сила N, т.е. имеет место растяжение или сжатие.
2. В сечениях, где приложены сосредоточенные силы, действующие вдоль оси стержня, на эпюре продольных сил имеет место скачок на величину этих сил.
3. Форма и размеры поперечных сечений не влияют на величину продольных сил.
4. Правило нахождения продольной силы для прямых стержней:
Продольная сила в рассматриваемом сечении равна алгебраической сумме проекций на продольную ось всех сил, действующих на рассматриваемую часть стержня. Проекцию любой силы берут со знаком «плюс», если соответствующая ей внутренняя продольная сила направлена от сечения, и «минус» - если на сечение.
Замечание: Это правило справедливо для любой системы внешних сил. В случае криволинейных стержней силы проектируют на ось, перпендикулярную рассматриваемому сечению.






