1. Локализуем, построив в заданном интервале переменной x, график функции F(x), и определим грубую оценку значений корней уравнения F(x)=0.
Отметим, что у полинома третьего порядка имеется не более трёх, вещественных корней.
 |
Построим таблицу (табл. 1, рис. 4.), протабулировав функцию (2) в заданном интервале [-1;1], с шагом табуляции равным +0,2 (рис. 4) и построим график этой функции (рис. 1).
Напоминаем, что в терминах MS Excel в клетке c7, эта формула запишется как формула (3) и ею, используя команду Главная, Заполнить, … нужно будет разместить в остальные клетки интервала c7:c17.
=B7^3-0,01*B7^2-0,7044*B7+0,139104 (3)
Из таблицы 1 и графика (рис. 4) видно, что полином меняет знак в интервалах [-1,-08], [0.2, 0.4] и [0.6, 0.8]. Это означает, что на каждом из них имеется корень данного полинома. И, как видно из графика, эти корни приблизительно равны x0=-0.9, x1=0.2 и x3=0.7, соответственно.
Уточним значения корней, используя встроенную в MS Excel процедуру Подбор параметра.
Предварительно построим отдельную таблицу для уточнения значения корней (рис.4, табл. 2).
В клетку E9 введем приближенное значение 1-го корня -0,9. В клетку F9 введём формулу = E9^3-0,01*E9^2-0,7044*E9+0,139104
Выполним команду:
Данные, Анализ «что-если», Подбор параметра, Установить в ячейке: F9, Значение: 0, Изменяя значение ячейки: $E$9, Ok.
В диалоговом окне Подбора параметра просматриваем значение полинома при найденном значении корня и нажимаем Ok.
Найденное значение корня, MS Excel помещает в клетку E9.
Аналогично рассмотренному можно уточнить взятые из графика значения других корней уравнения. В качестве начальных значений корней в клетках e10 и e11 занесём, взятые из графика, грубые значения х=0,3 и х=0,7
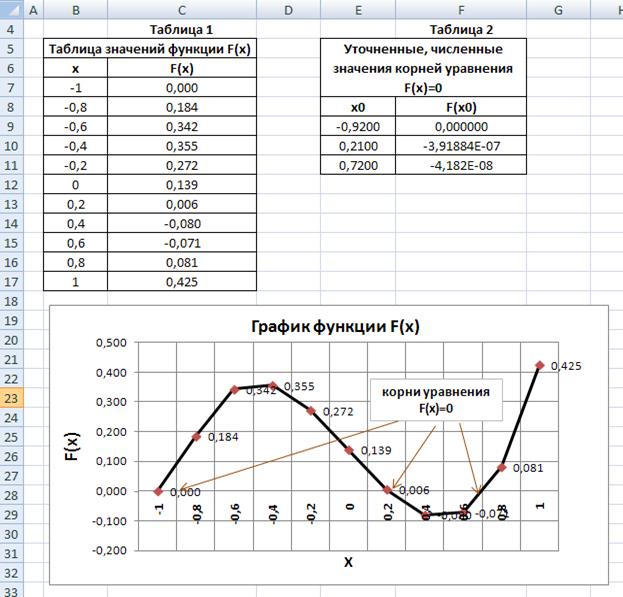
Рис. 4. Локализация и уточнение значений корней нелинейного уравнения F(x)=0
Индивидуальные задания к работе 3.3 (табл. 3).
Порядок выполнения задания.
1. Построив график функции f(x) в заданном интервале x=[a,b] расположения корней уравнения f(x) = 0, определите приближённые (взятые по графику) их значения;
2. Используя процедуру Подбора параметра, найдите более точные численные значения корней, при которых значение функции f(x) не превышает заданной абсолютной погрешности вычислений |eps(f(x))|=0,0001. Индивидуальное задание должно быть выполнено на отдельном листе Лаб3.3 файла Лаб3.xls
Примечание. Все материалы выполненной работы (условие задания, таблицы и диаграммы) должны быть размещены в пределах 1-го окна дисплея и таким образом, чтобы их можно было распечатать на одном листе книжного формата А 4.
Таблица 3 – Варианты заданий к лабораторной работе 3.3
| # | f(x) | f(x) | |
| +1 | 
| +16 | 
|
| +2 | 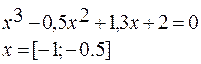
| 
| |
| +3 | 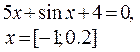
| +18 | 
|
| +4 | 
| +19 | 
|

| +20 | 
| |
| +6 | 
| +21 | 
|

| 
| ||
| +8 | 
| +23 | 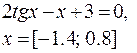
|
| +9 | 
| +24 | 
|
| +10 | 
| +25 | 
|

| +26 | 
| |
| +12 | 
| +27 | 
|
| +13 | 
| +28 | 
|
| +14 | 
| 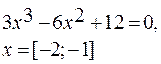
| |
| +15 | 
| 
| |
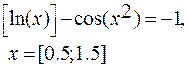
| 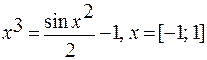
| ||

| 
|
Работа 3.4.






