Две плоскости пересекаются между собой по прямой линии. Если две плоскости заданы следами на плоскостях проекций, то точки, определяющие линию пересечения этих плоскостей, следует искать в точках пересечения одноименных следов заданных плоскостей. Прямую, проходящую через эти точки, можно считать принадлежащей каждой из рассматриваемых пересекающихся плоскостей.
Для построения линии пересечения плоскостей Р и Q необходимо:
1. Найти точку пересечения фронтальных следов.
2. Найти точку пересечения горизонтальных следов.
3. Построить проекции полученных точек.
4. Построить фронтальную и горизонтальную проекцию линии пересечения плоскостей.
Плоскость Р задана тремя точками: точкой схода следов Р12 , точкой А, лежащей на следе f2, точкой В, лежащей на следе h1. Плоскость Q также задана тремя точками: точкой схода следов Q12, точкой С, лежащей на следе f2¢, точкой D, лежащей на следе h1¢. Данные для построения находятся в таблице 3. Графические условия даны на рис 3.
Таблица 3
| № вари-анта | Плоскость Р | Плоскость Q | ||||||||
| Xa | Za | P12 | Xв | Yв | Xc | Zc | Q12 | Xd | Yd | |
 Задача 4. Определение точки пересечения прямой общего положения АВ с плоскостью общего положения Р, заданной следами.
Задача 4. Определение точки пересечения прямой общего положения АВ с плоскостью общего положения Р, заданной следами.
Пояснения к решению задачи 4. Для решения задачи необходимо:
1. Заключить заданную прямую в проецирующую плоскость. В качестве проецирующей может быть выбрана фронтально-проецирующая или горизонтально-проецирующая плоскости в зависимости от конкретного графического условия задачи.
2. Построить линию пересечения выбранной проецирующей плоскости с заданной плоскостью.
3. Найти точку пересечения построенной линии пересечения и заданной прямой. Это и будет искомая точка пересечения прямой с плоскостью.
Плоскость общего положения Р задана тремя точками: точкой схода следов Р12, точкой С, лежащей на следе f2 и точкой D, лежащей на следе h1. Прямая АВ задана двумя точками. Данные для построения находятся в таблице 4. Графические условия даны на рис 4.
Таблица 4
| № вари-анта | Плоскость Р | Прямая АВ | ||||||||||||||
| С | Р12 | D | A | B | ||||||||||||
| Xc | Zc | Xp | Xd | Yd | Xa | Ya | Za | Xb | Yb | Zb | ||||||
 Задача 5. Определение истинной величины треугольника KPD способом замены плоскостей проекций.
Задача 5. Определение истинной величины треугольника KPD способом замены плоскостей проекций.
Пояснения к решению задачи 5. Треугольник KPD задан координатами вершин К(Xк, Yк, Zк),
Р (Xp, Yp, Zp), D (Xd, Yd, Zd). Для решения данной задачи по определению истинной величины треугольника KPD необходима двойная замена плоскостейпроекций.
В результате первой замены плоскостейпроекций плоскость треугольника KPD необходимо поставить в положение проецирующей плоскости. Для этого новую дополнительную плоскость проекций П4 необходимо провести перпендикулярно любой горизонтали плоскости треугольника КРD. Для уменьшения количества построений проводится горизонталь DE через вершину треугольника KPD. В этом случае треугольник KPD на плоскости П4 изобразится в виде прямой линии.
Вторую замену плоскостей проекций осуществим, проведя новую плоскость проекций П5, параллельно плоскости треугольника К Р D. Данные для построения находятся в таблице 5. Графические условия даны на рис 5.
Таблица 5
| № вари-анта | Координаты | ||||||||
| К | Р | D | |||||||
| Хk | Yk | Zk | Хр | Yp | Zp | Xd | Yd | Zd | |
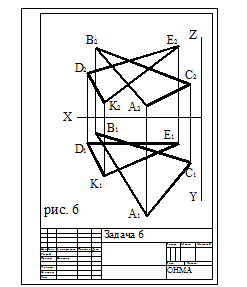 Задача 6. Построение линии пересечения треугольников АВС и EDK.
Задача 6. Построение линии пересечения треугольников АВС и EDK.
Пояснения к решению задачи 6. На формате намечаются оси координат и из табл. 6 согласно своему варианту берутся координаты точек А, В, С, D, Е, К вершин треугольника. Линия пересечения треугольников строится по точкам пересечения сторон одного треугольника с другим треугольником.
Видимость сторон треугольников определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными жирными линиями, невидимые следует показать штриховыми линиями. Данные для построения находятся в таблице 6. Графические условия даны на рис 6.
Таблица 6
| № вари-анта | Координаты | |||||||||||||||||
| Xа | Ya | Za | Хb | Yb | Zb | Хс | Yc | Zc | Хd | Yd | Zd | Xе | Ye | Ze | Хk | Yk | Zk | |
 Задача 7. Построение проекции пирамиды, основанием которой является треугольник АВС, а ребро SA определяет высоту h пирамиды.
Задача 7. Построение проекции пирамиды, основанием которой является треугольник АВС, а ребро SA определяет высоту h пирамиды.






