И конденсатора
Когда к цепи (рис. 4.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.

Рис. 4.1
Общий ток цепи I разветвляется на ток в конденсаторе IC (емкостная составляющая общего тока) и ток в резисторе IC (активная составляющая).
Между токами I, IC и IR существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением Хс конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 4.2).
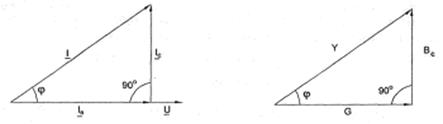
Рис. 4.2 Рис. 4.3
Фазовый сдвиг между напряжением U цепи и током в резисторе IR отсутствует, тогда как между этим напряжением и током в конденсаторе IC равен -90° (т.е. ток опережает напряжение на 90). При этом сдвиг между полным током I и напряжением U цепи определяется соотношением между проводимостями ВC и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 4.3).
В треугольнике проводимостей G=l/R, Вс=1/Хс, a Y представляет собой так называемую полную проводимость цепи в См, тогда как G - активная, а ВC -реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:  .
.
Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи:
 |
Полная проводимость цепи:
 ;
; 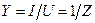 ,
,
где Z - полное сопротивление цепи;
Угол сдвига фаз:

Активная и реактивная проводимости:


Экспериментальная часть
Задание
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IR и конденсаторе IC, полный ток I и вычислите угол сдвига фаз, полное сопротивление цепи Z и емкостную реактивную проводимость ВC.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 4.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.

Рис. 4.4
· Выполните измерения U, I, IC, IR и занесите результаты в таблицу 4.1
Таблица 4.1
| U, в | I, мА | I C, мА | IR, мА | φ. град | R, Ом | ХC, Ом | Z, Ом | Примечание |
| Расчет |
· Вычислите и запишите в таблицу:
Фазовый угол
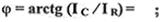
Активные проводимость цепи и сопротивление цепи
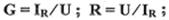
Емкостные реактивные проводимость и сопротивление цепи
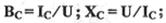
Полные проводимость и сопротивление цепи

· Сравните результаты вычислений с результатами виртуальных измерений (если они есть).
· Постройте векторную диаграмму токов (рис. 4.5) и треугольник проводимостей (рис.4.6).

Рис. 4.5 Рис. 4.6
Контрольные вопросы:
- Дать определения полной, активной, емкостной проводимостей.
- Дать физическое толкование угла сдвига фаз между током и напряжением
- Какой вид имеет временная диаграмма напряжений и тока при параллельном соединении R и C-цепей?
- Начертите векторные диаграммы для разветвленной цепи с активно-индуктивной нагрузкой.
- Как рассчитать проводимости для параллельного соединения резистора и идеального конденсатора?
- Пояснить, что такое R,X,Z,G,B,Y. Какие соотношения связывают их между собой?
- Как определить ток в неразветвленной части цепи переменного тока, если известны токи в параллельных ветвях?
- Как изменится активная мощность исследуемой цепи при изменении емкости?
Лабораторная работа 5






