ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
КИНЕМАТИКА
1. Определить модуль скорости материальной точки в момент времени  с, если точка движется по закону
с, если точка движется по закону 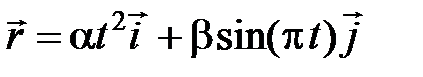 , где
, где  м/с2;
м/с2;  м.
м.
2. Материальная точка движется по закону  , где
, где  м;
м;  м. Определить вектор скорости, вектор ускорения и траекторию движения материальной точки.
м. Определить вектор скорости, вектор ускорения и траекторию движения материальной точки.
3. Радиус-вектор частицы изменяется со временем по закону:  (м). Найти: а) скорость
(м). Найти: а) скорость  и ускорение
и ускорение  частицы; б) модуль скорости
частицы; б) модуль скорости  в момент
в момент  с; в) приближенное значение пути S, пройденного частицей за 11-ю секунду движения.
с; в) приближенное значение пути S, пройденного частицей за 11-ю секунду движения.
4. Частица движется со скоростью  , где
, где  м/с2. Найти:
м/с2. Найти:
а) модуль скорости  частицы в момент времени
частицы в момент времени  с; б) ускорение частицы
с; б) ускорение частицы  и его модуль; в) путь S, пройденный частицей с момента
и его модуль; в) путь S, пройденный частицей с момента  с до момента
с до момента  с.
с.
5. Зависимость пройденного телом пути от времени задается уравнением S =A+Bt+Ct 2 +Dt 3(С =0,1 м/с2, D =0,03 м/с3). Определить: 1) время после начала движения, через которое ускорение а тела будет равно 2 м/с2; 2) среднее ускорение á а ñ тела за этот промежуток времени.
6. Тело брошено с высоты 25 м вертикально вверх со скоростью 20 м/с. Найти путь и среднюю скорость движения тела (до момента падения).
7. Звук выстрела и пуля одновременно достигают высоты 990 м. Выстрел произведён вертикально вверх. Определить начальную скорость пули. Средняя скорость звука в воздухе 330 м /с.
8. Вертолёт летит горизонтально со скоростью 40 м/с на высоте 45 м. С вертолета нужно сбросить груз на баржу, движущуюся в том же направлении со скоростью 2 м/с. На каком расстоянии, не долетев до баржи, летчик должен освободить крепеж груза?
9. Тело брошено вертикально вверх с начальной скоростью v0=4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью v0 вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
10. Материальная точка движется прямолинейно с ускорением а =5 м/с2. Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять v 0=0.
11. Две автомашины движутся по дорогам, угол между которыми α=60°. Скорости автомашин v1=54 км/ч и v2=72км/ч. С какой скоростью v удаляются машины одна от другой?
12. Скорость течения реки  , а скорость движения лодки относительно воды
, а скорость движения лодки относительно воды  . Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.
. Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.
13. Два электропоезда проследовали со скоростью 60 км/ч мимо одной платформы в одном направлении с интервалом в 20 мин. С каким интервалом по времени их встретит поезд, идущий по встречной колее, если его скорость 72 км/ч?
14. Пловец переплывает реку по прямой, перпендикулярной берегу. Во сколько раз скорость пловца относительно воды больше скорости течения реки, если угол между векторами скорости пловца относительно воды и относительно берега равен 45°.
15. Материальная точка движется прямолинейно с начальной скоростью v 0=10 м/с и постоянным ускорением а =-5м/с2. Определить, во сколько раз путь Δs, пройденный материальной точкой, будет превышать модуль ее перемещения Δr спустя t=4c после начала отсчета времени.
16. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью v1=18 км/ч. Далее половину оставшегося времени он ехал со скоростью v2=22 км/ч, после чего до конечного пункта он шел пешком со скоростью v3=5 км/ч. Определить среднюю скорость <v> велосипедиста.
17. Камень, брошенный по льду со скоростью  м/с, останавливается на расстоянии
м/с, останавливается на расстоянии  м от места бросания. Определить путь, пройденный камнем за первые
м от места бросания. Определить путь, пройденный камнем за первые  с движения.
с движения.
18. Тело падает с высоты  км с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определите, какое время понадобится телу для прохождения: 1) первых 10 м пути; 2) последних 10 м пути.
км с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определите, какое время понадобится телу для прохождения: 1) первых 10 м пути; 2) последних 10 м пути.
19. Тело, брошенное вертикально вверх, находилось на одной и той же высоте  м два раза с интервалом
м два раза с интервалом  с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.
с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.
20. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета.
21. С башни высотой 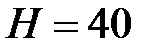 м брошено тело со скоростью
м брошено тело со скоростью  м/с под углом
м/с под углом  к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) время движения тела; 2) на каком расстоянии от основания башни тело упадет на землю; 3) скорость падения тела на землю; 4) угол, который составит траектория тела с горизонтом в точке его падения.
к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) время движения тела; 2) на каком расстоянии от основания башни тело упадет на землю; 3) скорость падения тела на землю; 4) угол, который составит траектория тела с горизонтом в точке его падения.
22. Мяч брошен с поверхности Земли со скоростью  м/с под углом
м/с под углом  к горизонту. Определить радиус кривизны его траектории в верхней точке подъема
к горизонту. Определить радиус кривизны его траектории в верхней точке подъема  и в момент падения на Землю
и в момент падения на Землю 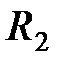 .
.
23. Тело брошено под углом α=30° к горизонту со скоростью v0=30 м/с. Каковы будут нормальное аn и тангенциальное аτ ускорения тела через время t=1с после начала движения?
24. Из пушки выпустили последовательно два снаряда со скоростью  м/с: первый под углом
м/с: первый под углом  ° к горизонту, второй – под углом
° к горизонту, второй – под углом  ° (азимут один и тот же). Найти интервал времени между снарядами, при котором снаряды столкнутся друг с другом.
° (азимут один и тот же). Найти интервал времени между снарядами, при котором снаряды столкнутся друг с другом.
25. Под каким углом к горизонту надо бросить шарик, чтобы радиус кривизны в начале его траектории был в h = 8,0 раз больше, чем в вершине?
26. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Уравнение движения автомобиля 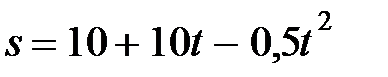 (м). Найти скорость автомобиля, а также его тангенциальное, нормальное и полное ускорение в момент времени
(м). Найти скорость автомобиля, а также его тангенциальное, нормальное и полное ускорение в момент времени 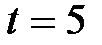 с.
с.
27. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние между которыми 30 м. Пробоина во втором листе оказалась на 10 см ниже, чем в первом. Определить скорость пули, если к первому листу она подлетела, двигаясь горизонтально.
28. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара мяча о стенку на 1 м меньше высоты, с которой был брошен мяч. С какой скоростью был брошен мяч? Под каким углом он подлетел к поверхности стенки?
29. Два тела брошены одновременно из одной точки: одно – вертикально вверх, другое – под углом  ° к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7с.
° к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7с.
30. Колесо вращается с постоянной скоростью, соответствующей 100об/мин. С некоторого момента колесо тормозится и вращается равнозамедленно с угловым ускорением 3 рад/с2. Через какое время колесо остановится?
31. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали груз и предоставили ему возможность опускаться. Двигаясь равноускоренно, груз за время t = 3с опустился на  = 1,5 м. Определить угловое ускорение e цилиндра, если его радиус R = 4 см.
= 1,5 м. Определить угловое ускорение e цилиндра, если его радиус R = 4 см.
32. Минутная стрелка часов в 3 раза длиннее секундной. Найти соотношение между линейными скоростями концов этих стрелок.
33. Колесо радиусом R =0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением w = 2 At + 5 Bt 4(A = 2 рад/с2 и B = 1 рад/с5). Определить полное ускорение точек обода колеса через t =1 с после начала вращения и число оборотов, сделанных колесом за это время.
34. Нормальное ускорение точки, движущейся по окружности радиусом r =4 м, задается уравнением an=A+Bt+Ct 2(А= 1 м/с2, B =6 м/с3, С =3 м/с4). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t 1= 5 с после начала движения; 3) полное ускорение для момента времени t 2=1 с.
35. Частота вращения колеса при равнозамедленном движении за t =1 мин уменьшилась от 300 до 180 мин–1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
36. Диск радиусом R =10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением j= A+Bt+Ct 2 +Dt 3 (B =1 рад/с, С =1 рад/с2, D =1 рад/с3). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение 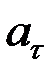 ; 2) нормальное ускорение аn; 3) полное ускорение а.
; 2) нормальное ускорение аn; 3) полное ускорение а.
37. Материальная точка движется по окружности с постоянной угловой скоростью ω=π/6 рад/с. Во сколько раз путь Δs, пройденный точкой за время t=4 с, будет больше модуля ее перемещения Δr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол φ0=π/3 рад.
38. Материальная точка движется в плоскости ху согласно уравнениям  и
и  , где
, где 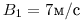 ,
, 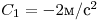 , B2= – 1м/с, С2 =0,2 м/с2. Найти модули скорости и ускорения точки в момент времени
, B2= – 1м/с, С2 =0,2 м/с2. Найти модули скорости и ускорения точки в момент времени  .
.
39. По краю равномерно вращающейся с угловой скоростью w =1 рад/с платформы идет человек и обходит платформу за время t=9,9 с. Каково наибольшее ускорение а движения человека относительно Земли. Принять радиус платформы R=2м.
40. Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением. Определить тангенциальное ускорение а точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение аn=2,7 м/с2.
ДИНАМИКА
41. Ледяная горка составляет с горизонтом угол  . По ней снизу вверх толкнули санки, которые, поднявшись на некоторую высоту, затем соскальзывают вниз по потому же пути. Определить коэффициент трения, если время спуска в
. По ней снизу вверх толкнули санки, которые, поднявшись на некоторую высоту, затем соскальзывают вниз по потому же пути. Определить коэффициент трения, если время спуска в  раза больше времени подъема.
раза больше времени подъема.
42. Тело массой 10 кг тянут по горизонтальной поверхности с силой 40 Н. Если эта сила приложена к телу под углом 60° к горизонту, оно двигается равномерно. С каким ускорением будет двигаться тело, если силу приложить под углом 30°?
43. Шайбу положили на наклонную плоскость и сообщили ей направленную вверх вдоль плоскости начальную скорость  . Коэффициент трения между шайбой и плоскостью равен m. При каком значении угла наклона a шайба пройдет вверх по плоскости наименьшее расстояние? Чему оно равно?
. Коэффициент трения между шайбой и плоскостью равен m. При каком значении угла наклона a шайба пройдет вверх по плоскости наименьшее расстояние? Чему оно равно?
44. К концам нити, перекинутой через блок, прикреплены грузы, массы которых  кг и
кг и  кг. Первоначально грузы находились на одном уровне. Определить, на какое расстояние S по вертикали разойдутся грузы через
кг. Первоначально грузы находились на одном уровне. Определить, на какое расстояние S по вертикали разойдутся грузы через 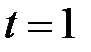 с после начала движения. Найти силу натяжения нити T.
с после начала движения. Найти силу натяжения нити T.
45. Человек, масса которого  кг, стоит на корме лодки, находящейся на озере. Длина лодки
кг, стоит на корме лодки, находящейся на озере. Длина лодки  м, ее масса
м, ее масса  кг. Человек переходит на нос лодки. На какое расстояние передвинется человек относительно дна озера? Сопротивлением воды пренебречь.
кг. Человек переходит на нос лодки. На какое расстояние передвинется человек относительно дна озера? Сопротивлением воды пренебречь.
46. Тепловоз (масса  т) равномерно поднимается в гору с уклоном
т) равномерно поднимается в гору с уклоном  . Коэффициент трения
. Коэффициент трения  . Определить развиваемую тепловозом мощность при скорости движения
. Определить развиваемую тепловозом мощность при скорости движения  км/ч.
км/ч.
47. Какой путь до остановки пройдут санки по горизонтальной поверхности после спуска, с начальной скоростью, равной нулю с горы высотой  м, имеющей уклон
м, имеющей уклон  ? Коэффициент трения скольжения
? Коэффициент трения скольжения  .
.
48. Два соприкасающихся шара висят на нитях одинаковой длины. Первый шар отводят в сторону и отпускают. После упругого удара шары поднимаются на одну и туже высоту. Найти массу первого шара  , если масса второго шара
, если масса второго шара  кг.
кг.
49. Мотоциклист движется со скоростью  м/с по окружности радиусом
м/с по окружности радиусом  м. На какой угол
м. На какой угол  от вертикали он должен наклониться, чтобы сохранить равновесие?
от вертикали он должен наклониться, чтобы сохранить равновесие?
50. Тело, начальная скорость которого  м/с, движется прямолинейно с ускорением
м/с, движется прямолинейно с ускорением  м/с2. Во сколько раз изменится импульс тела при прохождении им пути
м/с2. Во сколько раз изменится импульс тела при прохождении им пути  м?
м?
51. Два тела (их массы  кг и
кг и  кг) движутся равномерно во взаимно перпендикулярных направлениях. Скорость первого тела
кг) движутся равномерно во взаимно перпендикулярных направлениях. Скорость первого тела  м/с, а второго
м/с, а второго  м/с. Определить импульс данной системы тел.
м/с. Определить импульс данной системы тел.
52. Материальная точка, масса которой  кг, двигаясь равномерно по окружности, описывает четверть окружности радиусом
кг, двигаясь равномерно по окружности, описывает четверть окружности радиусом  м в течении
м в течении  c. Найти модуль изменения импульса материальной точки за это время.
c. Найти модуль изменения импульса материальной точки за это время.
53. Стрела, летящая со скоростью 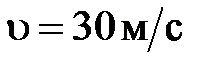 , попадает в мишень и останавливается за время
, попадает в мишень и останавливается за время  c. Масса стрелы
c. Масса стрелы  кг. Определить величину силы сопротивления
кг. Определить величину силы сопротивления  , предполагая, что она постоянна в интервале
, предполагая, что она постоянна в интервале  .
.
54. При горизонтальном полете со скоростью V=250 м/с снаряд массой M =8кг разорвался на две части. Большая часть массой m1=6 кг получила скорость V1=400 м/с в направлении полета снаряда. Определить модуль и направление скорости V2 меньшей части снаряда.
55. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α=30° к линии горизонта. Определить скорость V2 отката платформы, если снаряд вылетает со скоростью V1=480 м/с. Масса платформы с орудием и снарядами M=18т, масса снаряда m =60 кг.
56. Человек массой m=70 кг, бегущий со скоростью V1=9 км/ч, догоняет тележку массой M=190кг, движущуюся со скоростью V2=3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
57. Конькобежец, стоя на коньках на льду, бросает камень массой m=2,5 кг под углом α=30° к горизонту со скоростью V1=10м/с. Какова будет начальная скорость V2 движения конькобежца, если масса его M=60 кг? Перемещением конькобежца во время броска пренебречь.
58. Снаряд, летевший со скоростью V=400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью V2=150 м/с. Определить скорость V1 большего осколка.
59. В подвешенный на нити длиной L=1,8 м деревянный шар массой m2 =0,8 кг попадает горизонтально летящая пуля массой m1= 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α=30°? Размером шара пренебречь. Удар считать прямым, центральным.
60. Шар массой m=1 кг движется со скоростью V0=4 м/с и сталкивается с шаром массой M=2 кг, движущимся навстречу ему со скоростью V=3 м/с. Каковы скорости V1 и V2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
61. Шар массой m=3 кг движется со скоростью V0=2 м/с и сталкивается с покоящимся шаром массой M=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
62. Шар массой m=2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу M большего шара. Удар считать абсолютно упругим, прямым, центральным.
63. Определить работу растяжения двух соединенных последовательно пружин жесткостями k1=400 Н/м и k2=250 Н/м, если первая пружина при этом растянулась на x1= 2 см.
64. Из шахты глубиной H=600 м поднимают клеть массой m1=3,0 т на канате, каждый метр которого имеет массу m2= 1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия подъемного устройства
65. Пружина жесткостью 500 Н/м сжата силой 100 Н. Определить работу внешней силы, дополнительно сжимающей эту, пружину еще на 2 см.
66. Две пружины жесткостью k1=0,5 кН/м и k2=1кН/м скреплены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации x=4 см.
67. Какую нужно совершить работу А, чтобы пружину жесткостью k=800 Н/м, сжатую на x1=6 см, дополнительно сжать на x= 8 см?
68. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на l =3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h=8 см?
69. Из пружинного пистолета с пружиной жесткостью k= 150 Н/м был произведен выстрел пулей массой m= 8 г. Определить скорость V пули при вылете ее из пистолета, если пружина была сжата на x=4 см.
70. Налетев на пружинный буфер, вагон массой m=16 т, двигавшийся со скоростью V= 0,6 м/с, остановился, сжав пружину на x= 8 см. Найти общую жесткость k пружин буфера.
71. Шарик массой m=60 г, привязанный к концу нити длиной L 1=l,2 м, вращается с частотой ν 1=2с-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния L 2=0,6 м. С какой частотой ν 2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
72. По касательной к шкиву маховика в виде диска диаметром D=75 см и массой m=40 кг приложена сила F=1 кН. Определить угловое ускорение и частоту вращения маховика через время t= 10 с после начала действия силы, если радиус R шкива равен 12 см. Силой трения пренебречь.
73. На обод маховика диаметром D=60 см намотан шнур, к концу которого привязан груз массой m=2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t=3 с приобрел угловую скорость w=9 рад/с.
74. Нить с привязанными к ее концам грузами массами m1=50 г и m2= 60 г перекинута через блок диаметром D=4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε=1,5 рад/с2. Трением и проскальзыванием нити по блоку пренебречь.
75. Определить момент силы N, который необходимо приложить к блоку, вращающемуся с частотой ν=12с-1, чтобы он остановился в течение времени t=8 с. Диаметр блока D=30 см. Массу блока m=6 кг считать равномерно распределенной по ободу.
76. К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой подвешены грузы. Один груз движется по поверхности стола, а другой вдоль вертикали вниз. Определить коэффициент трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением а =0,56м/с2. Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.
77. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой m=5 кг каждая. Расстояние от каждой гири до оси скамьи L1=70 см. Скамья вращается с частотой ν=1с-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до L2=20 см? Момент инерции человека и скамьи (вместе) относительно оси J=2,5 кг м2.
78. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью w1=4 рад/с. С какой угловой скоростью w2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J=5 кг м2. Длина стержня L=1,8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
79. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой w1=8 мин-1, стоит человек массой m=70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой w2=10 мин-1. Определить массу M платформы. Момент инерции человека рассчитывать как для материальной точки.
80. Однородный стержень длиной L=1,0 м и массой m2=0,7 кг подвешен на горизонтальной оси, проходящей через верхний конец стержня. В точку, отстоящую от оси на 2/3L, абсолютно упруго ударяет пуля массой m1=5 г, летящая перпендикулярно стержню и его оси. После удара стержень отклонился на угол α=60°. Определить скорость пули.
ГРАВИТАЦИЯ. РЕЛЯТИВИСТСКАЯ МЕХАНИКА. МЕХАНИКА ЖИДКОСТИ
81. С поверхности Земли вертикально вверх пущена ракета со скоростью V=5 км/с. На какую высоту она поднимется?
82. По круговой орбите вокруг Земли обращается спутник с периодом T=90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус RЗ считать известными.
83. Спутник обращается вокруг Земли по круговой орбите на высоте r =520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус RЗ считать известными.
84. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте r =1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус RЗ считать известными.
85. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84 108 м?
86. Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус RЗ Земли в 3,90 раз больше радиуса RЛ Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.
87. Плотность вещества некоторой шарообразной планеты составляет 3 г/см3. Каким должен быть период обращения планеты вокруг собственной оси, чтобы на экваторе тела были невесомыми?
88. Стержень движется в продольном направлении с постоянной скоростью  относительно инерциальной К- системы отсчета. При каком значении
относительно инерциальной К- системы отсчета. При каком значении  длина стержня в этой системе отсчета будет на
длина стержня в этой системе отсчета будет на  = 0,5 % меньше его собственной длины?
= 0,5 % меньше его собственной длины?
89. Имеется треугольник, собственная длина каждой стороны которого равна а. Найти периметр этого треугольника в системе отсчета, движущейся относительно него с постоянной скоростью  вдоль одной из его биссектрис. Исследовать полученный результат при
вдоль одной из его биссектрис. Исследовать полученный результат при  << c и
<< c и  < (~) c, где с – скорость света.
< (~) c, где с – скорость света.
90. Имеется треугольник, собственная длина каждой стороны которого равна а. Найти периметр этого треугольника в системе отсчета, движущейся относительно него с постоянной скоростью  вдоль одной из его сторон. Исследовать полученный результат при
вдоль одной из его сторон. Исследовать полученный результат при  << c и
<< c и  < (~) c, где с – скорость света.
< (~) c, где с – скорость света.
91. Собственное время жизни некоторой нестабильной частицы  нc. Найти путь, который пролетит эта частица до распада в лабораторной системе отсчета, где ее время жизни Δ t = 20 нc.
нc. Найти путь, который пролетит эта частица до распада в лабораторной системе отсчета, где ее время жизни Δ t = 20 нc.
92. В К -системе отсчета мю-мезон, движущийся со скоростью  , пролетел от места своего рождения до точки распада расстояние
, пролетел от места своего рождения до точки распада расстояние  = 3,0 км. Определить: а) собственное время жизни этого мезона; б) расстояние, которое пролетел мезон в К -системе с «его точки зрения».
= 3,0 км. Определить: а) собственное время жизни этого мезона; б) расстояние, которое пролетел мезон в К -системе с «его точки зрения».
93. Космический корабль движется со скоростью  с по направлению к Земле. Определите расстояние, пройденное им в системе отчета, связанной с Землей, за
с по направлению к Земле. Определите расстояние, пройденное им в системе отчета, связанной с Землей, за  c, отсчитанное по часам в космическом корабле.
c, отсчитанное по часам в космическом корабле.
94. Космический корабль удаляется от Земли с относительной скоростью  , с него стартует ракета (в направлении от Земли) со скоростью
, с него стартует ракета (в направлении от Земли) со скоростью  относительно корабля. Определите скорость ракеты относительно Земли.
относительно корабля. Определите скорость ракеты относительно Земли.
95. Определите, на, сколько процентов полная энергия релятивистской элементарной частицы, вылетающей из ускорителя со скоростью  с, больше ее энергии покоя.
с, больше ее энергии покоя.
96. Во сколько раз релятивистская масса частицы, скорость которой отличается от скорости света на 0,010 %, превышает ее массу покоя?
97. Найти скорость, при которой релятивистский импульс частицы в 2 раза превышает ее ньютоновский импульс.
98. Какую работу необходимо совершить, чтобы увеличить скорость частицы с массой покоя m 0 от 0,60 с до 0,80 с? Сравнить полученный результат со значением, вычисленным по классической формуле.
99. Найти скорость, при которой кинетическая энергия частицы равна ее энергии покоя.
100. Найти зависимость импульса от кинетической энергии частицы с массой покоя т 0. Вычислить импульс протона с кинетической энергией 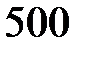 МэВ.
МэВ.
101. Электрон летит со скоростью, составляющей 80% от скорости света в вакууме. Определить кинетическую энергию электрона в мегаэлектрон – вольтах.
102. Циклотрон дает пучок электронов с кинетической энергией 0,67 МэВ. Какую долю скорости света составляет скорость электронов в этом пучке?
103. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Во сколько раз сила трения, действующая на всплывающий шарик, больше силы тяжести, действующей на этот шарик?
104. Найти скорость течения углекислого газа по трубе, если известно, что за время 30 мин через поперечное сечение трубы протекает масса газа 0,51 кг. Плотность газа 7,5 кг/м3. Диаметр трубы 2 см.
105. Пенопластовый шарик, погруженный под воду на глубину 120 см, всплывает на поверхность за 0,4 с. Сила сопротивления воды 2,5 Н. Определить объем шарика. Плотность пенопласта 200 кг/м3, плотность воды 1000 кг/м3.
106. Какое давление создается в краскопульте, если струя жидкой краски выбрасывается из него со скоростью 10 м/с? Плотность краски 0,8 г/см3.
107. Какой наибольшей скорости может достичь дождевая капля диаметром 1 мм? Динамическая вязкость воздуха h = 1,2×10–5 кг/(м×с).
108. Пробковый шарик с плотностью rп, диаметром D всплывает в вязкой жидкости с плотностью rж с постоянной скоростью u. Определить вязкость жидкости.
109. Полый железный шар (r = 7,87 г/см3) весит в воздухе 5 Н, а в воде (r ' = 1 г/см3) — 3 Н. Пренебрегая выталкивающей силой воздуха, определить объем внутренней полости шара.
110. Аэростат, наполненный водородом, поднимается с ускорением 1 м/с2. Масса оболочки аэростата с грузом 700 кг. Плотность воздуха 1, 29 кг/м3. Определить объем аэростата.
111. В широком сосуде, наполненном глицерином (плотность r =1,2 г/см3), падает с установившейся скоростью 5 см/с стеклянный шарик (r' = 2,7 г/см3) диаметром 1 мм. Определить динамическую вязкость глицерина.
112. К пробковому поплавку массой 1 кг привязан на нити свинцовый груз так, что поплавок полностью погружен в воду. Определить массу груза и силу упругости нити, если плотность пробки 200 кг/м3.
113. Шарик массой 8 г опускают в воду на глубину 30 см и отпускают. В результате он выпрыгивает из воды на высоту 120 см. Определить плотность шарика и его диаметр, если сила сопротивления воды составляет 10 % от силы тяжести шарика.
114. Тонкая палочка шарнирно закреплена одним концом и опущена свободным концом в воду. Определить плотность палочки, если равновесие достигается, когда в воду погружена половина палочки.
115. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость течения в широкой части трубы 20 см/с. Определить скорость течения в узкой части трубы, диаметр которой в 1.5 раза меньше диаметра широкой части.
116. На рычаге уравновешены два тела одинакового объема из разного материала. Нарушится ли равновесие рычага, если тела погрузить в воду?
117. На рычаге уравновешены два тела одинаковой массы из разного материала. Нарушится ли равновесие рычага, если тела погрузить в воду?
118. На рычаге уравновешены два тела из одного и того же материала разной массы. Нарушится ли равновесие рычага, если тела погрузить в воду?
119. К поршню спринцовки, расположенной горизонтально, приложена сила 15 Н. Определить скорость истечения воды из наконечника спринцовки, если площадь поршня 12 см2.
120. В широкой части горизонтально расположенной трубы нефть течет со скоростью 2 м/с. Определить скорость течения нефти в узкой части трубы, если разность давлений в широкой и узкой частях трубы 50 мм рт.ст.






