Лабораторная работа № 4. Переходные процессы в цепях первого и второго порядка
Цель работы: получение навыков экспериментального исследования переходных процессов в цепи с одним накопителем энергии (конденсатором) и с двумя накопителями энергии.
Подготовка к работе:
Что такое переходные процессы и в результате чего они возникают? В каких цепях имеют место переходные процессы?
Переходные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.
2) Записать законы коммутации.
Ток через индуктивный элемент L непосредственно до коммутации iL (0-) равен току во время коммутации и току через этот же индуктивный элемент непосредственно после коммутации iL (0+), так как ток в катушке мгновенно измениться не может:
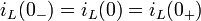
Напряжение на конденсаторе С непосредственно до коммутации UC (0-) равно напряжению во время коммутации и напряжению на конденсаторе непосредственно после коммутации UC (0+), так как невозможен скачок напряжения на конденсаторе:
3) Что такое переходный, принуждённый и свободный токи?
Переходный ток - процесс перехода электрического тока из одного состояния в другое (включение, выключение, переключение, изменение параметров элементов цепи и др.)
Принужденный ток - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону
Свободный ток - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.
4) Каков физический смысл постоянной времени цепи? Чему равна постоянная времени цепи R-C?
Постоянная времени цепи – это время за которое свободная составляющая напряжением или тока изменится в «е» раз.
5) Что называют коэффициентом затухания цепи?
6) Привести уравнения, по которым изменяются uC(t), iC(t) при коротком замыкании цепи R-C, начертить графики uC(t), iC(t).
7) Записать уравнение по второму закону Кирхгофа для свободных составляющих напряжений цепи R-L-C и соответствующее ему характеристическое уравнение.
По второму закону Кирхгофа t ≥ 0 имеем:
.
Учитывая, что 
, получаем дифференциальное уравнение второго порядка для свободной составляющей напряжения
.
Характеристическое уравнение при этом имеет вид:
.
Характер электромагнитных процессов в контуре зависит от соотношения параметров R, L, С, входящих в выражение для корней характеристического уравнения
.
В зависимости от знака подкоренного выражения корни могут быть вещественными или комплексно-сопряженными. Они определяют характер свободных составляющих переходных токов и напряжений.
8) При каких корнях характеристического уравнения в цепи R-L-C возникает апериодический разряд конденсатора? Написать уравнения для uC(t), i(t), uL(t) при апериодическом разряде конденсатора. Привести графики этих величин.
Пусть корни характеристического уравнения вещественны и отличны друг от друга. Это имеет место при условии
.
Так как 
и 
и, кроме того, 
, то при изменении t от 0 до ∞ величины 
и 
убывают от 1 до 0 и при том разность 
всегда положительна.
Ток i не меняет своего направления, т.е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называют апериодическим.
В интервале времени 0 < t < tm ток по абсолютному значению возрастает и достигает максимума при 
. Значение tm находится из условия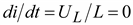 
. В интервале времени tm < t < ∞ ток по абсолютному значению убывает, стремясь к нулю.
Рассмотрим случай, когда корни характеристического уравнения вещественны и равны друг другу.
Это происходит при 
, т.е. при 
. В этом случае 
. При этом выражения для тока и напряжения становятся неопределенными из-за равенства нулю числителя и знаменателя. Раскроем эти неопределенности по правилу Лопиталя, считая, что p1 – переменная и стремится к 
. Для тока получим
9) При каких корнях характеристического уравнения в цепи R-L-C возникает колебательный разряд конденсатора? Написать уравнения для uC(t), i(t), uL(t) при колебательном разряде конденсатора. Привести графики этих величин.
Пусть корни характеристического уравнения являются комплексными. Это имеет место при условии 
, т.е. при 
. Обозначим 
. Тогда корни характеристического уравнения запишутся:
, (9.43)
где 
. Угол Q лежит в пределах 
, так как 
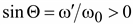и 
.
Переходный ток
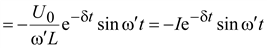
Кривая тока i подобна кривой Ri. Процесс в данном случае является колебательным. Ток и напряжение на всех участках периодически меняют знак. Амплитуда колебаний убывает по экспоненциальному закону, в цепи совершаются затухающие колебания. Угловая частота этих колебаний
.
10) Что такое логарифмический декремент колебания?
Логарифмический декремент колебаний — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону:
Логарифмический декремент колебаний
;
11) Что такое критическое сопротивление цепи R-L-C? Что такое критический режим цепи R-L-C?
При соотношении параметров контура из конденсатора, катушки и резистора
,
где RКР - критическое сопротивление резистора R, корни характеристического уравнения контура вещественные, равные и отрицательные:
p1 = p2 = p = -R / (2L).
Переходный процесс получается апериодическим, но граничным с колебательным процессом. Переходный ток и переходное напряжение в этом случае имеют вид:
uC = (A1 + A2 t) ept;
.
R2 = 4L/C
Данный режим можно назвать граничным или критическим. Здесь оба корня характеристического уравнения совпадают, но при этом являются действительными и отрицательными. Общее решение уравнения выражается функцией.
Задание к выполнению работы
1. Собрать цепь (см. рисунок 5.1).
2. Установить значения Uвх, R и C согласно варианту (см. таблицу 5.1), R1=100-300 Ом.
3. На вход осциллографа подать напряжение с конденсатора.
4. Срисовать в масштабе полученную кривую uC(t).
Рисунок 5.1
Рисунок 5.2
Таблица 5.1
| № варианта | Uвх,В | R,Ом | С,мкФ |
Таблица 5.2
| № варианта | Uвх,В | R,Ом | С,мкФ |
Таблица 5.3
| № варианта | R, Ом | L, мГн | С, мкФ |
5.2.5 Изменить согласно варианту один из параметров цепи (см. таблицу 5.2), срисовать в масштабе новую кривую uC(t), совместив ее с первой. Сравнить полученные кривые.
5.2.6 Собрать цепь (см. рисунок 5.2)
5.2.7 Установить значения R, L и C согласно варианту (см. таблицу 5.3). Измерить сопротивление катушки Rк. Напряжение на входе Uвх установить порядка 20-30В, R1=50-300 Ом.
5.2.8 На вход осциллографа подать напряжение с конденсатора.
5.2.9 Исследовать колебательный разряд конденсатора, срисовать в масштабе осциллограмму напряжения uC(t).
5.2.10 Добиться критического режима в цепи, меняя сопротивление R. Записать величину полученного сопротивления Rкр (эксп). Учесть сопротивление катушки Rк. Зарисовать полученную осциллограмму напряжения uC(t).
5.2.11 Увеличить сопротивление цепи R в 2 раза по сравнению с критическим. Зарисовать осциллограмму напряжения uC(t) при апериодическом разряде конденсатора.
