Таблица 1
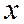
| 
| 
| ... | 
|

| 
| 
| ... | 
|



Найдем частные производные по параметрам
 ,
, 
Составим систему уравнений вида (1.4)
 ,
,

После алгебраических преобразований перепишем систему в виде


Варианты заданий
| N | ||||||||||||||||||||||
| xi | ||||||||||||||||||||||
| yi | 11.5 | 6.5 | 5.5 | 6.5 |
| N | |||||||||||||||||||||
| xi | |||||||||||||||||||||
| yi | 6.5 | 6.5 |
Пример выполнения задания
Ручной счет (n=4)
| i | 
| 
| 
| 
|
| 2.5 | ||||

| 10.5 |
30a+10b=29
10a+4b=10.5
det=30*4-10*10=20
a=(29*4-10.5*10)/20=0,55, b=(30*10.5-10*29)/20=1.25
y=0.55x+1.25
Выполнение работы на ЭВМ.
Для выполнения создается М-файл. Ниже приведен текст М-файла.
f_id=fopen('inpdata.dat','rt');
x=str2num(fgetl(f_id));
y=str2num(fgetl(f_id));
n=length(x);
fprintf('\n Данные эксперимента:')
fprintf('\n x:'); fprintf('%5.1f ',x);
fprintf('\n y:'); fprintf('%5.1f ',y);
s=0; sx=0; sy=0; sxx=0; sxy=0;
for i=1:n
sx=sx+x(i);
sy=sy+y(i);
sxx=sxx+x(i)*x(i);
sxy=sxy+x(i)*y(i);
end
a=(n*sxy-sx*sy)/(n*sxx-sx*sx);
b=(sy-a*sx)/n;
for i=1:n
s=s+(a*x(i)+b-y(i))^2;
end
fprintf('\n МНК-прямая: \n y=%8.4f ',a);
fprintf('*x+%8.4f ',b);
fprintf(' s=%8.4f \n',s);
Результаты расчета в командном окне при n=12:
Данные эксперимента:
x: 1.0 2.0 3.0 4.0 4.0 5.0 3.0 6.0 10.0 8.0 9.0 7.0
y: 2.0 2.5 2.0 4.0 4.5 5.0 4.0 5.0 9.0 7.0 8.0 7.0
МНК-прямая:
y= 0.7918*x+ 0.9089
s= 3.2807
Следует пояснить, что в представленной программе (а также в последующих программах, относящихся к данной лабораторной работе) ввод данных (массивов x и y) выполняется из файла из файла inpdata.dat. Использованная функция str2num позволяет преобразовать числовые данные, представленные элементами символьного массива, который был считан из файла inpdata.dat. Содержимое указанного файла для рассматриваемого примера имеет вид:
1.0 2.0 3.0 4.0 4.0 5.0 3.0 6.0 10.0 8.0 9.0 7.0
2.0 2.5 2.0 4.0 4.5 5.0 4.0 5.0 9.0 7.0 8.0 7.0
Альтернативный вариант текста программы
Для построения аппроксимирующего полинома заданной степени, приближающего функцию одной переменной, заданную соответствующими массивами значений, в системе MATLAB может использоваться функция polifit, реализующая метод наименьших квадратов. Имеем:
q=polifit(x,y,n),
где y – вектор значений функции, x – вектор значений аргумента, n – порядок аппроксимирующего полинома, p – полученный в результате вектор коэффициентов аппроксимирующего полинома длиной n+1.
Пусть имеется массив значений аргументов
x=[1 2 3 4 4 5 3 6 10 8 9 7];
и массив соответствующих им значений измеряемой величины:
y=[2 2.5 2 4 4.5 5 4 5 9 7 8 7];
Найдем аппроксимирующий полином при n=1, n=2, n=3
>> x=[1 2 3 4 4 5 3 6 10 8 9 7];
>> y=[2 2.5 2 4 4.5 5 4 5 9 7 8 7];
>> p1=polifit(x,y,1)
p1=
0.7918 0.9089
>> p2=polifit(x,y,2)
p2=
0.0107 0.6724 1.1593
>> p3=polifit(x,y,3)
p3=
-0.0017 0.0392 0.5421 1.3132
f_id=fopen('inpdata.dat','rt');
x=str2num(fgetl(f_id));
y=str2num(fgetl(f_id));
n=length(x);
fprintf('\n Данные эксперимента:')
fprintf('\n x:'); fprintf('%5.1f ',x);
fprintf('\n y:'); fprintf('%5.1f ',y);
p1=polyfit(x,y,1);
a=p1(1); b=p1(2);
s=0;
for i=1:n
s=s+(a*x(i)+b-y(i))^2;
end
fprintf('\n МНК-прямая: \n y=%8.4f ',a);
fprintf('*x+%8.4f ',b);
fprintf(' s=%8.4f \n',s);
y1=polyval(p1,x);
plot(x,y,'r*',x,y1);
title('График оптимальной прямой и экспериментальные точки');
grid on
xlabel('x');ylabel('y');
Рис. Пример построения оптимальной прямой по методу наименьших квадратов.
По тексту программы необходимо сделать ряд пояснений и замечаний.
1. Для построения аппроксимирующего полинома заданной степени, приближающего функцию одной переменной, заданную соответствующими массивами значений, в системе MATLAB может использоваться функция polyfit, реализующая метод наименьших квадратов. Имеем: q=polyfit(x,y,n), где y – вектор значений функции; x – вектор значений аргумента; n – порядок аппроксимирующего полинома; p – полученный в результате вектор коэффициентов аппроксимирующего полинома длиной n+1.
2. Альтернативный вариант программы предусматривает, как видно, не только определение уравнения оптимальной прямой по методу наименьших квадратов, но и построение этой прямой, а также соответствующих экспериментальных точек.






