Поверхностные волны (волны Рэлея)

На свободной поверхности тела могут возникать поверхностные волны, которые также называют волнами Релея (рис. 3.11). Они представляют собой комбинацию продольных и поперечных волн. В поверхностной волне колебания частиц происходят по эллиптической траектории, при этом большая ось эллипса перпендикулярна поверхности.

Рис.3.11. Распространение и колебания частиц в поверхностной волне.

 

Скорость их распространения равна

(15)

при υ = 0,3 .

Поверхностная волна локализована в тонком поверхностном слое толщиной 1,5λs и благодаря этому распространяется на большие расстояния вдоль поверхности твердого тела. Её амплитуда убывает по закону вследствие дифракционного расхождения пучка, тогда как . Коэффициент ослабления релеевской волны δs есть линейная комбинация аналогичных коэффициентов ослабления продольной () и поперечной (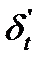) волн и записывается в виде:

δs = A · + B (16)

А и В – постоянные коэффициенты зависящие от υ. Если принять υ≈0,3, то δs = 0,89 . Видно, что δs в основном определяется ослаблением поперечных волн. Поверхностные волны могут распространяться не только по плоской, но и по искривленной (выпуклой или вогнутой) поверхностям (рис. 3.12).

Рис.3.12.Распространение поверхностной волны по изогнутой поверхности.

 

В отличие от плоской поверхности на выпуклой поверхности волна будет распространяться с несколько большей скоростью, но затухание такое же, как на плоской поверхности. На вогнутой поверхности релеевская волна будет распространяться с большим затуханием, которое обусловлено радиальным излучением энергии в среду. Величина дополнительного затухания определяется соотношением R/λs. При R/λs ≈ 5 затухание весьма значительно по сравнению с плоской поверхностью, и только при R/λs ≥ 50 оно примерно такое же, как и на плоскости. Фазовая скорость поверхностных волн на криволинейных поверхностях определяется выражением

(17)

где - скорость релеевских волн на плоскости;

γ – показатель криволинейности пропорционален 1/R.

Если две плоскости образуют двугранный угол, то релеевская волна дойдя до ребра, частично отразится, частично перейдет на другую плоскость, а частично трансформируется в другие типы волн (продольные и поперечные).

Соотношение между коэффициентами отражения и прохождения зависит от угла θ. При θ < 900 имеет место осцилляции значений коэффициентов R и D, а при θ ≥ 1100 наблюдается монотонное уменьшение R и увеличение D.

Рис.3.13. Прохождение и отражение поверхностной волны от угла (при θ= 900, R = 37 %, D =51%, ≈ 12%).

 

Значение R и D существенно зависит от закругления между гранями клина. При r/λs>1,7 значение закругления не сказывается.

При распространении релеевской волны вдоль поверхности, на которой имеются различные дефекты, происходит рассеяние релеевской волны, а также возникают трансформированные продольные и поперечные волны, распространяющиеся вглубь среды. Значение рассеянной энергии будет зависеть от вида дефекта и его линейных размеров высоты (в) и глубины залегания (h). Округлый дефект значительно хуже отражает S волны.

Волна Лэмба

При наклонном падении волны на пластину соизмеримой с длиной волны, вследствие сложения падающей волны с многократно отраженными волнами внутри пластины, возникают резонансные явления, сопровождающиеся образованием стоячих волн (рис.3.14).

Рис.3.14. Распространение бегущих Cg и стоячих Cj волн в пластинах.

 

Взаимодействие стоячих и бегущих волн приводит к возникновению нормальных волн (волн Лэмба) с вертикальной поляризацией (рис.3.15).

Рис.3.15. Распространение и колебания частиц в нормальной симметричной (а) и ассиметричной (б) волнах.

 

Рассмотрим физику образования нормальных волн (рис.3.16).

Рис.3.16. Возникновение нормальных волн в жидком слое.

Пусть на жидкий слой толщиной h под углом β падает плоская гармоническая волна. Линия АД показывает фронт падающей волны. В результате ее преломления на границе, в слое возникает волна с фронтом СД, распространяющаяся под углом α и претерпевающая многократные отражения в слое. При определенном угле падения β волна, отраженная от нижней поверхности совпадает по фазе с прямой падающей волной. Угол, при котором наблюдается явление резонанса – совпадение по фазе падающей и отраженной волн будет равен: , где n - целое число; - длина волны в слое. Это соответствует условию образования волн Лэмба.

Различные типы волн, существующие при различных значениях n, называют модами нормальных волн. Волны с нечетным n называют симметричными волнами расширения-сжатия (т.к. движение частиц в них симметрично относительно оси пластины (рис.3.15а). Волны с четным n называют асимметричными (изгибающими волнами (рис.3.15б), т.к. в них движение частиц асимметрично относительно центральной плоскости пластин. Моды симметричных волн обозначают S0, S1, S2… асимметричных α0, α1, α3… Нулевыми индексами отмечены моды, которые при увеличении толщины пластины переходят в поверхностные волны.

При распространении нормальных волн пользуются понятием фазовой (Ср) и групповой (Су) скоростей, которые связаны между собой соотношением:

(18)

Фазовая скорость определяет скорость распространения волнового фронта. Она позволяет вычислить частоту f ультразвуковых (УЗ) колебаний и необходимый угол падения. Найдем выражение фазовой скорости (рис. 3.17).

Рис.3.17. Соотношение между объемной С2, групповой Сд и фазовой Ср скоростями в пластине.

 

Используя выражение , получим

(19)

Из последнего выражения следует, что фазовая скорость зависит от частоты УЗ колебаний и толщины слоя. При достижении условий, когда h/λ2=n (n=1,2,3 и т.д.), фазовая скорость стремится к бесконечности. При h/λ2 → ∞ из выражения следует, что фазовая скорость будет равна скорости обычной объемной волны С2.

Групповая скорость С д характеризует скорость распространения энергии волнового фронта (импульса) и численно равна

(20)

Из выражения видно, что С д никогда не обращается в бесконечность и при стремится к нулю, в то время как фазовая скорость Ср стремится к бесконечности при h/λ2 > 10; Cp ≈ С д.

Условия образования нормальных волн в твердой пластине усложняются из-за наличия в ней продольных и поперечных волн. При отражении эти волны частично трансформируются друг в друга, а фаза волны при отражении меняется на число, не кратное π.

На рис. 3.18 показаны дисперсионные кривые для пластины из стали (ν≈0,3).

Рис.3.18. Дисперсионные кривые для волн Лэмба в твердом теле:

Cℓ, Ct, Cs – скорости распространения соответственно продольных, поперечных и поверхностных волн;

а0, а1, а2 – асимметричные волны; S0, S1, S2 – симметричные волны.

Головные волны

В реальных условиях УЗ контроля наклонным преобразователем фронт УЗ волны излучающего пьезоэлемента имеет неплоскую форму. От излучателя, ось которого ориентирована под 1-м критическим углом к границе раздела, на границу падают также продольные волны с углами несколько меньше и несколько больше 1-го критического. При этом в стали возбуждается несколько типов УЗ волн.

Вдоль поверхности распространяется неоднородная продольно-поверхностная волна. Эту волну, состоящую из поверхностной и объемной компонент, называют также вытекающей или ползучей. Частицы в этой волне движутся по траекториям в виде эллипсов, близких к окружностям. Фазовая скорость вытекающей волны Сф незначительно превышает скорость продольной волны (для стали Сф 1,04 С1). Эти волны существуют на глубине, примерно равной длине волны, и быстро затухают при распространении: амплитуда волны затухает в 2,7 раза на расстоянии 1,75λ вдоль поверхности. Ослабление связано с тем, что в каждой точке границы раздела генерируются поперечные волны под углом αt2, равным третьему критическому углу, называемые боковыми волнами. Этот угол определяется из соотношения

(21)

Для стали αt2 = 33,50.

Кроме, вытекающей, возбуждается также головная волна, получившая широкое применение в практике УЗ-контроля. Головной называют продольно-подповерхностную волну, возбуждаемую при падении УЗ-пучка на границу раздела под углом, близким к первому критическому. Скорость этой волны равна скорости продольной волны. Своего амплитудного значения головная волна достигает под поверхностью вдоль луча с углом ввода 780. Головная волна, как и вытекающая, порождает боковые поперечные волны под третьим критическим углом к границе раздела. Одновременно с возбуждением продольно-поверхностной волны образуется и обратная продольно-поверхностная волна – распространение упругого возмущения в сторону, противоположную прямому излучению. Ее амплитуда примерно в 100 раз меньше амплитуды прямой волны.

Головная волна нечувствительна к неровностям поверхности и реагирует лишь на дефекты, залегающие под поверхностью. Ослабление амплитуды продольно-подповерхностной волны вдоль луча любого направления происходит как в обычной объемной продольной волне, то есть пропорционально 1/r.

 

ЛЕКЦИЯ №4. ИСТОЧНИКИ УЛЬТРАЗВУКОВЫХ ВОЛН

Современные дефектоскописты имеют в своем распоряжении большой ассортимент различных источников ультразвуковых колебаний, основанных на различных физических принципах. Это пьезоэлектрические преобразователи (ПЭП), электромагнитно акустические преобразователи (ЭМАП), лазерные источники.